Разложение несимметричной системы полных векторов на симметричные составляющие.

Рисунок 2. 3. Исходная трехвекторная система

1. Каждый из векторов исходной системы представим суммами векторов ПП, ОП и НП А = А1 + А2 +А0   В = В1 + В2 +В0   С = С1 + С2 +С0 К этому добавим два равенства А0 = В0 и С0 =А0

Имеем исходную несимметричную систему полных векторов А, В, С (рисунок 2. 3).

 

2. Используя операторы а и   а ² запишем

А =                    = А₁  + А₂  + А₀

 

В = В₁ + В₂ +В₀     = А₁· а ² + А₂ · а + А₀                                (2. 7)

 

С = С₁ + С₂ +С₀     = А₁· а   + А₂   а ² + А₀

 

3. Сложим левые и правые части полученных уравнений

 

   А + В + С = 3 А₀ + А₁ ·(1 + а ² + а ) + А₂ ·(1 + а  + а ² )        (2. 8)

 

Здесь сумма операторов в скобках равна нулю, то есть (1+ а ²+ а )=0, а также (1+ а + а ² ) = 0.

Следовательно, составляющие НП определяются из выражения

 

             - векторы НП равны      (2. 9)

одной трети геометрической суммы полных исходных векторов.

    4. Умножив уравнение В = А₁· а ² + А₂ · а + А₀ на оператор а, а уравнение С = А₁ · а + А₂ · а ² + А₀ на оператор а ², уравнения (2. 7) запишем в виде

 

    А = А₁ + А₂ + А₀      

 

В · а = А₁ · а ³ + А₂· а ² + А₀ · а                                            (2. 10)

 

С · а ² = А₁ · а ³   + А₂ · а ⁴ + А₀· а ²

    5. Сложим левые и правые части уравнений (2. 10)

 

    А + В · а + С · а ² = А₁ ·(1+ а ³+ а ³) + А₂ ·(1+ а ²+ а ⁴) + А₀ ·(1+ а + а ²).

 

    Здесь в скобках а ³ = 1, а ⁴ = а.   Поэтому

 

(1+ а ³+ а ³) = 3, (1+ а ²+ а ⁴) =0, (1+ а + а ²) = 0.

 

В результате имеем

 

А + В · а + С · а ² = А₁ · 3. Отсюда

 

                     (2. 11)

 

Аналогично, умножив уравнение В  = А₁· а ² + А₂· а + А₀ на оператор а ²,  а уравнение С = А₁ · а + А₂ · а ² + А₀ на оператор а, получим третье уравнение разложения

 

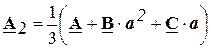                  (2. 12)

	В качестве примера, имея исходную несимметричную систему полных векторов А , В,  С (рисунок 2. 4), найдем вектор А1 (ПП), воспользовавшись выражением (2. 11). Чтобы получить слагаемые данного выражения полный вектор В повернем на 120º против часовой стрелки, полный вектор С повернем против часовой стрелки на 240º. Геометрическая сумма векторов А + В ·а+ С ·а2 равна утроенному значение вектор ПП А1

 

        

 

 

 

 

Аналогично найдем векторы А₂ и А₀, используя выражения (2. 12)  и  (2. 9).

 

 

3А0

3А2

А

С

В

А

В

В

С

С

С·а

В·а2

       а)                                                                                      б)

	Рисунок 2. 5 Определение векторов А2 (ОП) и А0 НП

 

 

В конечном виде формулы разложения несимметричной системы трех векторов на симметричные составляющие ПП, ОП и НП имеют вид:

 

   

 

         (2. 13)

 

    

 

                  А₀= В₀= С₀ = ( А+ В +С )

 

Есть несколько приемов графического разложения несимметричной системы трех векторов на симметричные составляющие ПП, ОП, НП. Ниже приводится один из них, именно тот, который находит широкое применение в релейной защите.

Пусть в качестве примера имеем исходную несимметричную систему трех векторов А+ В +С (рисунок 2. 6).

Обведем концы фазных векторов линейным треугольником. Получим три линейных вектора АВ = А - В; ВС = В - С; СА = С - А.

Из рисунка 2. 6 видно, что А = В + АВ, а С = В - ВС. Если подставить в формулы разложения (2. 13) для А₁ и А₂  два последних выражения, то получим:

	Рисунок 2. 6 Разложение  исходной трехвекторной системы на составляющие ПП и ОП

 

 

Чтобы получить вектор ВС· а ², необходимо вектор ВС развернуть на 240º против часовой стрелки. Принесем вектор ВС· а ² своим  началом в точку в. Тогда геометрическая разность векторов АВ - ВС· а ² будет являться утроенным вектором прямой последовательности. Определим на векторной диаграмме вектор А₁ как одну треть от полученной разности векторов (АВ - ВС· а ²). Направление вектора ПП А₁ от точки Р к точке а.

Для определения вектора ОП А₂ поступим аналогично. В формулу разложения для А₂ также вместо вектора А подставим (В + АВ), а вместо вектора С – ( В – ВС).

Получим

 

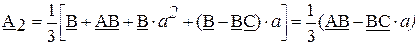           (2. 15)

 

Вектор, лежащий между концами векторов АВ и ВС· а , то есть от точки R до точки а, представляет собой утроенный вектор ОП 3А₂. Вектор ОП А₂ во-первых, равен одной трети полученной геометрической разности (АВ - ВС · а ), во-вторых, он направлен от вспомогательной точки R к концу вектора АВ, то есть к точке а.

 

 

Возвращаясь к рисунку 2. 6, следует отметить, что треугольники сРв и сRв (назовем их вспомогательными) являются равносторонними. Отстояние вспомогательных точек Р и R от конца вектора АВ определяет длины векторов 3А₁ и 3А₂.

Алгоритм поиска (построения) векторов ПП и ОП весьма прост. Рассмотрим его на конкретном примере.

Пусть имеем исходную несимметричную трехвекторную систему А, В, С (рисунок 2. 8). Задача: определить векторы ПП и ОП, входящие в состав полных векторов.

1. Изображаем исходную несимметричную систему полных векторов А, В, С.

2. Обводим концы фазных векторов линейным треугольником.

3. Выбираем любой из трех линейный вектор, например, ВС и делим его на две равные части.

4. Через середину вектора ВС проводим перпендикуляр для построения вспомогательных треугольников и точек Р и R.

5. Строим два равносторонних треугольника сРв и сRв.

6. Из вершин треугольников (из точек Р и R  к концу вектора АВ проводим векторы 3А₁ и 3А₂.

 

 

	Рисунок 2. 8. Разложение полных векторов несимметричной трехвекторной системы на составляющие ПП и ОП

 

 

7. Находим векторы А₁ и А₂ и достраиваем недостающие векторы В₁, С₁ и В₂, С₂.  

Построение различных исходных несимметричных систем, разложение их на составляющие ПП и ОП и их анализ приводят к следующим важным выводам:

1) значения составляющих ПП и ОП однозначно определяются линейными векторами исследуемых систем, то есть конфигурацией линейных треугольников и не зависят от взаимного расположения и значений фазных векторов;

 

 

       а)                                       б)                                       в)

	Рисунок 2. 9. Различные несимметричные трехвекторные системы

 

Несимметричные системы фазных векторов, представленные на рисунке 2. 9, имеют одинаковые линейные векторы (их линейные треугольные равноподобны) и соответственно этому они имеют одинаковые составляющие ПП и одинаковые составляющие ОП;

    2) в случаях, когда система линейных векторов оказывается симметричной, то есть когда линейный треугольник является равносторонним, как показано на рисунке 2. 10, полные векторы исходной несимметричных системы не содержат составляющих ОП; если и фазные векторы А, В, С, и линейные векторы АВ, СА, ВС представляют собой симметричные системы (рисунок 2. 10, а), то в составе полных фазных векторов содержатся только составляющие ПП. Это нетрудно доказать разложением на составляющие ПП и ОП трехфазных систем, приведенных на рисунке 2. 10.

 

 

                              а)                                                               б)

 

       На рисунке 2. 10 вспомогательная точка R совпадает с концом линейного вектора АВ, что указывает на равенство нулю составляющих ОП.

    На рисунке 2. 10, б) приведена исходная несимметричная система фазных векторов А, В, С, имеющая симметричную систему линейных векторов АВ, СА, ВС. Несмотря на несимметрию фазных векторов в них нет составляющих ОП. Здесь однако, наряду с составляющими ПП имеют место составляющие НП. На данном обстоятельстве следует остановиться подробнее.

    Рассмотрим два способа графического нахождения составляющих НП.

       Первый способ основан на построении векторной диаграммы, используя выражение (2. 9) .

 

 

Подставим их в формулу разложения для А₀

 

. (2. 16)

 

Построим вектор (АВ – ВС), который на рисунке изображается диагональю МN конец вектора МN лежит в точке N.     Найдем на рисунке 2. 12 вектор А0. Для этого согласно выражению (2. 16) отделим одну треть вектора МN, получим точку О'. Также, согласно выражению (2. 16) прибавим к вектору МО' вектор В. В результате получим вектор А0

На основании этого выражения осуществим построение вектора А₀ для произвольной несимметричной системы фазных векторов А, В, С (рисунок 2. 12). Соединим в концы фазных векторов, - получим треугольник КМL, стороны которого образуют линейные векторы АВ, ВС и СА.

 

На практике пользуются более простым алгоритмом построения составляющих НП, который полностью базируется на приведенных выше рассуждениях.

Пусть имеем ту же несимметричную трехвекторную систему полных векторов А, В, С (рисунок 2. 13).

1. Концы фазных векторов обведем линейным треугольником.

2.

3. Из вершин линейного треугольника проведем медианы, которые, пересекаясь, дадут точку О'.     4. Соединим исходную точку О с точкой пересечения медиан, - мы получим вектор А0. Вектор А0 направлен от точки О к точке О'. Векторы В0 и С0 на приведенной векторной диаграмме расположены также как и А0 между точками О и О'.

Каждую сторону треугольника разделим на две равные части.

	Рисунок 2. 13. Векторная диаграмма для нахождения составляющих НП

 

Точку О' (точку пересечения медиан в линейном треугольнике) называют центром тяжести линейного треугольника.

1. Если точка О (начало фазных векторов А, В, С) совпадает с центром тяжести треугольника линейных векторов (рисунок 2. 14), то в полных фазных векторах исследуемой трехфазной системы не содержатся составляющие НП. По известной физической аналогии со свойствами центра тяжести треугольника такую систему фазных векторов называют несимметричной но уравновешенной.

Из приведенного выше можно сделать следующие выводы.

 

2. Положение точки О' (точки пересечения медиан) однозначно определяется взаимным расположением линейных векторов, то есть конфигурацией линейного треугольника (рисунок 2. 15).

 

 

Рисунок 2. 15. Исходные трехвекторные системы с различной степенью ассиметрии.

а)                                       б)                           г)                           в)

 

Рассмотрим несколько примеров разложения на симметричные составляющие исходной несимметричной трехфазной системы векторов А, В, С (рисунки 2. 16, 2. 17, 2. 18, 2. 19)

1. Изобразим исходную несимметричную систему полных векторов А, В, С (рисунок 2. 16).

2. Концы векторов А, В, С обведем линейный треугольником.

3. Разделим вектор ВС на две равные части, проведем через середину перпендикулярную к нему линию.

4. Построим на линии СВ два равносторонних вспомогательных треугольника сРв и сRв.

5. Полученные вспомогательные точки Р и R соединим с концом вектором вектора АВ (от есть с точкой а).

 

 

В качестве второго примера возьмем несколько иную систему исходных фазных векторов (рисунок 2. 17) и проделаем те же операции (пункты 1 ÷ 8).

Как следует из векторной диаграммы на рисунке 2. 17, геометрические суммы последовательностей дают полные векторы исходной несимметричной системы

 

А = А₁+ А₂+ А₀; В = В₁+ В₂+ В₀; С = С₁+ С₂+ С₀.

 

	Рисунок 2. 17. Векторная диаграмма полных векторов исходной трехвектроной системы и векторов симметричных составляющих ПП, ОП, НП.

 

Рассмотрим еще два примера разложения полных векторов на симметричные составляющие.

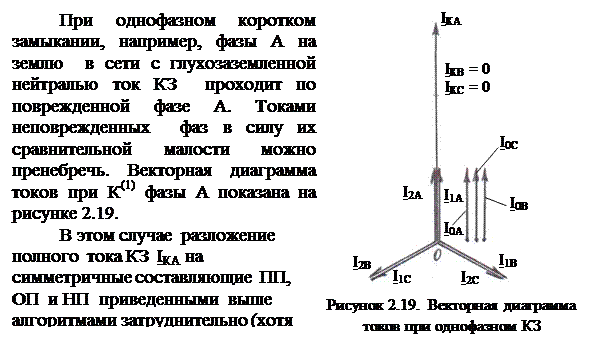
Известно, что при двухфазном КЗ, например, фаз В и С токи короткого замыкания проходят по поврежденным фазам. Током в неповрежденной фазе А для простоты рассуждений и расчетов пренебрегают.

 

 

Поэтому для определения составляющих НП воспользуемся формулой разложения (2. 9). В нашем случае В = - С.

Следовательно,

 

 

 

Воспользуемся формулами разложения (2. 13)

 

       ,

 

       ,

 

       .

 

Проверка правильности разложения показывает

 

      

 

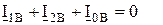       и

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: