Общие выводы. 3.4 Двухфазное КЗ на землю в одной точке
Общие выводы
1. Токи и фазные напряжения при К(1) образуют несимметричные и неуравновешенные системы полных векторов, что свидетельствует о наличии в них составляющих ПП, ОП, НП.
2. В отличие от двухфазного КЗ при К(1) междуфазные напряжения в точке К (тем более на шинах подстанции) больше нуля.
3. Однофазное КЗ является менее опасным повреждением с точки зрения устойчивости работы ЭЭС и потребителей.
4.  Сравнивая векторные диаграммы токов ОП и напряжений ОП, приходим к однозначному выводу: фазный ток ОП
Сравнивая векторные диаграммы токов ОП и напряжений ОП, приходим к однозначному выводу: фазный ток ОП 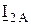 опережает напряжение ОП одноименной фазы
опережает напряжение ОП одноименной фазы  на угол 1100 ÷ 1200. Данный угол учитывается при конструировании и расчётах реле мощности обратной последовательности.
на угол 1100 ÷ 1200. Данный угол учитывается при конструировании и расчётах реле мощности обратной последовательности.
3. 4 Двухфазное КЗ на землю в одной точке
Этот вид КЗ (К(1. 1)) также как и К(1) может возникать в сетях с глухозаземлёнными нейтралями.

Этот вид сложного для анализа КЗ может быть исследован как наложение на двухфазное (ВС) КЗ, рассмотренное в пункте 3. 2, однофазных коротких замыканий фаз В и С.
В неповреждённой фазе А ток отсутствует. Напряжение фазы А в любой точке линии можно считать равным  .
.
Под действием междуфазной ЭДС 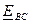 по фазам В и С проходит ток двухфазного КЗ
по фазам В и С проходит ток двухфазного КЗ  и
и  . Кроме того под действием фазных ЭДС
. Кроме того под действием фазных ЭДС  и
и  по повреждённым фазам проходят токи однофазных КЗ
по повреждённым фазам проходят токи однофазных КЗ  и
и  .
.
Векторная диаграмма токов при К(1. 1) для точки К приведена на рисунке 3. 16.
Ток двухфазного КЗ в фазе В отстаёт от ЭДС 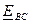 на угол
на угол  . Ток двухфазного КЗ в фазе С
. Ток двухфазного КЗ в фазе С  ему встречен.
ему встречен.
Ток однофазного КЗ в фазе В  отстаёт от своей ЭДС
отстаёт от своей ЭДС  (если рассматривать удалённое КЗ) на угол
(если рассматривать удалённое КЗ) на угол 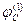 .
.
Ток однофазного КЗ в фазе С  отстаёт от своей ЭДС
отстаёт от своей ЭДС  также на угол
также на угол 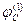 .
.
Геометрическая сумма токов КЗ  и
и  даёт полный ток двухфазного КЗ на землю в точке К, т. е.
даёт полный ток двухфазного КЗ на землю в точке К, т. е.
 , а также
, а также 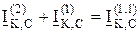
Из рисунка 3. 16 следует, что при К
(1. 1) в отличие от К
(2) токи КЗ

и

не являются чисто противофазными. Угол сдвига фаз между этими токами в силу ряда причин может изменяться от 180
0 до 140
0 
150
0.

| | | | | | | | | | | | | |
| | |
| | | |
|
|
| |  |
| | |
|
|
| |  |
| | |  |
|
|
| | Рисунок 3. 17. Разложение на симметричные составляющие токов КЗ при К(1. 1).
| |
Разложим на симметричные составляющие полные токи К(1. 1). Чтобы не загромождать рисунок 3. 16 разложением на симметричные составляющие, выберем из рисунка 3. 16 векторы  и
и  и для большей наглядности уменьшим между ними угол сдвига фаз, сохраняя величины векторов.
и для большей наглядности уменьшим между ними угол сдвига фаз, сохраняя величины векторов.
Из рисунка 3. 17 следует, что при двухфазном замыкании на землю в составе полных токов есть составляющие ПП, ОП и НП. Значения токов 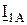 ,
,  ,
, 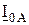 (и других) во многом зависят от ряда факторов и могут быть непостоянными в процессе эксплуатации ЛЭП. Это создаёт дополнительные трудности в анализе работы релейной защиты и в определении эффективности её функционирования.
(и других) во многом зависят от ряда факторов и могут быть непостоянными в процессе эксплуатации ЛЭП. Это создаёт дополнительные трудности в анализе работы релейной защиты и в определении эффективности её функционирования.
На рисунке 3. 18 приведена векторная диаграмма полного напряжения  для точки К и его симметричных составляющих. В точке К (рисунок 3. 15) напряжение фазы А равно
для точки К и его симметричных составляющих. В точке К (рисунок 3. 15) напряжение фазы А равно  . Напряжение повреждённых фаз в точке К равны нулю.
. Напряжение повреждённых фаз в точке К равны нулю.
Междуфазные напряжения К(1. 1) в точке К уменьшаются до фазного напряжения
 ;
; 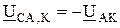 .
.
В точке К линейный треугольник “стягивается” в линию, соответствующую вектору  .
.
Фазное напряжение неповреждённой фазы  содержит все три составляющие ПП, ОП и НП. По модулю все векторы симметричных составляющих равны между собой и равны
содержит все три составляющие ПП, ОП и НП. По модулю все векторы симметричных составляющих равны между собой и равны  .
.
В месте установки защиты (на шинах подстанции) величины остаточных фазных напряжений  и
и  отличны от нуля. Чем дальше отстоит точка К от шин подстанции, тем больше остаточные напряжения
отличны от нуля. Чем дальше отстоит точка К от шин подстанции, тем больше остаточные напряжения  и
и  .
.
При этом возрастают и междуфазные напряжения.
Построим векторные диаграммы токов и напряжений для точки 1 (на шинах подстанции).
Векторы токов  и
и  остаются прежними, как на рисунке 3. 16.
остаются прежними, как на рисунке 3. 16.
Напряжение на шине А подстанции 1 равно напряжению фазы А в точке К, т. е. 

точки P и R
| Рисунок 3. 19. Векторная диаграмма полных остаточных напряжений на шинах подстанции и их симметричных составляющих
| |
Треугольник линейных напряжений сва является несимметричным и неуравновешенным, что свидетельствует о наличии в составе исходных фазных напряжений  ,
,  ,
,  составляющих ПП, ОП и НП.
составляющих ПП, ОП и НП.
Векторная диаграмма на рисунке 3. 19 построена с некоторыми допущениями, которые не оказывают заметного влияния на истинность хода рассуждений.
Сравнивая и анализируя векторные диаграммы на рисунках 3. 16; 3. 17; 3. 18; 3. 19 можно прийти к следующим выводам:
1) как и в случае однофазного КЗ, при К(1. 1) по мере удаления точки КЗ от шин подстанции возрастают фазные и междуфазные напряжения на шинах;
2) при удалённых КЗ значения напряжений ОП и НП уменьшаются, а напряжения ПП возрастают;
3) из-за резкого снижения напряжений в месте КЗ этот вид повреждения после К(3) является наиболее тяжелым для устойчивости работы ЭЭС и потребителей;
4) при К(1. 1) угол сдвига фаз между током ОП  и напряжением ОП одноимённой фазы
и напряжением ОП одноимённой фазы  может отличаться от значения 1200
может отличаться от значения 1200  1100, как это наблюдается при К(1) и К(2).
1100, как это наблюдается при К(1) и К(2).
Воспользуйтесь поиском по сайту:


 Сравнивая векторные диаграммы токов ОП и напряжений ОП, приходим к однозначному выводу: фазный ток ОП
Сравнивая векторные диаграммы токов ОП и напряжений ОП, приходим к однозначному выводу: фазный ток ОП 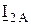 опережает напряжение ОП одноименной фазы
опережает напряжение ОП одноименной фазы  на угол 1100 ÷ 1200. Данный угол учитывается при конструировании и расчётах реле мощности обратной последовательности.
на угол 1100 ÷ 1200. Данный угол учитывается при конструировании и расчётах реле мощности обратной последовательности. 
 .
. 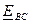 по фазам В и С проходит ток двухфазного КЗ
по фазам В и С проходит ток двухфазного КЗ  и
и  . Кроме того под действием фазных ЭДС
. Кроме того под действием фазных ЭДС  и
и  по повреждённым фазам проходят токи однофазных КЗ
по повреждённым фазам проходят токи однофазных КЗ  и
и  .
. 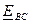 на угол
на угол  . Ток двухфазного КЗ в фазе С
. Ток двухфазного КЗ в фазе С  ему встречен.
ему встречен.  отстаёт от своей ЭДС
отстаёт от своей ЭДС  (если рассматривать удалённое КЗ) на угол
(если рассматривать удалённое КЗ) на угол 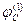 .
.  отстаёт от своей ЭДС
отстаёт от своей ЭДС  также на угол
также на угол 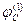 .
.  и
и  даёт полный ток двухфазного КЗ на землю в точке К, т. е.
даёт полный ток двухфазного КЗ на землю в точке К, т. е.  , а также
, а также 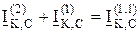

 и
и  не являются чисто противофазными. Угол сдвига фаз между этими токами в силу ряда причин может изменяться от 1800 до 1400
не являются чисто противофазными. Угол сдвига фаз между этими токами в силу ряда причин может изменяться от 1800 до 1400  1500.
1500.




 и
и  и для большей наглядности уменьшим между ними угол сдвига фаз, сохраняя величины векторов.
и для большей наглядности уменьшим между ними угол сдвига фаз, сохраняя величины векторов. 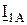 ,
,  ,
, 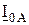 (и других) во многом зависят от ряда факторов и могут быть непостоянными в процессе эксплуатации ЛЭП. Это создаёт дополнительные трудности в анализе работы релейной защиты и в определении эффективности её функционирования.
(и других) во многом зависят от ряда факторов и могут быть непостоянными в процессе эксплуатации ЛЭП. Это создаёт дополнительные трудности в анализе работы релейной защиты и в определении эффективности её функционирования.  для точки К и его симметричных составляющих. В точке К (рисунок 3. 15) напряжение фазы А равно
для точки К и его симметричных составляющих. В точке К (рисунок 3. 15) напряжение фазы А равно  . Напряжение повреждённых фаз в точке К равны нулю.
. Напряжение повреждённых фаз в точке К равны нулю.  ;
; 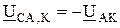 .
.  .
. 
 содержит все три составляющие ПП, ОП и НП. По модулю все векторы симметричных составляющих равны между собой и равны
содержит все три составляющие ПП, ОП и НП. По модулю все векторы симметричных составляющих равны между собой и равны  .
.  и
и  отличны от нуля. Чем дальше отстоит точка К от шин подстанции, тем больше остаточные напряжения
отличны от нуля. Чем дальше отстоит точка К от шин подстанции, тем больше остаточные напряжения  и
и  .
.  и
и  остаются прежними, как на рисунке 3. 16.
остаются прежними, как на рисунке 3. 16. 



 ,
,  ,
,  составляющих ПП, ОП и НП.
составляющих ПП, ОП и НП.  и напряжением ОП одноимённой фазы
и напряжением ОП одноимённой фазы  может отличаться от значения 1200
может отличаться от значения 1200  1100, как это наблюдается при К(1) и К(2).
1100, как это наблюдается при К(1) и К(2). 



















