 |
1. Метод конечных элементов (МКЭ).
|
|
|
|
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
1. Метод конечных элементов (МКЭ).
Из-за сложности и высоких затратах проведения экспериментов по деформированию металлов и сплавов необходимо обратиться к компьютерному моделированию, которое будет рассмотрено в следующем разделе. В большинстве видов компьютерного моделирования применяется метод конечных элементов (МКЭ). Это метод приближённого численного решения физических задач, который работает по принципу разбиения объекта на n-ое множество элементов и упрощения исследуемых функций поэлементно.
Перед изобретением метода конечных элементов были разнообразные методы строительной механики и механики деформируемого твёрдого тела, которые используют разбиение. Ещё Пуассон в начале XIX века предлагал рассматривать сплошную среду как систему конечных объёмов. Во второй половине XIX века были заложены основы анализа стержневых конструкций Д. Максвеллом, А. Кастильяно и другие, а в последующие годы уже были сформулированы метод сил, а затем и метод перемещений.
С 50-х годов XX века началось практическое применение ЭВМ в инженерных расчётах, что способствовало возникновению различных матричных методов анализа конструкций. Весомый вклад в развитие матричных методов строительной механики внесли Дж. Аргирис и другие, а также советские учёные.
В 1960 году Клаф впервые ввёл термин «конечные элементы».
Своему быстрому распространению и становлению в качестве ведущего метода решения физических задач этот метод обязан своим преимуществам, затмевающим другие методы, а именно:
1) объекты, задачи с которыми решаются, могут иметь различную форму и среду;
2) сами конечные элементы могут иметь различную форму;
|
|
|
3) объектами исследования этим методом могут быть однородные и неоднородные, изотропные и анизотропные;
4) можно производить решение стационарных и нестационарных задач;
5) можно производить решение контактных задач;
6) можно моделировать различные граничные условия;
7) для облегчения анализа связанных задач благодаря этому методу можно решать задачи на одной сетке конечных элементов;
8) для ускорения вычисления в его разрешающей системе есть разреженная симметричная матрица «жёсткости»;
На рисунке 16 показано, как деформируемое тело разбивается на конечные элементы, которые могут быть различных формы и размеров. После операции по разбивке создаётся сетка из границ элементов, а пересечения этих границ образуют узлы. На границах и внутри элементов могут быть созданы дополнительные узловые точки. Всё это образует конечно-элементную модель деформируемого тела. Дискретная модель должна хорошо покрывать область исследуемого объекта [35].
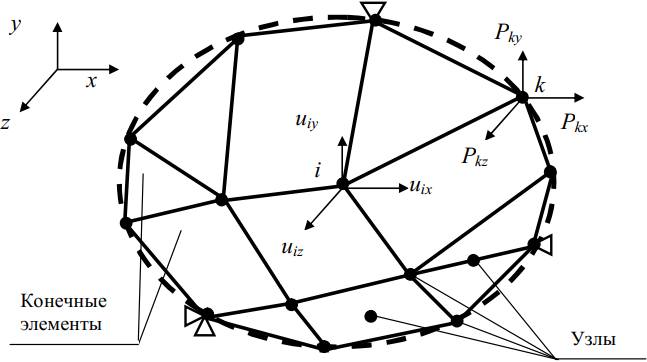
– Конечно-элементная модель
2. Препроцессор программы DEFORM.
Внешний вид препроцессора, запущенного в режиме помощника деформирования, несколько отличается от препроцессора обычного режима (рис. 3). Он также имеет главное меню и панели инструментов (панель работы с файлами и панель управления изображением), но в правой части находится дерево построения, облегчающее создание модели расчета.
Запускаем программный комплекс DEFORM-3D, затем создаем новую задачу. После чего появляется окно препроцессора, необходимого для создания, сбора или изменения данных, требуемых для проведения расчета и для создания файла базы данных для расчета (рис. 1. 2) [1].
Рассмотрим последовательность действий в препроцессоре DEFORM-3D.
Для начала заходим в параметры моделирования (Simulation Controls) и настраиваем процесс моделирования:
Во вкладке «Основное» задаем основные параметры моделирования под наш процесс (рис. 1. 3):
|
|
|
· устанавливаем единицы измерения СИ;
· выставляем тип моделирование Анализ Лагранжа (Lagrangian Incremental);
· выбираем режимы, которые нужно исследовать.
Во вкладке «Шаг» настраиваем параметры шага (рис. 1. 4):
· задаем номер начального шага;
· число шагов расчета;
· через сколько шагов сохранять результаты;
· выбираем главный инструмент;
· вводим время прохождения одного шага.
После настройки параметров симуляции процесса переходим к импортированию модели заготовки и инструмента. DEFORM-3D поддерживает файлы с расширением «. stl». Также можно создать модель и в самом модуле, но так как он имеет ограниченные возможности по созданию трехмерных моделей, удобнее будет выбрать вариант с импортированием модели. Строим заготовку небольших размеров и с простой геометрией, так как при увеличении объема детали увеличивается время расчета.
Вслед за импортированием модели заготовки во вкладке «Общее» выбираем тип исследуемого объекта «Пластичный», задаем начальную температуру и материал заготовки выбираем из библиотеки – Сталь 38ХМА (рис. 1. 5).
Затем заходим во вкладку «Сетка» и генерируем сетку. Сетку можно сгенерировать «Относительную» и «Абсолютную». Мы же выбираем сгенерировать как «Абсолютную» и выставляем такие параметры (рис. 1. 6).
Для более точных результатов исследования сгущаем сетку в зоне резания, т. е. уменьшаем размер конечных элементов (рис. 1. 7).
После чего заходим во вкладку граничных условий «Bdry. Cnd. ». Здесь мы фиксируем заготовку по трем координатам, задаем плоскость с которой будет сопряжен контакт инструмента с заготовкой и задаем плоскости в которых нас будет интересовать теплообмен с окружающей средой (рис. 1. 8).
Далее заходим во вкладку «Свойства»/«Деформационные» выбираем тип компенсации потери объема «Active in FEM» (Активна во время расчета) – объем объекта вычисляется во время расчета и в дальнейшем корректируется из условия постоянства объема [1].
Следом импортируем геометрию инструмента. Во вкладке «Общее» задаем тип объекта «Жесткий». После чего во вкладке «Движение» задаем параметры движения инструмента (рис. 1. 9).
После чего переходим в окно «Позиционирования объектов» и выставляем инструмент относительно заготовки в начальное положение для моделирования (рис. 1. 10).
|
|
|
Затем переходим в окно «Взаимодействия объектов» и настраиваем взаимодействие между инструментом и заготовкой, также вводим деформационный и температурные коэффициенты (рис. 1. 11). Потом корректируем погрешность контакта и генерируем контакт между объектами.
Заходим во вкладку «Материал» и задаем некоторые свойства материала, а именно «Твердость», для стали 38ХМА вводим параметры прокаливаемости (табл. 1. 1) по кривой Jominy (рис. 1. 12).
После чего переходим во вкладку «Дополнительно» и вводим критерий разрушения Cockcroft & Latham (рис. 1. 13).
Последним этапом в окне препроцессора является генерация базы данных (рис. 1. 14).
После генерации базы данных выходим с препроцессора и переходим в окно DEFORM-3D (рис. 1. 15).
Сбоку во вкладке «Simulator» нажимаем кнопку «Старт» и начинается расчет моделирования, который можно просмотреть как наглядно нажав на кнопку «Simulation Graphics» так и в текстовом формате перейдя на вкладку «Сообщения».
|
|
|


