 |
Методические указания к решению задачи 2
|
|
|
|
Методические указания к решению задачи 2
Решение задачи 2 требует знания методики определения эквивалентной емкости цепи при смешанном соединении конденсаторов в цепи постоянного тока, а также умения вычислять величину заряда и энергии электрического поля каждого конденсатора и всей цепи.
ПРИМЕР 2
В цепи: С1 = 8мкФ, С2 = 4мкФ, С3 = 6мкФ, С4 = 4мкФ, U = 36В.
Определить эквивалентную емкость цепи, а также заряд и энергию электрического поля каждого конденсатора и всей цепи.
Решение:
1. Конденсаторы С1 и С2 включены параллельно, их эквивалентная емкость:
С12 = С1 + С2 = 8 + 4 = 12мкФ.
2. Конденсаторы С12 , С3, С4 соединены последовательно, их эквивалентная
емкость:
, откуда 
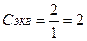мкФ.
3. Определим величину заряда в цепи: Q = Cэкв ∙ U = 2∙ 36 = 72 мкКл.
4. Определим величину напряжения на обкладках каждого конденсатора:
; 
; 
.
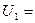
5. Определим энергию электрического поля каждого конденсатора:
; 
;
; 
.
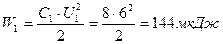6. Определим сумму энергий электрических полей всех конденсаторов:
W = W1 + W2 + W3 + W4 = 144 + 72 + 432 + 648 = 1296 мкДж.
7. Выполним проверку, определив энергию электрического поля всей цепи:
.
1296мкДж = 1296мкДж Задача решена верно.
Методические указания к решению задачи 3
Перед решением задачи 3 рассмотрите решение типового примера расчета сложной электрической цепи тремя различными методами:
ПРИМЕР 3
а) метод контурных токов:
Определить токи в отдельных ветвях цепи, если:
Е1=10 В, Е2= 40 В, R1= 8 Oм, R2= 40 Oм, R3= 10 Oм
Решение:
1. Задаемся произвольным направлением тока в обоих контурах, например, по часовой стрелке и составляем уравнения по второму закону Кирхгофа
при обходе каждого контура:
|
|
|
2. Решив эту систему двух уравнений с двумя неизвестными, найдем контурные ток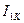и 
и 
:
Переписываем второе уравнение в системе с перемещением неизвестных:
С целью выравнивания коэффициентов при 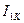домножим все члены второго уравнения на 1, 2
Суммируем оба уравнения и определяем контурный ток :
Подставляем найденное значение в первое уравнение и определяем контурный ток :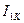
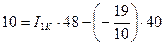
Полученные значения контурных токов со знаком (-) говорят лишь о том, что фактическое направление токов в контурах противоположно произвольно выбранному, т. е. против часовой стрелки.
3. Определяем токи в ветвях:
; 
;
Проверка:
+ 
= 
= 
= 
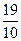Решение:
б) метод узлового напряжения:
1. Задаемся произвольным направлением тока в ветвях к одному из узлов, например, вверх, и находим напряжение между узлами:
2. Определяем направления и величины токов в ветвях:
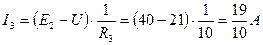
3. Знак (-) в полученных величинах говорит о том, что фактическое направление тока противоположно произвольно выбранному.
Решение:
в) метод суперпозиции (наложения):
1. На основе исходной схемы составляем частные расчетные схемы, в каждой из которых действует только одна ЭДС, определяем частные токи и алгебраическим сложением частных токов с учетом их направления находим величины токов в исходной схеме:
В частной схеме а) определяем частные токи в ветвях I1a, I2a, I3a:
;
;
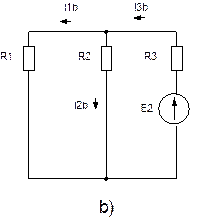
В частной схеме b) определяем частные токи в ветвях I1b, I2b, I3b:
;
;
.
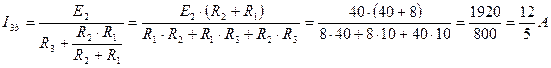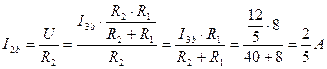Производим алгебраическое сложение полученных частных токов:
;
;
.
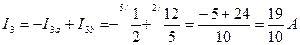Значение тока I1 получилось отрицательным, что говорит о работе источника ЭДС Е1 в режиме потребления электроэнергии.
Методические указания к решению задачи 4
Перед решением задачи 4 рассмотрите решение типового примера расчета индуктивности кольцевой катушки:
|
|
|
ПРИМЕР 4
Определить индуктивность катушки, равномерно намотанной на текстоли-товый кольцевой замкнутый сердечник с круговым поперечным сечением, с числом витков w = 500, проходящим по ней постоянным током I = 2A, и значение ЭДС, индуктируемой в обмотке, если ток прекращается за время t =1мсек. Наружный диаметр кольца D1=300 мм, внутренний D2=200 мм
Решение:
1. Определяем длину средней магнитной линии:
.
2. Определяем напряженность магнитного поля:
3. Определяем величину магнитной индукции:
B=μ oH= 
4. Определяем площадь поперечного сечения кольцевого сердечника:
S= 
5. Определяем величину магнитного потока катушки:
Ф=BS= 0, 16∙ 10-2∙ 0, 785∙ 10-2 = 0, 1256∙ 10-4 Вб.
6. Определяем потокосцепление:
Ψ =Фw= 0, 1256∙ 10-4 ∙ 500 = 0, 628∙ 10-2 Вб;
7. Определяем индуктивность катушки:
L= 
8. Определяем величину индуктированной ЭДС:
e= 
Примечание: при наличии ферромагнитного сердечника ЭДС была бы больше в μ раз ( μ стали = 102 − 104 )
|
|
|
