 |
Методические указания к решению задачи 5
|
|
|
|
Методические указания к решению задачи 5
Перед решением задачи 5 изучите материал темы «Однофазные электрические цепи переменного тока», ознакомьтесь с методикой построения векторных диаграмм, и разберите решение типового примера 5
ПРИМЕР 5.
Неразветвленная цепь переменного тока содержит активное R = 8 Ом, индуктивное XL = 4 Ом и емкостное ХC = 10 Ом сопротивления. Напряжение на зажимах цепи U= 200 В (действующее значение).
Определить:
1) полное сопротивление цепи Z;
2) угол сдвига фаз φ (по величине и знаку);
3) ток в цепи I;
4) активную Р, реактивную Q и полную S мощности, потребляемые цепью.
Начертить в масштабе векторную диаграмму цепи и пояснить ее построение.
Решение:
1. Полное сопротивление цепи
где Х – общее реактивное сопротивление цепи, равное
2. Угол сдвига фаз φ (по величине и знаку)
Во избежание потери знака угла (косинус - функция четная) определяем sin φ :
По таблицам Брадиса или с помощью микрокалькулятора определяем угол φ = - 36°52' < 0 и коэффициент мощности соs φ = cos (-36°52') = 0, 8.
Проверка: 
Sin φ < 0, так как XL < ХC, отсюда угол φ < 0.
3. Ток в цепи определяем по закону Ома:
4. Определяем активную мощность цепи:
5. Реактивная мощность цепи:
Q = UIsinφ = 200 ∙ 20 ∙ (-0, 6) = -2400 вар < 0
или Q = I2X = I2(XL – ХC) = 202 ∙ (4 – 10) = 202 ∙ (-6) = -2400 вар< 0,
так как XL < ХC Þ Q < 0.
6. Полная мощность цепи:
S = UI = 200 ∙ 20 = 4000 В∙ А,
или S = I2Z = 202 ∙ 10 = 4000 В∙ А,
или 
7. Построение векторной диаграммы:
а) определяем падения напряжения на всех участках цепи:
б) выбираем масштабы тока т1 = 5 А/см и напряжения тU = 50 В/см;
в) определяем, пользуясь выбранными масштабами тока и напряжения, длины векторов тока и падений напряжения на всех участках цепи:
|
|
|
г) при построении векторной диаграммы за начальный принимается вектор тока 
, так как ток имеет одинаковое значение для всех участков неразветвленной цепи. Далее следует строить векторы напряжений на каждом сопротивлении с учетом сдвига фаз относительно вектора тока:
вектор напряжения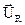 
на активном сопротивлении R строим от начала вектора тока параллельно вектору тока, так как между векторами и 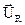сдвига фаз нет;
вектор напряжения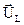 
на индуктивном сопротивлении XL строим от конца вектора 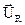под углом 90° в сторону опережения (вверх) вектора тока , а значит, и вектора 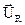, так как напряжение на индуктивности опережает на 90° по фазе ток в ней;
вектор напряжения 
на емкостном сопротивлении ХC строим от конца вектора 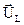под углом 90° в сторону отставания (вниз) от вектора тока , так как напряжение на емкости отстает от тока в ней на 90° по фазе.
Вектор напряжения 
на зажимах цепи находим геометрически сложением векторов 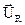, 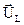и по правилу многоугольника: начало принятого за первый вектора 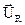соединяем с концом последнего вектора , т. е. имеем:
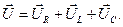
Угол между векторами тока и напряжения на входных зажимах цепи обозначают φ и называют углом сдвига фаз данной цепи.
| Проверка построения
1) транспортиром измерим величину угла φ : φ = -36°52', т. е совпадает с расчетной величиной (пункт 2);
2) измерим линейкой длину вектора :  = 4 см, тогда величина этого напряжения будет:
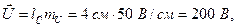что соответствует условию задачи: U = 200 В.
Значит, диаграмма построена верно.
|
Методические указания к решению задачи 6
Перед решением задачи 6 изучите материал темы «Однофазные электрические цепи переменного тока», ознакомьтесь с методикой построения векторных диаграмм, и разберите решение типового примера
ПРИМЕР 6
|
|
|
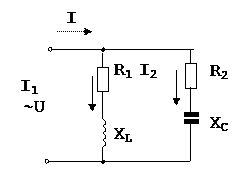
Цепь переменного тока состоит из двух ветвей, соединенных параллельно. Первая ветвь содержит катушку с активным R1=12 Ом, и индуктивным XL=16 Ом сопротивлениями, во вторую включен конденсатор с емкостным сопротивлением XC =8 Ом и последовательно с ним активное сопротивление R2 =6 Ом. Активная мощность, потребляемая первой ветвью, P1 =48 Вт. Определить: 1) токи в ветвях и в неразветвленной части цепи; 2) напряжение, приложенное к цепи; 3) активные и реактивные мощности цепи; 4) угол сдвига фаз между током в неразветвленной части цепи и напряжением. Построить в масштабе векторную диаграмму цепи.
Решение:
1. Активная мощность Р1 теряется в активном сопротивлении R1
, отсюда определяем величину тока в первой ветви:
.
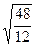
2. Определяем напряжение, приложенное к цепи:
.
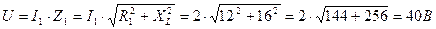3. Определяем величину тока во второй ветви:
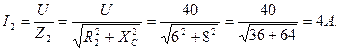
4. Находим активную и реактивную мощности, потребляемые цепью:
Знак « - » показывает, что преобладает реактивная мощность емкостного характера
Полная мощность, потребляемая цепью, составит:
.
5. Определяем величину тока в неразветвленной части цепи:
6. Угол сдвига фаз во всей цепи находим через sin φ во избежание потери
знака угла:
Знак «-» означает, что ток в цепи опережает напряжение.
7. Для построения векторной диаграммы определяем углы сдвига фаз в ветвях:
;
.
Задаемся масштабом по току: в 1см – 1А и напряжению: в 1 см – 5В.
За исходный принимаем вектор напряжения. Под углом 
к нему в сторону отставания откладываем в масштабе вектор тока I1, под углом 
в сторону опережения – вектор тока I2. Геометрическая сумма векторов этих токов равна вектору тока в неразветвленной части цепи:
Векторная диаграмма цепи примера № 6
|
|
|
