 |
Вероятность случайного события
|
|
|
|
Событие – появление определенного признака. Вероятность признака – относительное число появлений признака.
Пример. Для газа в сосуде концентрация частиц около точки r
изменяется с течением времени хаотически.
Событие – наблюдение определенной концентрации 
.
Если измерение проводится N раз и результат наблюдается 
раз, то вероятность результата
, (1.1)
.
Зависимость 
называется функцией распределения вероятностей событий с определенным признаком.
Теорема 1. Сложение вероятностей несовместимых событий А 1, А 2,…, Аk, которые не могут произойти одновременно. Например, при бросании кости можно получить результат: или 1, или 2,… Вероятность сложного события с положительным исходом A или B
. (1.2)
Если (А 1, А 2,…, Аk) – полный набор возможных событий, то число измерений
.
Вероятность полного набора событий согласно (1.2) и (1.1)
,
где сделана замена порядка операций суммирования и взятия предела.
Нормировка вероятностей для полного набора событий
. (1.3)
Пример. Движения молекулы газа вдоль и против некоторой оси образуют полный набор независимых направлений движения
W (влево) + W (вправо) = 1.
Если гамильтониан изотропен, то все направления равноправные и
W (влево) = W (вправо) = 1/2.
Теорема 2. Умножение вероятностей независимых событий А 1, А 2,…, Аk, которые не влияют друг на друга. Вероятность сложного события А 1, и А 2,…, и Аk
. (1.4)
Пример. В объеме V 0, все точки которого равноправны, находится одна частица. Объем V 0 разбиваем на N одинаковых ячеек объемом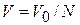 
. При обследовании всех ячеек, т.е. при 
измерениях, положительный результат будет только в одной ячейке. Вероятность найти частицу в одной произвольной ячейке согласно (1.1)
|
|
|
. (1.4а)
Если в V 0 находится m независимых частиц, то вероятность, что весь газ окажется в объеме V, согласно (1.4) равен
. (1.4б)
Характеристики случайной дискретной величины
Среднее значение величины
Пусть для x возможны значения: x 1, x 2, …, xk.
Измерения проводятся N раз, результат xi наблюдается Ni раз, тогда
.
Среднее значение
.
При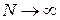 
согласно (1.1) получаем
,
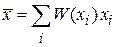. (1.5)
Среднее значение величины равно сумме произведений ее значений на вероятности этих значений.
При 
получаем 
и (1.5) дает нормировку вероятностей
. (1.6)
Свойства среднего
Для 
и независимых случайных величин x и y выполняются
1. 
,
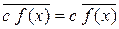2. 
,
3. 
.
Доказательство 2. Используя (1.5), получаем
;
Доказательство 3.
,
где для независимых случайных величин учтена теорема 2
.
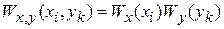Отклонение от среднего
.
Среднее отклонение от среднего
.
Среднее квадратичное величины
. (1.7)
Среднее квадратичное отклонения от среднего – дисперсия
. (1.8)
Флуктуация
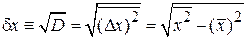. (1.9)
Относительная флуктуация
. (1.10)
Если x случайным образом изменяется с течением времени, то относительная флуктуация показывает долю времени, в течение которой система находится в состоянии с 
.
Теорема: Относительная флуктуация аддитивной величины, характеризующей систему, уменьшается обратно пропорционально корню квадратному из числа независимых подсистем и мала для макроскопической системы. Примером аддитивной величины (от лат. additivus – прибавляемый) является энергия. Флуктуация энергии для макросистемы ничтожно мала, для микросистемы она существенна.
Доказательство
Аддитивная величина X для системы равна сумме значений xk для N независимых подсистем
|
|
|
, 
.
Тогда
,
,
,
где
,
и усреднение произведений характеристик статистически независимых подсистем
, 
.
Относительная флуктуация
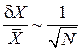. (П.1.2)
ХАРАКТЕРИСТИКИ СЛУЧАЙНой
НЕПРЕРЫВНой ВЕЛИЧИНы
Плотность вероятности случайной величины x равна вероятности ее обнаружения в единичном интервале около значения x
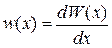. (1.11)
Вероятность нахождения в интервале 
.
Пример: Пусть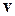 
– скорость частицы идеального газа. Вероятность обнаружения частицы со скоростью в интервале 
,
– концентрация частиц со скоростями в интервале ,
n – концентрация частиц со всевозможными скоростями.
Условие нормировки
. (1.12)
Средние значения
,
. (1.13)
|
|
|
