 |
Биномиальное распределение.
|
|
|
|
Описывает N независимых частиц или N независимых случаев.
Если p – вероятностьпризнака у одной частицы, или вероятность одного случая, то вероятностьтого, что n любых частиц обладают этим признаком, или вероятность одновременного возникновения n случаев:
, (1.14)
; 
;
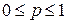– биномиальный коэффициент.
Распределение обосновал Якоб Бернулли в 1713 г.
Доказательство:
Объект – идеальный газ из N тождественных частиц в объеме V.
Получим вероятность обнаружения n любых частиц в объеме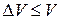 
.
1. Вероятность найти определенную частицу в объеме D V согласно определению вероятности (1.4а)
.
Вероятность найти определенную частицу вне объема D V
.
Несовместимые события образуют полный набор и удовлетворяют условию нормировки.
2. Вероятность найти n определенных частиц в объеме D V согласно теореме об умножении вероятностей независимых событий (1.4б)
.
Вероятность найти (N – n) определенных частиц вне объема D V
.
3. Вероятность найти одновременно n определенных частиц в объеме D V и (N – n) других частиц вне этого объема
.
4. Взаимная перестановка тождественных частиц дает состояние, не отличимое от исходного. Число таких состояний равно числу сочетаний n частиц из общего числа N, т. е. равно 
.
5. В результате вероятность найти n любых частиц в объеме D V и (N – n) любых других частиц вне D V
.
Условие нормировки
,
использован бином Ньютона
.
Среднее число частиц в объеме D V
.
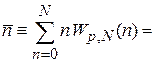
Замена 
и бином Ньютона дают
= 
= 
.
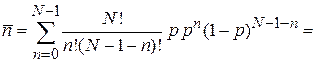
Результат
(1.15)
очевиден, поскольку 
– средняя концентрация.
Из (1.15) вероятность признака у одного элемента
|
|
|
. (1.16)
Из (1.14) получаем – если в некотором состоянии наблюдается в среднем 
частиц, то вероятность наблюдения n частицравна
, (1.17)
причем
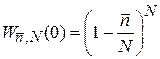, (1.17а)
. (1.17б)
График распределения
а б
Распределения биномиальное (а) и Пуассона (б) для N = 10, 
, р = 0,45
Распределение Пуассона
При малой вероятности наблюдения в некотором состоянии одной частицы 
и при большом числе частиц 
вероятность найти n частиц, если в среднем их , равна
. (1.18)
Распределение следует из биномиального распределения, его получил Симеон Дени Пуассон в 1837 г.
Доказательство:
Записываем биномиальное распределение (1.17)
,
учтено
.
При 
используем
,
,
,
и получаем (1.18).
Условие нормировки
,
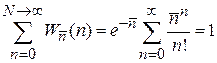где
.
Частные и рекуррентные соотношения
,
,
,
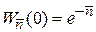. (1.18а)
График распределения
а б
Распределения биномиальное (а) и Пуассона (б) для N = 10, , р = 0,45
При 
вероятность монотонно уменьшается с увеличением n.
Нормальное распределение Гаусса
При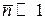 
и относительно малом отклонении от среднего 
выполняется нормальное распределение
. (1.19)
Распределение получил Карл Фридрих Гаусс в 1809 г.
Доказательство:
Распределение Пуассона
логарифмируем
.
Используем формулу Стирлинга
,
,
тогда
.
Используя
, 
,
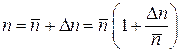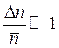разлагаем в ряд
.
В результате
.
Заменяя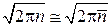 
и потенцируя, получаем (1.19).
Условие нормировки
На основании 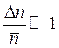считаем n квазинепрерывным, тогда
,
Условие нормировки получает вид
,
где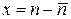 
; 
, поскольку , 
;
.
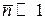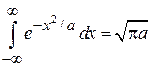Среднее значение
,
,
,
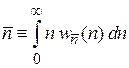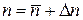где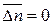 
.
Дисперсия
,
где учтено
.
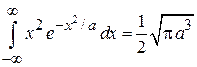В результате
. (1.20)
Из (1.19) и (1.20) плотность вероятности
. (1.21)
Распределение Гаусса, 
Распределение Гаусса в пределе бесконечно малой дисперсии является дельта-функцией
|
|
|
. (1.21а)
Это следует из (1.21) и
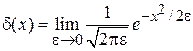
Центральная предельная теорема – при суммировании большого числа независимых случайных величин, имеющих различные распределения, результирующее распределение близко к распределению Гаусса.
Теорему доказал Александр Михайлович Ляпунов в 1901 г.
Теорема обосновывает применимость нормального распределения к многочисленным случайным процессам.
ПРОИЗВОДЯЩАЯ ФУНКЦИЯ
Для дискретного распределения 
случайной величины n () производящая функция
, (1.22)
где | x | £ 1. Функция распределения
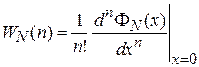. (1.23)
Средние значения и дисперсия
,
,
.
Из (1.22) находим
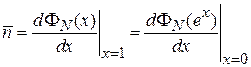, (1.24)
,
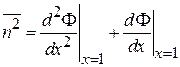, (1.25)
. (1.26)
ПРИМЕРЫ
1. Для распределения Пуассона найти производящую функцию и 
.
Используем производящую функцию (П.1.5) для биномиального распределения и (П.1.6)
, 
,
тогда
.
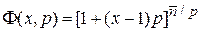Учитывая 
и
,
где 
, получаем производящую функцию распределения Пуассона
. (П.1.14)
Из (П.1.14) и (1.25)
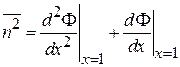
с учетом
, 
,
следует (1.20)
.
2. Найти распределение времен свободного пробега электрона металла.
Согласно классической теории в узлах кристаллической решетки металла находятся ионы, валентные электроны образуют идеальный газ. Любой макроскопический объем металла электрически нейтрален, поэтому на электрон не действуют электростатические силы и благодаря тепловому движению он свободно перемещается от одного столкновения с ионом до следующего.
Вероятность столкновения электрона за единицу времени а не зависит от t при термодинамическом равновесии. Вероятность столкновения за время dt равна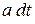 
.
Функция распределения времен свободного пробега w (t) равна вероятности того, что время свободного движения лежит в единичном интервале около значения t.
Вероятность двух независимых событий – свободного движения электрона до момента t и столкновения в следующий промежуток dt – согласно теореме о независимых событиях равна 
и является уменьшением вероятности обнаружения электрона при переходе от t к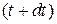 
, т. е. равна 
. В результате
.
Разделяя переменные и интегрируя, получаем,
, 
.
Из условия нормировки
|
|
|
находим 
. Среднее время свободного пробега
(П.1.22)
обратно вероятности столкновения за единицу времени. Функция распределения времен свободного пробега равна
(П.1.23)
– вероятность свободного движения в течение времени t уменьшается экспоненциально с ростом t.
3. Найти скорость дрейфа 
электронов металла в электрическом поле Е.
За время свободного пробега t электрон набирает скорость 
, где ускорение 
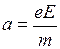. Если при столкновении упорядоченная скорость теряется, то средняя скорость
.
Время свободного пробега меняется от столкновения к столкновению. Пусть электрон испытывает последовательно N столкновений с временами свободного пробега t 1, t 2,…, tN и средними скоростями 
, тогда скорость дрейфа
.
Поделив числитель и знаменатель на N, и полагая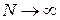 
, получаем
.
Используя распределение (П.1.23), находим
,
.
В результате скорость дрейфа
(П.1.24)
пропорциональна электрическому полю и среднему времени t свободного пробега электрона, где подвижность электронов
.
|
|
|
