Тема 3. Пропозициональная логика

 

или логика элементарных высказываний изучает свойства логических операций Ø, Ù, Ú, Þ, Û, которые по смыслу их введения являются операциями над истинностными значениями:

 

p	q	Ø p	p Ù q	p Ú q	p Þ q	p Û q
Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	И	Л
И	Л	Л	Л	И	Л	Л
И	И	Л	И	И	И	И

 

Если высказывания р, q различны и элементарны, то эта таблица называется истинностной таблицей высказываний (p, q,) Øp, pÙq, pÚq, pÞq, pÛq. В общем случае при составлении истинностной таблицы какого-либо перечня высказываний надо поместить на ее вход все различные пропозициональные компоненты этих высказываний, сделать полный перебор истинностных значений во входных столбцах и записать соответствующие истинностные значения в результирующих столбцах.

 

Пример. В комнате без окон темно и неуютно.

Универсум - множество комнат

g (c₁) - c₁ имеет окно                p - комната имеет окно

g (c₁) - в c₁ темно                       q - в комнате темно

g (c₁) – в c₁ уютно                    r - в комнате уютно

 

(Ø(g (c₁)))Þ((g (c₁))Ù(Ø(g (c₁))))     ØpÞqÙØr

   p            q            r

 

p	q	r	Ø p	Ø r	q Ù Ø r	Ø p Þ q Ù Ø r
Л	Л	Л	И	И	Л	Л
Л	Л	И	И	Л	Л	Л
Л	И	Л	И	И	И	И
Л	И	И	И	Л	Л	Л
И	Л	Л	Л	И	Л	И
И	Л	И	Л	Л	Л	И
И	И	Л	Л	И	И	И
И	И	И	Л	Л	Л	И

 

Тавтология или тавтологически истинное высказывание - это высказывание со сплошными И в его столбце его истинностной таблицы. Высказывание q называется тавтологическим следствием (из) высказываний p₁,…,p_n, если в истинностной таблице высказываний p₁,…,p_n,,q столбец q содержит И в любой строке, которая содержит И во всех столбцах p₁,…,p_n. Например, построенная выше таблица показывает, что:

ØpÞqÙØr - есть тавтологическое следствие из Øp, qÙØr;

Ør, q являются тавтологическими следствиями из qÙØr;

 r есть тавтологическое следствие из p, Øp.

        

Теорема об отрицании отрицания: ØØp = p

Теорема об отрицании конъюнкции: Ø(pÙq) = ØpÚØq

Теорема об отрицании дизъюнкции: Ø(pÚq) = ØpÙØq

Теорема об исключении импликации: pÞq = ØpÚq

Теорема об исключении эквиваленции: pÛq = pÙqÚØpÙØq

Теорема об устранении альтернативы: pÚØpÙq = pÚq, ØpÚpÙq = ØpÚq

Теорема о коммутативности конъюнкции: pÙq = qÙp

Теорема о коммутативности дизъюнкции: pÚq = qÚp

Теорема об ассоциативности конъюнкции: pÙ(qÙr) = (pÙq)Ùr

Теорема об ассоциативности дизъюнкции: pÚ(qÚr) = (pÚq)Úr

Теорема о дистрибутивности конъюнкции: pÙ(qÚr) = (pÙq)Ú(pÙr)

Теорема о дистрибутивности дизъюнкции: pÚ(qÙr) = (pÚq)Ù(pÚr)

Теорема о равносильности: р = q тогда и только тогда когда pÛq = И

Теорема  о тавтологическом следствии: q является тавтологическим

следствием из р₁,…,p_n  тттк р₁Ù…Ùр Þ q является тавтологией. Эти три теоремы

легко доказываются с помощью истинностных таблиц.

 

Арифметический способ записи высказываний: исключаются знаки Þ, Û

и вместо Л, И, Øp, pÙq, pÚq употребляются соответственно 0, 1, `p, p q, p + q.

Например, арифметической записью высказывания (rÚpÞqÙr) будет .

При арифметической записи высказываний с ними можно обращаться так, как будто они обозначают числа 0, 1, а. Логический плюс отличается от арифметического только тем, что 1 + 1 = 1. При этом полезно помнить следующие равенства:

p Þ q = `p + q                                         

p Û q = p q + `p `q                                  p p = p

                                             p + p = p

                                                 p`p = 0

p + `p q = p + q                                    p +`p = 1

p + p q = `p + q                                        1 + p = 1

Равенства в левой колонке представляют собой другую запись уже доказанных выше теорем, а равенства в правой колонке устанавливаются непосредственной проверкой с учетом равенств 0 = 1, 1 = 0.

Пример. Доказательство тавтологичности высказываний:

 

pÞqÞp =`p + (qÞp) =`p +`q + p =`p + p +`q = 1 +`q = 1

pÞqÞpÙq =`p +`q + p q =  + p q = 1

(ØpÞØq)Þ(ØqÞp)Þq =   +q =`q p +`q`p + q = `q (p +`p) + q =`q + q = 1

 

Пример. Выразительная достаточность пар ØÙ, ØÚ, ØÞ.

 

pÙq = Ø(ØpÚØq) = Ø(pÞØq)

pÚq = Ø(ØpÙØq) = ØpÞq

pÞq = Ø(pÙØq) = ØpÚq

pÛq = Ø(Ø(pÙq)ÙØ(ØpÙØq))

pÛq = Ø(ØpÙq)ÙØ(pÙq)

pÛq = Ø((pÞq)Þ Ø(qÞp))

 

Доказательство последнего равенства:

pÛq = p q +`p`q

Ø((pÞq)ÞØ(qÞp)) =  = (`p + q)(q +`p) = `p`q +`p p +`q q + q p =`p`q + 0 + 0 + q p = p q +`p`q

 

Пример. Упрощение высказываний.

        

(ØpÚØqÚØr)Ù(qÚØp)Ú(pÞq)Ùq = (`p +`q +`r)(q +`p) + q(`p + q) = (`p + q)(`p +`q +`r + q) = (`p + q)(1 +`p + `r) = `p + q = pÞq

(pÞq)Þp =  + p = p`q + p = p(`q + 1) = p 1 = p

 

Пример. Доказательство равносильности высказываний.

[ØpÞØqÙØr] = `p Þ`q`r = `p +`q`r = p +`q`r

{(ØpÞØq)Ù(ØpÞØr)} = (`pÞ`q)(`pÞ`r) = (p +`q)(p +`r) = p + p`r +`q p +`q`r = p(1 +`r +`q) +`q`r = p +`q`r

Т. о. […] = {…} т. е. являются равносильными два полученных ранее перевода высказывания «чай …».

 

Правилом отделения называется правило D p, (p)Þ(q), q

Теорема о выводе в пропозициональной логике: высказывание p₀ является тавтологическим следствием из p₁,…,p_n тттк его можно получить из p₁,…, p_n с помощью правила отделения и нижеследующих пятнадцати беспосылочных правил:

D pÞqÞp

D (pÞpÞq)Þ(pÞq)

D (pÞq)Þ((qÞr)Þ(pÞr))

D pÙqÞp

D pÙqÞq

D (pÞq)Þ((pÞr)Þ(pÞqÙr))

D pÞpÚq

D qÞpÚq

D (pÞr)Þ((qÞr)Þ(pÚqÞr))

D (pÛq)Þ(pÞq)

D (pÛq)Þ(qÞp)

D (pÞq)Þ((qÞp)Þ(pÛq))

D (pÞq)Þ(ØqÞØp)

D pÞØØp

D ØØpÞp

 

Другими словами, какое–либо высказывание p₀ является тавтологическим следствием из p₁,…,p_n  тттк p₀ можно сделать членом последовательности высказываний, которая является индуктивной относительно этих шестнадцати правил и правил D p₁,…, Dp_n. Теорема не исключает случай n = 0.

Теорема о самодостаточной выразительности пропозициональной логики: для любой истинностной таблицы с n входными столбцами p₁,…,p_n и любого распределения истинностных значений в ее результирующем столбце можно составить соответствующее этому столбцу высказывание: справа от всех строк с истиной в результирующем столбце записываем конъюнкцию p₁… p_n, затем над некоторыми p_k ставим черту отрицания так, чтобы все эти конъюнкции для всех строк были истинными, затем составляем дизъюнкцию из получившихся конъюнкций. Например:

p            q            r           ?

0            0            0            0

0            0            1            0

0            1            0            1            p q`r

0            1            1            0

1            0            0            1            p`q`r

1            0            1            0

1            1            0            1            p q`r

1            1            1            0

 

`p q`r + p`q`r + p q`r = `p q`r + p`r(`q + q) =`p q`r + p`r =`r(`p q + p) =`r(p + q) = ØrÙ(pÚq)

Замечание. Если в результирующем столбце содержится только Л, то в качестве искомого высказывания можно взять p₁ÙØp₁.

Пример применения теоремы о самодостаточной выразительности. Турист приехал в страну, где каждый житель всегда лжет либо всегда говорит правду. Какой вопрос должен задать турист местному жителю, чтобы узнать, какая из двух дорог ведет в столицу.

p – житель говорит правду

q – эта дорога ведет в столицу

r – высказывание для вопроса

p	q	r	Нужный ответ
0	0	1	Нет	`p`q
0	1	0	Да
1	0	0	Нет
1	1	1	Да	p q

 

r =`p`q + p q = pÛq т. e. турист должен спросить: верно ли, что Вы скажите правду если и только если эта дорога ведет в столицу.

 

Пример проверки рассуждения «(Профсоюзы поддержат президента на предстоящих выборах | p) только если (он подпишет законопроект о повышении заработной платы ½q). (Фермеры окажут президенту поддержку ½r) только если (он наложит вето на законопроект ½s). Очевидно, что он не подпишет законопроекта или не наложит на него вето. Следовательно президент потеряет голоса профсоюзников или голоса фермеров».

(pÞq)Ù(rÞs)Ù(ØpÚØs) Þ ØpÚØr =  +`p +`r =`p q + r s + q s +`p +`r =  + q s =  + q s =`p +`q +`r +`s +q s =`p +`r +  + q s = `p +`r +1 = 1 – тавтология, т.е. рассуждение правильное.

 

    Пример проверки рассуждения «(В бюджете возникнет дефицит | p), если (не повысят пошлины | Øq). Если в бюджете будет дефицит, то (государственные расходы на общественные нужды сократятся | r). Значит, если повысят пошлины, то государственные расходы на общественные нужды не сократятся».

(ØqÞp)Ù(pÞr)Þ(qÞØr) =  +`q + `r =`q`p + p`r +`q +`r = `q(`p +1) +`r(p + 1) =`q +`r =  - не тавтология, т.е. нельзя сказать, что рассуждение правильно.

 

Пример проверки рассуждения «Если (подозреваемый совершил эту кражу | p), то (она была тщательно подготовлена | q) или (он имел соучастника | r). Если бы кража была подготовлена тщательно, то, если бы был соучастник, украдено было бы гораздо больше. Значит, подозреваемый невиновен».

(pÞqÚr)Ù(qÞ(rÞØp))ÞØp =  +`p = p`q`r + p q r +`p = q r +`q`r +`p

– не тавтология.

 

Пример проверки рассуждения «(Если наступит мир | p), то (возникнет депрессия | q), разве что (страна проведет программу перевооружения | r) или осуществит грандиозную социальную программу | s). Но договориться о целях такой грандиозной программы невозможно. Следовательно если наступит мир и не будет депрессии, то будет осуществляться программа перевооружения».

(pÞqÚØqÙ(rÚs))ÙØsÞpÙØqÞr =  =

т.е. рассуждение правильное.

 

Пример сокращения текста «Члены финансового комитета должны избираться среди членов дирекции. Нельзя быть одновременно членом дирекции и членом библиотечного совета, не будучи членом финансового комитета. Член библиотечного совета не может быть членом финансового комитета».

 

p – он является членом финансового комитета

q – он является членом дирекции

r – он является членом библиотечного фонда

(pÞq)Ù(ØpÞØ(qÙr))Ù(rÞØp) = (`p + q)(p +`q +`r)(`r +`p) = (`p +q)  = (`p + q) 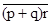=(`p + q)(`p`q +`r) = (`p + q)(`p + q)`q +`r) = (`p + q)(`q +`r) = (pÞq)ÙØ(qÙr)

Таким образом, можно отбросить подчеркнутую часть текста.

Пример анализа рассуждения «(это преступление совершено в Кустанае | q). (Петров во время совершения преступления находился в Ростове | r). Следовательно (Петров не совершал этого преступления | Øp)».

qÙrÞØp – не тавтология

«Преступление совершено в Кустанае. Поэтому если Петров совершил это преступление, то (он во время совершения преступления находился в Кустанае |s). Но Петрова в это время в Кустанае не было. Значит, Петров не совершал этого преступления».

qÙ(qÞpÞs)ÙØp = … = 1 – тавтология т.е. рассуждение правильное.

Рассуждение останется правильным, если из него выбросить первое предложение и ссылку на него во втором предложении:

(pÞs)ÙØsÞØp =  +`p =  +`p = p + s +`p = 1 + s = 1

Задача. Выяснить, кто из четверых виновен на основе информации «Петров виновен, только если виновен Кулагин. Неверно, что виновность Родионова влечет виновность Сидорова и что Кулагин виновен, а Сидоров нет».

p, q, r, s – виновен Петров, Кулагин, Родионов, Сидоров.

(pÞq)ÙØ(rÞs)ÙØ(qÙØs) = (`p + q)  = (`p + q) r`s(`q + s) = (`p + q)`r s`q = `p`q r`s

т.е. Родионов виновен, остальные не виновны.

Задача Кислера. Обвиняемые в подделке налоговых документов Браун, Джонс и Смит дают под присягой такие показания.

Браун: Джонс виновен, а Смит не виновен.

Джонс: Если Браун виновен, то виновен и Смит.

Смит: Я не виновен, но хотя бы один из них двоих виновен.

 

Вопрос 1: Совместимы ли данные показания?

Вопрос 2: Какое показание следует из другого?

Вопрос 3: Если все виновны, то кто лжесвидетельствует?

Вопрос 4: Если все сказали правду, то кто виновен?

Вопрос 5: Если невинный говорит правду, а виновный лжет, то кто виновен, а кто невиновен?

 

Б – виновен Браун.

Д – виновен Джонс.

С – виновен Смит.

 

Б	Д	С	Ø Б	Ø Д	Ø С	Б Ú Д	Д Ù Ø С	Б Þ С	Ø С Ù (Б Ú Д)
Л	Л	Л	И	И	И	Л	Л	И	Л
Л	Л	И	И	И	Л	Л	Л	И	Л
Л	И	Л	И	Л	И	И	И	И	И
Л	И	И	И	Л	Л	И	Л	И	Л
И	Л	Л	Л	И	И	И	Л	Л	И
И	Л	И	Л	И	Л	И	Л	И	Л
И	И	Л	Л	Л	И	И	И	Л	И
И	И	И	Л	Л	Л	И	Л	И	Л
Показания							Брауна	Джонса	Смита

 

1. Да, только за счет третьей строки.

2. Из первого третье.

3. Браун и Смит.

4. Джонс виновен, остальные невиновны.

5. Джонс невиновен, остальные виновны.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: