 |
Тема 7. Множества и функции.
|
|
|
|
В этой теме A, B, C, D, E, F, G, X, Y, Z, X1, Z1,…, Xn, Yn, Zn обозначают попарно различные переменные. Множество – это совокупность различных объектов, мыслимая как единый новый объект. Различные объекты, из которых составлено множество, называются его элементами. Соотношение xÎA означает, что объект х есть элемент множества A. Отрицание соотношения xÎA записывается в виде xÏA. Соотношение АÌВ означает, что А есть подмножество множества В, т.е. что каждый элемент множества А является элементом множества В. Отрицание соотношения АÌВ записывается в виде АËВ. Множество, элементами которого являются все те и только те объекты вида а, для которых истинно соотношение p, обозначается через {a|p}. Множество {x|"A(xÏA)} называется пустым множеством и обозначается символом Ø. Множество {x|x = x1Ú…Úx = xn} обозначается через {x1,…,xn}. Множество {x|xÎAÚxÎB} называется объединением множеств А, В и обозначается через АÈВ. Множество {x|xÎAÙxÎB} называется пересечением множеств А, В и обозначается через АÇВ. Множество {x|xÎAÙxÏB} называется дополнением множества В относительно А или результатом удаления из множества А элементов множества В и обозначается через А\В.
Простейшие теоремы: 3Ï{9, 7, 3}, {x+5|x2 = 4} = {3, 7], AÏA, AÌA, …
Обозначения для некоторых множеств:
N - множество натуральных чисел
Z - множество целых чисел
R - множество действительных чисел
Упорядоченная n-ка объектов x1,…,xn обозначается через (x1,…,xn) и определяется так: (x1) = x1
(x1, x2) = {{x1}, { x1, x2}}
(x1, x2, x3) = ((x1, x2), x3)
(x1, x2, x3,x4) = ((x1, x2, x3), x4)
………………………………..
Упорядоченная n-ка называется еще n-мерным упорядоченным набором, вектором, точкой, кортежем. Объект x1 называется k-той компонентой или координатой n-мерного набора (x1,…,xn) и обозначается через koor  (x1,…,xn). Множество {x1,…,xn| x1Îz1Ù…Ù xnÎzn} называется декартовым произведением множеств z1,…,zn и обозначается через z1´…´zn. Если А - множество упорядоченных n-ок, то множество {xk|(x1,…,xnÎA} называется k-той проекцией n-мерного множества А и обозначается через π
(x1,…,xn). Множество {x1,…,xn| x1Îz1Ù…Ù xnÎzn} называется декартовым произведением множеств z1,…,zn и обозначается через z1´…´zn. Если А - множество упорядоченных n-ок, то множество {xk|(x1,…,xnÎA} называется k-той проекцией n-мерного множества А и обозначается через π  А. Через Аn обозначается множество А´…´А (n множителей). Соглашение: знаки ´, Ç, связывают сильнее чем È, \.
А. Через Аn обозначается множество А´…´А (n множителей). Соглашение: знаки ´, Ç, связывают сильнее чем È, \.
|
|
|
Простейшие теоремы: (x1,…,xn) = (y1,…,yn)Û x1= y1Ù…Ù xn= yn, (9, 9, 9)¹ (9, 9), p  (A´B´C´D´E) = C, {5. 7}2 = {(5, 5), (5, 7), (7, 5), (7, 7)}, koor
(A´B´C´D´E) = C, {5. 7}2 = {(5, 5), (5, 7), (7, 5), (7, 7)}, koor 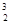 (5, 7, 9) = 9, koor
(5, 7, 9) = 9, koor  (5, 7, 9) = koor
(5, 7, 9) = koor  (5, 7, 9) = koor
(5, 7, 9) = koor  (5, 7, 9) = H, {7}´{8, 5}´{9} = {(7, 8, 9), (7, 5,9)}. {4}5 = {(4, 4, 4, 4, 4)}, p
(5, 7, 9) = H, {7}´{8, 5}´{9} = {(7, 8, 9), (7, 5,9)}. {4}5 = {(4, 4, 4, 4, 4)}, p  {(1, 2, 3), (1, 3, 2), (2, 3, 4)} = {2, 3}. A´B´C = (A´B)´C.
{(1, 2, 3), (1, 3, 2), (2, 3, 4)} = {2, 3}. A´B´C = (A´B)´C.
Функцией называется множество, любой элемент которого есть упорядоченная двойка. Множество π 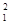 F называется областью определения или доменом функции F и обозначается dom F. Множество π
F называется областью определения или доменом функции F и обозначается dom F. Множество π  F называется областью значений или ранжиром функции F и обозначается ran F. Если (x,y)ÎF, то y называется значением функции F в x и обозначается F(x). Если АÌ domF, то множество {y|$ÎAÙ(x, y)ÎF)} называется образом множества А относительно функции F и обозначается F[А]. Функция F в случае dom F = A и ran FÌB / ranF=B называется еще отображением множества А в/на множество В. Запись F:А®В означает что F есть отображение множества А в множество В. Функция F называется сужением функции G (на множество dom F), а функция G называется расширением функции F (на множество dom G), если F есть результат удаления из G всех тех (x, y), для которых xÏ dom F. Если F есть функция, то {(y, x)ï (x, y)ÎF} тоже есть функция, называемая обратной по отношению к F. Очевидно, что если функция G является обратной по отношению к функции F, то F является обратной по отношению к G. Если dom F есть множество упорядоченных n-ок, то функция F называется n-аргументной и вместо F((x1,…,xn)) используют более короткое обозначение F(x1,…,xn). Функция F называется однозначной, если из (x, y)ÎF и (x, z)ÎF следует y=z. Функция называется взаимно однозначной или биективной, если она сама и обратная к ней функция являются однозначными. Последовательностью называется однозначная функция F т.ч. dom F = N. Если F есть последовательность и nÎ N, то F(n) называется n-м членом последовательности и обычно обозначается через Fn.
F называется областью значений или ранжиром функции F и обозначается ran F. Если (x,y)ÎF, то y называется значением функции F в x и обозначается F(x). Если АÌ domF, то множество {y|$ÎAÙ(x, y)ÎF)} называется образом множества А относительно функции F и обозначается F[А]. Функция F в случае dom F = A и ran FÌB / ranF=B называется еще отображением множества А в/на множество В. Запись F:А®В означает что F есть отображение множества А в множество В. Функция F называется сужением функции G (на множество dom F), а функция G называется расширением функции F (на множество dom G), если F есть результат удаления из G всех тех (x, y), для которых xÏ dom F. Если F есть функция, то {(y, x)ï (x, y)ÎF} тоже есть функция, называемая обратной по отношению к F. Очевидно, что если функция G является обратной по отношению к функции F, то F является обратной по отношению к G. Если dom F есть множество упорядоченных n-ок, то функция F называется n-аргументной и вместо F((x1,…,xn)) используют более короткое обозначение F(x1,…,xn). Функция F называется однозначной, если из (x, y)ÎF и (x, z)ÎF следует y=z. Функция называется взаимно однозначной или биективной, если она сама и обратная к ней функция являются однозначными. Последовательностью называется однозначная функция F т.ч. dom F = N. Если F есть последовательность и nÎ N, то F(n) называется n-м членом последовательности и обычно обозначается через Fn.
|
|
|
Множество А называется бесконечным, если существует биективное отображение множества N в множество А. Множество называется конечным, если оно не является бесконечным.
Простейшие теоремы: cos(0)=1, cos[{0}] = {1}, Аrccos и cos обратны друг к другу, функция arccos не является обратной к cos и является обратной к сужению функции cos на множество ran arccos.
ЗАДАЧНИК-МИНИМУМ ПО ЛОГИКЕ
В квадратных скобках дается ответ к задаче, Д означает ДА, Н означает НЕТ, все высказывания о числах в задачах 1.1 – 6.4 являются арифметическими, т.е. высказываниями о целых неотрицательных числах.
1.1 Указать истинное значение для высказываний 5=5, 5¹5, 5>5, 5£5, 5³5, 5<5, Х<0, Х+2<5, Х+Х<6, Х-Х=0, Х³0, X+Z=Z+X [ИЛЛИИЛЛППИИИ] и для каждых двух соседних высказываний выяснить, являются ли они равносильными [НДНДНДНДНДД].
1.2 Для каждой из трех последовательностей 2, 3; 3, 2, 4, 5; 3, 2, 3, 6 выяснить, является ли она индуктивной относительно набора правил D3; DХ, Х-1; DХ,Z,X+[НДД].
1.3 Выяснить, являются ли Dа<b, a<b+3; Da³b, b³0, a³0 правилами вывода [ДД].
2.1 Для каждого из пяти знакосочетаний ØÚ; ¦  g
g  $; f
$; f 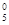 f
f 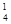 f
f  ; c4c8 f
; c4c8 f 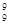 g
g 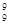 ; "$ØÙÚÞÛ выяснить следуют ли в нем его знаки в алфавитном порядке [ДНДНД].
; "$ØÙÚÞÛ выяснить следуют ли в нем его знаки в алфавитном порядке [ДНДНД].
2.2 Для терма f  (f
(f  (c1), f
(c1), f  , f
, f 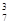 (f
(f  , c1, f
, c1, f  (f
(f  ))) составить индуктивную последовательность термов [f
))) составить индуктивную последовательность термов [f 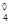 , c1, f
, c1, f  (f
(f 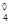 ), f
), f  (f
(f  , c1, f
, c1, f 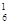 (f
(f  ) f
) f  (f
(f  (c1), f
(c1), f  , f
, f  (f
(f  , c1, f
, c1, f  (f
(f  )))].
)))].
2.3 Пусть p, q, r обозначают нульместные предикаты. Для высказывания pÚØqÙrÞpÞqÞr составить индуктивную последовательность высказываний [p, q, r, Ø(q), (Ø(q)Ù(r), (p)Ú((Ø(q))Ù(r)), (q)Þ(r), (p)Þ((q)Þ(r)), ((p)Ú((Ø(q))Ù(r)))Þ((p)Þ((q)Þ(r)))].
2.4 Для высказывания $c5g 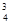 (c1, f
(c1, f  (c2), c1) составить индуктивную последовательность термов и высказываний [c1, c2, f
(c2), c1) составить индуктивную последовательность термов и высказываний [c1, c2, f  (c2), g
(c2), g 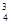 (c1, f
(c1, f  (c2), c1), $c5 (g
(c2), c1), $c5 (g 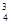 (c1, f
(c1, f  (c2), c1))].
(c2), c1))].
2.5 Для каждого из семи обозначений а: f  (a), g
(a), g  (a), g
(a), g 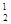 (a, b); Z; $Xg
(a, b); Z; $Xg  (X, X, Z); "Xf
(X, X, Z); "Xf 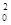 (X, X) выяснить, обозначает ли оно: Терм, Высказывание, Ни-то-ни-другое [TTBHTBH].
(X, X) выяснить, обозначает ли оно: Терм, Высказывание, Ни-то-ни-другое [TTBHTBH].
|
|
|
2.6 Для каждой из шести скобочных диад в высказывании ((p)Þ(q))Þ((r)Þ(s)) выяснить можно ли ее отбросить без нарушения смысла данного высказывания [HДДДДД].
2.7 В высказывании pÛqÚØrÙØp восстановить все скобки [(p)Û((q)Ú((Ø(r))Ù(Ø(p))))].
2.8 В высказываниях pÚØqÙrÞpÙrÚØp, pÚØqÙ(rÞpÙr)ÚØp восстановить все скобки с помощью нумерации логических знаков и скобок в порядке их восстановления.
é((p)Ú((ù(q))Ù(r)))Þ(((p)Ù(r))Ú(ù(p))), (p)Ú(((ù(q))Ù((r)Þ((p)Ù(r)))Ú(ù(p)))ù
ë76p666422q2444r4677753p333r355511p1577p77776544q45552r2221p111r12566633p367û
2.9 Пусть p обозначает высказывание ("c1$c2g 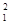 (c2, f
(c2, f 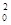 (c1, c2)))Ùg
(c1, c2)))Ùg  (f
(f  , f
, f  (c2))Þg
(c2))Þg  Úg
Úg  (c1). Индукцией по построению высказывания определить его истинностное значение на универсуме при такой интерпретации функциональных и предикатных знаков.
(c1). Индукцией по построению высказывания определить его истинностное значение на универсуме при такой интерпретации функциональных и предикатных знаков.
f 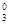
| g 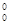
| X | f  (X) (X)
| g  (X) (X)
| X | Y | f 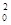 (X, Y) (X, Y)
| g  (X, Y) (X, Y)
| ||
| 3 | И | 3 | 4 | Л | 3 | 3 | 3 | И | ||
| 4 | 3 | И | 3 | 4 | 4 | И | ||||
| 4 | 3 | 4 | И | |||||||
| 4 | 4 | 4 | Л |
Ответ:
| c2 | p |
| 3 | Л |
| 4 | И |
2.10 Указать истинностные значения высказываний 2<2ÞХ>3, Х<3+4ÛХ<9, 7<Х<9ÞХ=8, Х£3ÚХ>3, "Х(Х>3)Þ5=3, $c1"c2(c2<c1), "c2$c1 (c2<c1) [ИПИИИЛИ].
2.11 Для каждого из правил Dp, q, r, pÙqÙr; Dp, pÞp; DpÞp, p; DpÚq, Øp, q; DØØØØp, p; Dp, $XP; D$XP, P; DP, "XP; D"XP; P выяснить является ли оно правилом вывода [ДДНДДДНДД].
2.12 Для каждого из высказываний g  (a), "X g
(a), "X g  (X,C), $X(g
(X,C), $X(g  Þ g
Þ g  ), $Xg
), $Xg  Þ g
Þ g  , g
, g 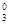 , Ø g
, Ø g  , g
, g  Û g
Û g 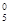 , g
, g 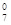 выяснить, является ли оно: предикатом [ДНННДННД], элементарным высказыванием [ДДДНДННД].
выяснить, является ли оно: предикатом [ДНННДННД], элементарным высказыванием [ДДДНДННД].
2.13 Для высказывания "X(g  Þ g
Þ g  (X))Úg
(X))Úg  записать: все его компоненты [g
записать: все его компоненты [g  , g
, g 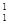 (X), g
(X), g  Þg
Þg  (X), "X(g
(X), "X(g  Þg
Þg  (X)), "X(g
(X)), "X(g  Þ g
Þ g  (X))Úg
(X))Úg  ], все его элементарные компоненты, все его пропозициональные компоненты [g
], все его элементарные компоненты, все его пропозициональные компоненты [g  , "X(g
, "X(g  Þg
Þg  (X))], все его предикатные компоненты [g
(X))], все его предикатные компоненты [g  , g
, g  (X)].
(X)].
2.14 Записать все пропозициональные компоненты высказываний $XPÙ$ZP, $XPÙØ$ZP. [$XP, $ZP – если X, Z различные переменные, $cnP – если X, Z обозначают одну и ту же переменную cn].
|
|
|
3.1 Вычислить:
ИÚØЛÞИÞЛÙИÛИÛЛÚИÚЛÚØИÞЛÙИÙЛÙØИÙØЛÙИÙЛÙØИÙИÙЛ
[И].
3.2 Выяснить, является ли высказывание ØpÙqÙ(rÞs)Û(pÚØqÚrÙØs) тавтологией [Д].
3.3 Пусть p, q, r – различные элементы высказывания. Для каждого из высказываний pÞØrÚqÚp, pÞØr, rÞØpÚq выяснить, является ли оно тавтологией [ДНН] и является ли оно тавтологическим следствием двух других [ДНД].
3.4 Решить истинностное уравнение (pÞq)ÞØqÞp= Л с двумя неизвестными p, q [Л, Л].
3.5 Из p, q, r составить высказывание, истинное только при p=q=r
[(pÛq) Ù(qÛr)].
4.1 Пусть Р обозначает g  (x). Для каждого из высказываний pÞ$XP, $XPÞ P, $XPÞØP выяснить является ли оно кванторологически истинным [ДНН] и является ли оно кванторологическим следствием двух других [ДДН].
(x). Для каждого из высказываний pÞ$XP, $XPÞ P, $XPÞØP выяснить является ли оно кванторологически истинным [ДНН] и является ли оно кванторологическим следствием двух других [ДДН].
4.2 Для каждого вхождения переменной в высказывание из задачи 2.9 выяснить, является ли оно свободным или связанным [связанное, связанное, связанное, связанное, свободное, свободное].
4.3 Записать обозначенное через "c3g  (c3, c4) íc4,¦
(c3, c4) íc4,¦ 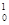 (c3)ý высказывание ["c3g
(c3)ý высказывание ["c3g  (c3, ¦
(c3, ¦ 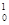 (c3))].
(c3))].
4.4 Пусть P обозначает высказывание $c3g  (c6, c3)Ú "c6g
(c6, c3)Ú "c6g  (c6, c3) Ú g
(c6, c3) Ú g  (c6, c4).
(c6, c4).
Указать высказывания с обозначениями P íc3, c6ý, P íc3, ¦ 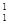 (c5)ý, P íc3, c3ý. [$c3g
(c5)ý, P íc3, c3ý. [$c3g  (c6, c3)Ú "c6g
(c6, c3)Ú "c6g  (c6, c6) Ù g
(c6, c6) Ù g  (c6, c6), $c3g
(c6, c6), $c3g  (c3, c3)Ú "c6g
(c3, c3)Ú "c6g  (c6, c3) Ù g
(c6, c3) Ù g  (c3, c3), P, P].
(c3, c3), P, P].
4.5 Для каждого из терминов ¦  (c1), ¦
(c1), ¦  (c2), ¦
(c2), ¦  (c8), ¦
(c8), ¦  (c1, c5, c8), ¦
(c1, c5, c8), ¦  выяснить, является ли он допустимым заменителем для c8 в высказывании $c2g
выяснить, является ли он допустимым заменителем для c8 в высказывании $c2g 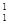 (c8)Ú "c5g
(c8)Ú "c5g  (c8) [ДНДНД].
(c8) [ДНДНД].
4.6 Для каждого из высказываний [$c1g  (c1), "c2g
(c1), "c2g 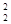 (c2, c3), g
(c2, c3), g 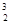 (c1, c2, c3), g
(c1, c2, c3), g 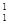 (¦
(¦  ) выяснить, является ли оно замкнутым [ДННД] и является ли оно открытым [ННДД].
) выяснить, является ли оно замкнутым [ДННД] и является ли оно открытым [ННДД].
4.7 Высказывание Ø"C$Z(C£ZÛZ¹0ÙØ$C(C>Z))Þ$C"Z(C³Z) привести к позитивной форме
[$C"Z(C>ZÙZ¹0Ù"C(C£Z)ÚC£ZÙ(Z=0Ú$C(C>Z)))Þ"C$Z(C<Z)].
4.8 В высказывании $c3g  (c3, c5)ÚØ" c5g
(c3, c5)ÚØ" c5g  (c3, c5) Þ g
(c3, c5) Þ g  Ûg
Ûg  (¦
(¦  , c5) второе вхождение высказывания g
, c5) второе вхождение высказывания g  (c3, c5) заменить высказыванием Ø g
(c3, c5) заменить высказыванием Ø g  (c3, c5) Þ g
(c3, c5) Þ g  (c3, c5). [$c3g
(c3, c5). [$c3g  (c3, c5)ÚØ" c5(Ø g
(c3, c5)ÚØ" c5(Ø g  (c3, c5) Þ g
(c3, c5) Þ g  (c3, c5) Þ g
(c3, c5) Þ g  Ûg
Ûg  (¦
(¦  , c5) и выяснить, равносилен ли результат замены исходному высказыванию [Д].
, c5) и выяснить, равносилен ли результат замены исходному высказыванию [Д].
5.1 Для каждого из высказываний g 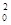 (¦
(¦ 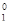 , ¦
, ¦ 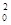 ), $c1g
), $c1g 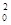 (c1, c2), g
(c1, c2), g 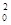 (¦
(¦ 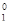 , ¦
, ¦  )Ùg
)Ùg 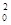 (¦
(¦  , ¦
, ¦  ) выяснить, является ли оно логически истинным [НДН] и является ли оно логическим следствием остальных [ДДН].
) выяснить, является ли оно логически истинным [НДН] и является ли оно логическим следствием остальных [ДДН].
5.2 Указать высказывания p, q т.ч. p½=q, но pÞq не есть логически истинное высказывание [c1= c2, c1= c3].
6.1 Выяснить, является ли последовательность высказываний P, PÞ$CR, $CR, PÞ$CRÞR, $CRÞR, $CRÞ"CR, "CR, R=QÞRÙQ, Q, RÙQ доказательством в теории с аксиомами R,Q [Д].
|
|
|
6.2 Для каждого из высказываний 3<5, 5=5, Х<6Þ$C(C<6), 5<6Þ5<6 выяснить, является ли оно: истинным [ДДДД], логически истинным [НДДД], кванторологически истинным [ННДД], тавтологически истинным [НННД].
6.3 Для каждого из высказываний g 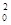 (c1, c2), $c1g
(c1, c2), $c1g  (c1), g
(c1), g 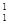 (c1) выяснить, является ли оно из двух других: логическим следствием [НДД], кванторологическим следствием [НДН], тавтологическим следствием [ННН].
(c1) выяснить, является ли оно из двух других: логическим следствием [НДД], кванторологическим следствием [НДН], тавтологическим следствием [ННН].
6.4 Записать определяющие аксиомы в формальной арифметике для термов ½c1- c2½,6. [c1+½c1- c2½=c2Úc2+½c1- c2½=c1, 6=(((((1)+(1))+(1))+(1))+(1)] и для высказываний: c1 есть четное число, c1, есть простое число, c1, есть делитель числа c2. [$c3=c3 + c3), Ø$c3$c4(c3×c4 Ùc3<c1Ùc4<c1) Ù1<c, Øc1=0Ù$c3(c2=(c1×c3)].
7.1 Пусть A, D, C, D, E, F, G, X, Y, Z, X1,..., Xn обозначают попарно различные переменные. Указать истинное значение каждого из высказываний 5Î{3,5}, 3Ï{3,5}, 4Ï{3,5}, {3,5}¹{5,3}, {3,5}={3,3,5}, {2,8}Ì{2,9,8}, {2,9,8}Ì{2,8}, 4Î{4}, 4Ì{4}, {4}Î4, 4¹4, {4}Ì{4}, {4}¹4, {6}Ï{2,6}, {2Х½Х=3ÚХ=4}={6,8}, {Х½Х¹Х}=Æ, {4,3}È{3,7}={4,3,7}, {4,3}Ç{3,7}={3}, {4,3}\{3,7}={4}, {3,5}È{5,3}¹{3,5}, A=BÛ"C(CÎAÛCÎB), CÏAÛØCÎA, AÎA, CÎÆ, AÌBÛ"C(XÎAÞCÎB), AËBÛØAÌB, AÌBÙBÌCÞAÌC, AËA, ÆËA, AÌAÈB, AÈBÌA, AÇBÌA, AÌAÇB, AÈƹA, AÇƹÆ, (AÈB)ÈC=AÈ(BÈC), AÈB¹AÈB, AÇB=BÇA, AÈA¹A, A¹BÛ$C(CÎAÙCÎBÚCÏAÙCÎB), AËBÛ$C(CÎAÙCÏB), (AÈB)\B=A, (A\B)\B=A\B, A\B=A(AÈB), A\(AÇB=A\B, A\B=B\A, AÇA¹A, AÌBÛAÈB=B, CÎ{C1,...,Cn}ÛC=C1Ú...ÚC=Cn, CÎAÈBÛCÎAÚBÎB, CÎAÇBÛCÎAÙBÎB, AÌBÞBÌA, A\A¹Æ, A\ƹA, AÌA, NÌZ, ZÌR, ZËN, RËZ, (2,2)=(2,2,2), (3,5)=(3,2+3), (3,5)=(5,3), {3,5}={5,3}, (4,8) ¹(8,4), (A,B)=(C,D)ÛA=CÙB=D, koor 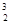 (8,5,4)=5, koor
(8,5,4)=5, koor 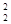 (8,5,4)=4, koor
(8,5,4)=4, koor  (8,5,4)=(8,5), koor
(8,5,4)=(8,5), koor  (8,5,4)=8, (X,Z) ¹(Z,X), (X,Z) ¹(Z,X) ÛX¹Z, koor
(8,5,4)=8, (X,Z) ¹(Z,X), (X,Z) ¹(Z,X) ÛX¹Z, koor  (a, b), koor
(a, b), koor 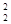 (a, b)=(a, b), (a, b)=(b, a), (a, a)=a, {4,6}х{7,9}={4,7), (4,9), (6,7), (6,9)}, {5} х {3,2} х {6}={(5,3,6), (5,2,6)}, {5} х {6}={6} х {5}, A х B=B х A, A х B¹B х A, A х (B х C)=(A х B) х C, (A х B) х C=A х B х C, A1=A, A2=A х A, A3=A х A х A,
(a, b)=(a, b), (a, b)=(b, a), (a, a)=a, {4,6}х{7,9}={4,7), (4,9), (6,7), (6,9)}, {5} х {3,2} х {6}={(5,3,6), (5,2,6)}, {5} х {6}={6} х {5}, A х B=B х A, A х B¹B х A, A х (B х C)=(A х B) х C, (A х B) х C=A х B х C, A1=A, A2=A х A, A3=A х A х A,
{8,5}2={(8,8), (8,5), (5,5)}, {6}4={(6,6,6,6)}, p 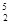 (A*D*C*D*E)=B, p
(A*D*C*D*E)=B, p 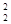 ({a, b)}¹b, p
({a, b)}¹b, p  {(3,7), (3,8), (3,9), (4,9)}={3,4}, p
{(3,7), (3,8), (3,9), (4,9)}={3,4}, p 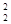 {(3,7), (3,8), (3,9), (4,9)}= {7,8,9}, p
{(3,7), (3,8), (3,9), (4,9)}= {7,8,9}, p  {(6,7,8,9)}=8, dom {(3,6), (6,4)}= {3,6,4}, dom {(3,6), (6,4)}= {3,6}, ran {(3,6), (6,4)}= {6,4}, ran {(3,6)} ¹6, {5,4,8} есть область определения функции {(5,5), (8,0). (4,)0}, есть образ множества {3} относительно функции {(3,7)}, dom sin =R, ran sin={X½RÎÙ½C½£1}, dom sin =dom tg, dom Arcsin=ransin, dom arcsin=R, ran arcsin=R,, функция sin биективна, cos(0)=1, функция sin и arcsin обратны друг другу, функция sin однозначна, функция arcsin однозначна, функция arcsin биективна, {(5,9), (5,8) (2,9)} есть расширение функции {(2,9)}, arcsin есть сужение функции Аrcsin, {(4,5), (5,8)} есть сужение функции {(4,7), (5,9) (5,8)}, функция {(4,4), (5,5)} биективна, функция sin È cos является многозначной. [1010110100011011111011001110101П1П00101011П1П1П0111111П00111110101111111П11П0110ПП011111110111011010110101011010110011]
{(6,7,8,9)}=8, dom {(3,6), (6,4)}= {3,6,4}, dom {(3,6), (6,4)}= {3,6}, ran {(3,6), (6,4)}= {6,4}, ran {(3,6)} ¹6, {5,4,8} есть область определения функции {(5,5), (8,0). (4,)0}, есть образ множества {3} относительно функции {(3,7)}, dom sin =R, ran sin={X½RÎÙ½C½£1}, dom sin =dom tg, dom Arcsin=ransin, dom arcsin=R, ran arcsin=R,, функция sin биективна, cos(0)=1, функция sin и arcsin обратны друг другу, функция sin однозначна, функция arcsin однозначна, функция arcsin биективна, {(5,9), (5,8) (2,9)} есть расширение функции {(2,9)}, arcsin есть сужение функции Аrcsin, {(4,5), (5,8)} есть сужение функции {(4,7), (5,9) (5,8)}, функция {(4,4), (5,5)} биективна, функция sin È cos является многозначной. [1010110100011011111011001110101П1П00101011П1П1П0111111П00111110101111111П11П0110ПП011111110111011010110101011010110011]
Для A=BÞ"C(ÎAÞCÎB) построить доказательство [(X=CÙA=BÞCÎAÞCÎB)Þ(C=CÞA=BÞCÎACÎB),C=CÙA=BÞCÎAÞCÎB,C=CÞA=BÞCÎAÞCÎB,C=C,A=BÞCÎAÞCÎB,A=BÞ"C(CÎAÞCÎB)]
|
|
|


