 |
Тема 5. Эгалитарная логика
|
|
|
|
или логика предикатов с равенством, т.е. с двухместным предикатным символом g20, который интерпретируется как знак равенства. Т.о. в эгалитарной логике предикат g20(a, b) выражает то, что мы привыкли выражать в виде a = b и понимать как констатацию того, что объекты с обозначениями a, b являются одинаковыми, равными, неотличимыми, идентичными. Эгалитарной интерпретацией формального языка называется такая, в которой g 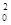 интерпретируется как знак равенства. Запись p1, …, pn│=q1, …, qm означает, что каждое из высказываний q1, …, qm является логическим следствием из высказываний p1, …, pn т.е. что оно является истинным в любой эгалитарной интерпретации, в которой оказываются истинными p1, …, pn. Высказывание p называется логически истинным, если │=p т.е. если p является истинным в любой эгалитарной интерпретации.
интерпретируется как знак равенства. Запись p1, …, pn│=q1, …, qm означает, что каждое из высказываний q1, …, qm является логическим следствием из высказываний p1, …, pn т.е. что оно является истинным в любой эгалитарной интерпретации, в которой оказываются истинными p1, …, pn. Высказывание p называется логически истинным, если │=p т.е. если p является истинным в любой эгалитарной интерпретации.
Правилами тождества, равенства, неотличимости называются следующие три правила соответственно:
Dg 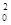 (x, x)
(x, x)
Dg 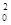 (x1, y1)Ù…Ù g
(x1, y1)Ù…Ù g 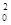 (xn, yn)Þg
(xn, yn)Þg 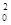 (f(x1, …, xn), f(y1, …, yn))
(f(x1, …, xn), f(y1, …, yn))
Dg2 (x1, y1)Ù…Ù g 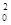 (xn, yn)Þ(g f(x1, …, xn)Þ(y1, …, yn))
(xn, yn)Þ(g f(x1, …, xn)Þ(y1, …, yn))
Теорема об эгалитарной замене: пусть q есть результат замены в p некоторых вхождений терма a термом b; тогда если выражение g20(a, b) является истинным, то p равносильно q.
Теорема о транзитивности логического следствия: если p1, …, pn│=q1, …, qm и q1, …, qm│= r1, …, re, то p1, …, pn│= r1, …, re.
Теорема о расширении списка гипотез: если p1, …, pn│= q, то p0, …, pn│= q.
Теорема дедукции: если высказывания p1, …, pn являются замкнутыми, то p1, …, pn│= p тогда и только тогда когда ê= p1Ù…Ù pnÞp.
Теорема о конъюнктивизации гипотез: p1, …, pn│= p тттк p1Ù…Ùpn│= p.
Теорема о выводе в эгалитарной логике: правила тавтологии, отделения, обобщения, подтверждения, общевнесения, сущевнесения, тождества, равенства, неотличимости образуют достаточный набор правил вывода в эгалитарной логике, т.е. p1, …, pn│= p тттк p может быть получено из p1, …, pn с помощью этого набора правил.
|
|
|
Теорема о сравнительной силе выводов. Если p является тавтологическим следствием из p1, …, pn, то p является кванторологическим следствием из p1, …, pn. Если p является кванторологическим следствием из р1,…,рn, то p является логическим следствием из р1,…,рn.
Алгоритм – это…
Теорема о неразрешимости проблемы логического следствия (логической истинности): нельзя придумать алгоритм, который для любых высказываний p0, …, pn позволял бы разрешить вопрос о том, является или нет p0 логическим следствием из p1, …, pn. Полезно обратить внимание на то, что проблема тавтологического следствия является разрешимой с помощью истинностных таблиц.
Замечание последние семь теорем не исключают случай n = 0.
Замечание если не оговорено противное, слово логика понимается как эгалитарная логика.
Тема 6. Формальные теории
предназначены для четкого изложения и развития тех или иных отраслей человеческих знаний. Задать формальную теорию – значит задать ее функциональные и предикатные символы, а также аксиомы, т. е. некоторые из высказываний, которые являются истинными в данной отрасли знаний. Развивать формальную теорию – значит пополнять запас ее теорем, т. е. таких высказываний, которые являются логическими следствиями аксиом.
Изложение любой формальной теории в принципе можно оформить в виде книжек с доказательными текстами:
| 1 | a1 - × - × - × - × - × - × - × - × - × - | ü индуктивная ý последовательность þ термов | ||
| … | ×××××××××××××××××××××××××××××××××××××××××××××××××××××× | |||
| k | ak - × - × - × - × - × - × - × - × - × - | |||
| k+1 | r1 - × - × - × - × - × - × - × - × - × - | ü индуктивная
ý последовательность формул þ на основе a1,…, ak | ||
| … | ×××××××××××××××××××××××××××××××××××××××××××××××××××××× | |||
| k+е | re - × - × - × - × - × - × - × - × - × - | |||
| k+е+1 | s1 - × - × - × - × - × - × - × - × - × - | ü аксиомы ý s1,…, sm есть þ среди r1,…, re | ||
| … | ×××××××××××××××××××××××××××××××××××××××××××××××××××××× | |||
| k+е+m | sm - × - × - × - × - × - × - × - × - × - | |||
| k+е+m+1 | t1 - × - × - × - × - × - × - × - × - × - | ü индуктивная ý последовательность теорем þ t1,…, tn есть среди r1,…, re | ||
| … | ×××××××××××××××××××××××××××××××××××××××××××××××××××××× | |||
| k+е+m+n | tn - × - × - × - × - × - × - × - × - × - |
Здесь штрих-пунктирная линия обозначает пояснение о том, с помощью какого правила порождения получено соответствующее знакосочетание. Для удобства таких пояснений знакосочетания a1,…, tn нумеруются последовательно от 1 до k+е+m+n. Вспомним, что правила порождения теорем являются правилами вывода, что конечная индуктивная последовательность теорем является доказательством и что следующие девять правил, называемых основными, образуют достаточный набор правил вывода из аксиом: правила тавтологии, отделения, обобщения, подтверждения, общевнесения, сущевнесения, тождества, равенства, неотличимости.
Такая форма изложения делает доказательство легко проверяемым, но практически не применяется из-за ее громоздкости.
Способы более компактного изложения формальной теории.
1. Последовательность a1,…, re не записывается, потому что при достаточном навыке термы и формулы распознаются без построения их индуктивных последовательностей.
|
|
|
2. В последовательность t1,…, tn включаются теоремы из других доказательных текстов.
3. Для двухместного функционального или предикатного знака v используется операционная форма записи: вместо v(a,b) пишут (a)v(b).
4. При операционной форме записи принимается соглашение об упразднении некоторых пар скобок в соответствии с соглашением об убывании силы связи в последовательности: одноместный функциональный знак, двухместный функциональный знак, одноместный предикатный знак, двухместный предикатный знак, логический знак.
5. Используются специальные начертания для функциональных и предикатных знаков. Например в теории чисел: 0, 1, 2, 3 - нульместные функциональные знаки; Ö, sin, cos - одноместные функциональные знаки; +, -, ´, /, - двухместные функциональные знаки; <, >, £, ³ - двухместные предикатные знаки.
6. Используются знаковые фигуры. Например, åх=3х обозначает сумму 3+4+5.
7. Вводится определяющая аксиома g(х1,...,х11)Û р для нового n-местного предикатного символа g. Здесь переменные х1,...,хn попарно различны, а высказывание р не имеет свободных вхождений переменных, отличных от х1,...,хn.
8. Вводится определяющая аксиома р{х, ¦(х1,...,хn)} для нового n - местного функционального символа ¦ в тех случаях, когда формула $рх является теоремой. Здесь переменные х, х1,...,хn попарно различны, а р не имеет свободное вхождение переменных, отличных от х, х1,...,хn.
Теорема об определениях: если теория Т2 получена из теории Т1 путем добавления определяющей аксиомы для нового функционального или предикатного символа v то для каждой теоремы теории Т2 существует равносильная ей теорема теории Т1.
9. Кроме девяти основных применяются дополнительные правила вывода, например правило отделения конъюнкта D pÙg, р и правило присоединения дизъюнкта Dр, pÚg.
10. Применяются известные методы доказательства. Обоснование таких методов дается в учебниках логики. Например метод доказательства от противного основан на следующей теореме.
|
|
|
Теорема о доказательстве методом от противного: если формальная теория Т2 получена путем добавления аксиомы Øр к аксиомам теории Т1 и если формулы q, Øq являются теоремами теории Т2, то формула р является теоремой теории Т1.
Формальная арифметика формализует систему знаний о целых неотрицательных числах, использует в качестве исходных четыре функциональных и два предикатных знака
¦ 
| ¦ 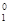
| ¦ 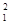
| ¦ 
| g 
| g 
|
| 0 | 1 | + | × | = | < |
интерпретируемых в соответствии с их известными со школы специальными начертаниями, имеет такие аксиомы
Ø1=0
х + 1= y + Þ x = y
x + 0 = x
x + (y + 1) = (x + y) + 1
x×0 = 0
x×(y + 1) = x×y + x
Øx < 0
x < y + 1 Û x < y Ú x = y
p íx, 0ýÚ"(pÞíx, x + 1ý)Þ p
Здесь при записи аксиом использованы ранее перечисленные соглашения о компактизации изложения и известное соглашение о том, что знак умножения связывает сильнее знака сложения. Если такие соглашения не принимать, то к примеру первую аксиому следовало бы записать в виде Ø(g  (¦
(¦  ,¦
,¦  )).
)).
Пример определяющих аксиом для новых нульместных функциональных знаков 2, 3, 4, 5 и новых двухместных предикатных знаков >, £,³,¹:
| 2 = 1 + 1 | c1>c2 Û c2<c1 |
| 3 = 2 + 1 | c1£c2 Û c1 < c2 Ú c1 = c2 |
| 4 = 3 + 1 | c1³c2 Û c1 > c2 Ú c1 = c2 |
| 5 = 4 + 1 | c1¹c2 Û Øc1 = c2 |
Заметим, что знак < можно было бы не включать в перечень исходных знаков формальной арифметики, а ввести его с помощью определяющей аксиомы c1<c2 Û $c3(Øc3 = 0 Ù c1+ c3 = c2).
Пример доказательного текста в формальной арифметике (k = 3, е = 6, m = 1, n = 3):
| 1 | ¦  ---------------------------------------------- ----------------------------------------------
| Константа |
| 2 | ¦ 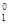 ----------------------------------- -----------------------------------
| Константа |
| 3 | c1 -------------------------------------------------- | Переменная |
| 4 | g  (¦ (¦ 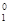 , ¦ , ¦  )--------------------------------------- )---------------------------------------
| Предикат от 2,1 |
| 5 | Ø(g  (¦ (¦ 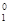 , ¦ , ¦ 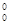 ))----------------------------------- ))-----------------------------------
| Отрицание 4 |
| 6 | g  (c1, ¦ (c1, ¦ 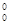 )---------------------------------------- )----------------------------------------
| Предикат от 3,1 |
| 7 | Ø(g  (c1, ¦ (c1, ¦ 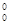 ))----------------------------------- ))-----------------------------------
| Отрицание 6 |
| 8 | $c1(g  (c1, ¦ (c1, ¦  )))-------------------------------- )))--------------------------------
| Подтверждение 7 по c1 |
| 9 | (Ø(g 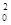 (¦ (¦ 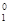 , ¦ , ¦ 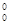 )))Þ$c1(Ø(g )))Þ$c1(Ø(g 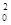 (c1, ¦ (c1, ¦ 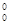 ))))---- ))))----
| Импликация 5,8 |
| 10 | Ø(g  (¦ (¦ 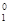 , ¦ , ¦ 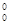 ))----------------------------------- ))-----------------------------------
| 5: аксиома |
| 11 | (Ø(g  (¦ (¦ 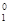 ,¦ ,¦ 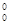 )))Þ$c1(Ø(g )))Þ$c1(Ø(g 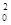 (c1,¦ (c1,¦  ))))---- ))))----
| 9: пр. подт. 7, c1, 2 |
| 12 | Ø(g  (¦ (¦  , ¦ , ¦  ))----------------------------------- ))-----------------------------------
| 5: аксиома 10 |
| 13 | $c1(Ø(g  (c1, ¦ (c1, ¦  )))---------------------------- )))----------------------------
| 8: пр. отделения для 12, 11 |
Компактизированный текст:
| 11 | Ø1 = 0 Þ$c1Øc1 = 0------------------------- | Правило подтверждения |
| 12 | Ø1 = 0-------------------------------------------- | Аксиома |
| 13 | $c1Øc1 = 0-------------------------------------- | Правило отд. для 12, 11 |
Словесный вариант: «Если единица не равна нулю, то тем самым существует не равное нулю число. Но единица не равна нулю. Следовательно, существует число, не равное нулю».
|
|
|
|
|
|


