 |
Задача 2. Б) Определите по графику, какого знака производная в точке В: . 1. отрицательная; 2. Нуль; 3. Положительная.
|
|
|
|
Задача 2.
На рисунке изображены график функции и касательные, проведенные к нему в точках с абсциссами А, В, С и Д.
А) Определите по графику, какого знака производная в точке А:
1. отрицательная; 2. Нуль; 3. Положительная.
Б) Определите по графику, какого знака производная в точке В:
1. отрицательная; 2. Нуль; 3. Положительная.
В) Определите по графику, какого знака производная в точке С:
1. отрицательная; 2. Нуль; 3. Положительная.
Г) Определите по графику, какого знака производная в точке Д:
1. отрицательная; 2. Нуль; 3. Положительная.
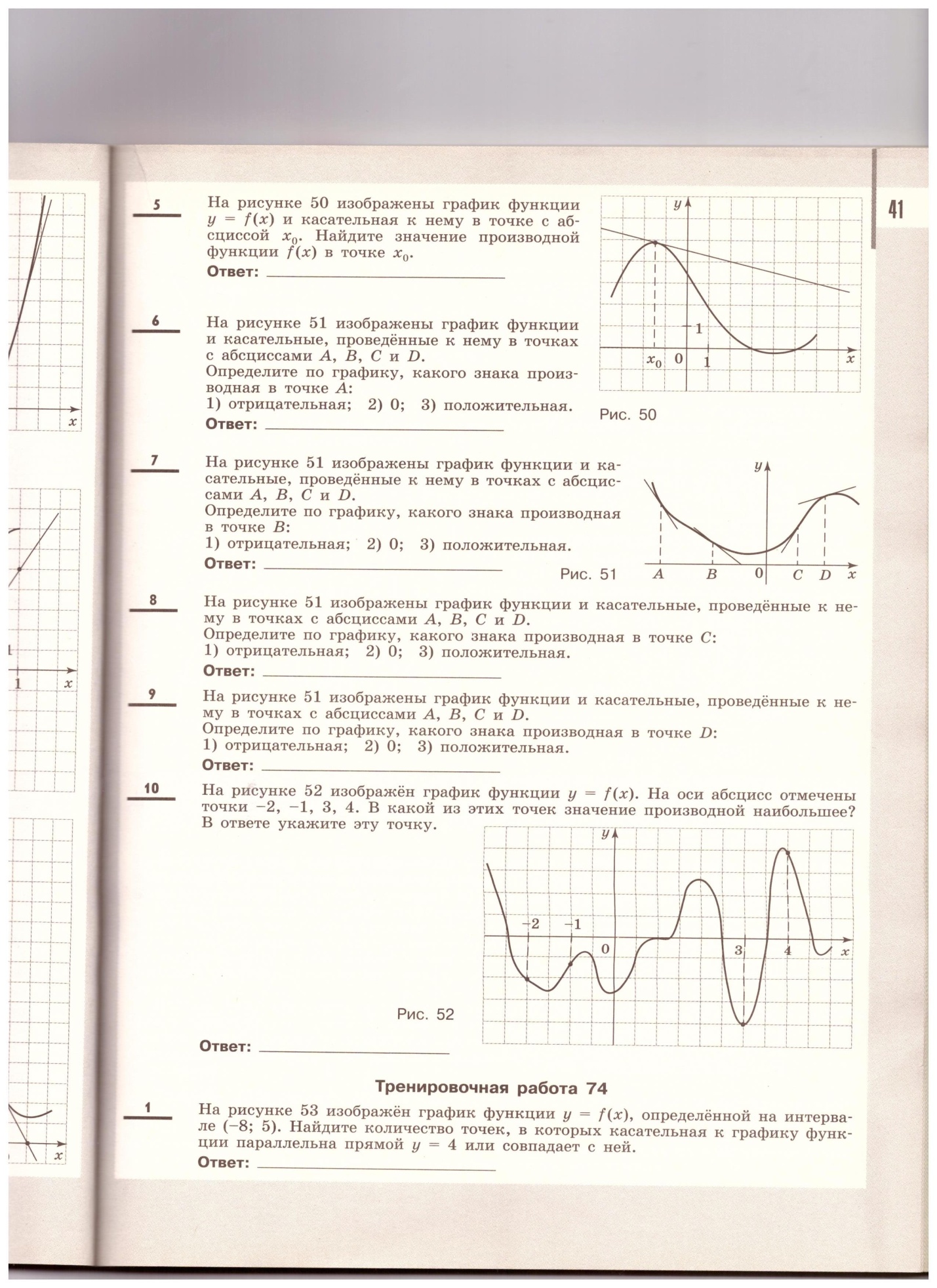
Задача 3.
На рисунке изображен график функции y=cosx
А) определите по графику значение cos 0
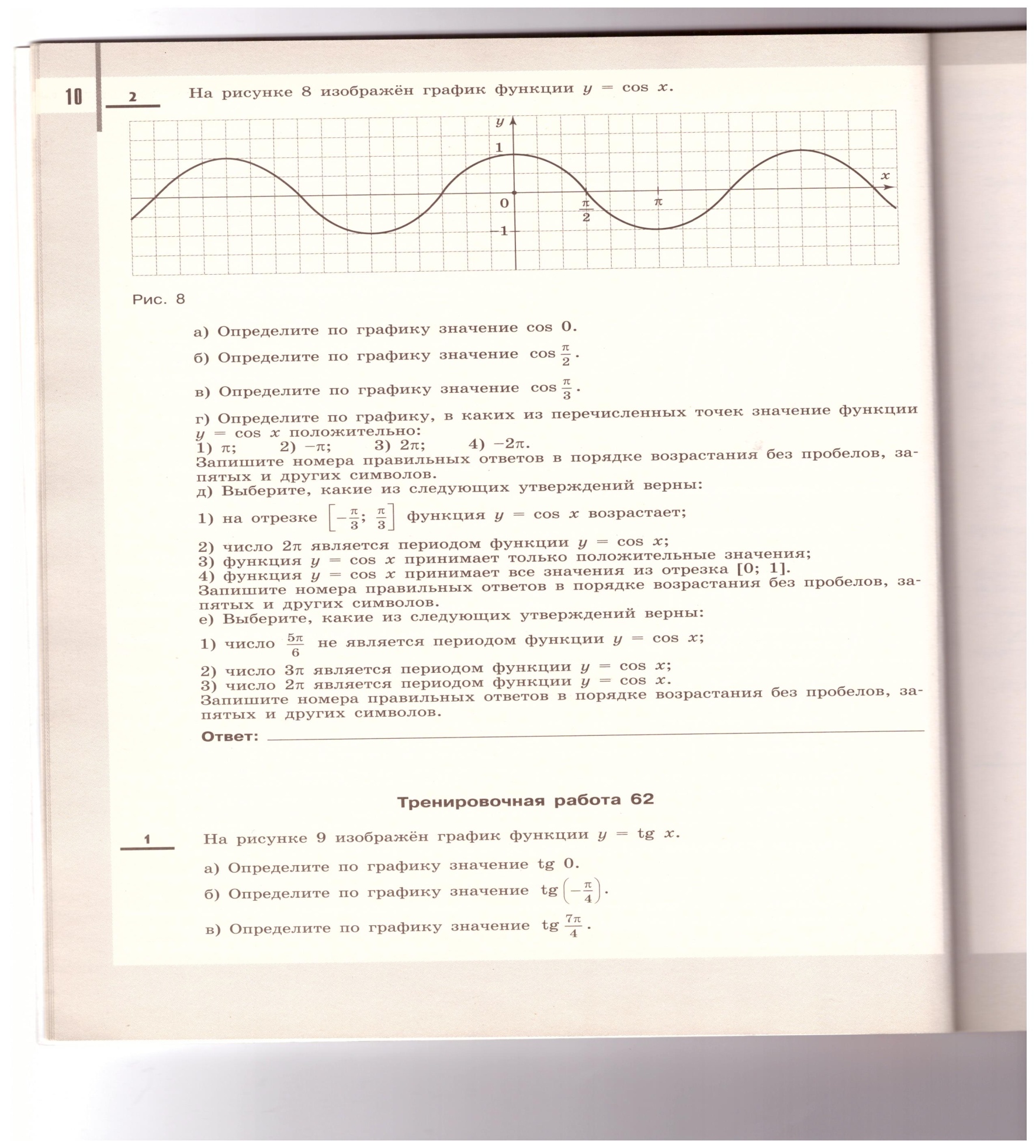
Б) определите по графику значение cos 
В) определите по графику значение cos 
Г) определите по графику, в каких из перечисленных точек значение функции y=cosx положительно:
1) π 2) –π 3) 2π 4) -2π. Запишите номера верных ответов в порядке возрастания.
Д) выберите, какие из следующих утверждений верны:
1) на отрезке [-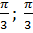 
] функция y=cosx возрастает;
2) число 2π является периодом функции y=cosx;
3) функцияy=cosx принимает только положительные значения;
4) функцияy=cosx принимает все значения из отрезка [ 0; 1].
Запишите номера правильных ответов в порядке возрастания.
Е) выберите, какие из следующих утверждений верные:
1) число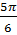 
не является периодом функции y=cosx;
2) число 3π является периодом функции y=cosx;
3) число 2π является периодом функции y=cosx;
Запишите номера правильных ответов в порядке возрастания.
Задача 4.
Алексей Юрьевич решил построить на дачном участке теплицу длиной
NP = 5, 5 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Алексей Юрьевич заказывает металлические дуги в форме
|
|
|
полуокружностей длиной 5, 8 м каждая и плёнку для обтяжки. В передней
стенке планируется вход, показанный на рисунке прямоугольником ACDB.
Точки A и B— середины отрезков MO и ON соответственно.
1) Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2) Найдите примерную ширину MN теплицы в метрах. Число π возьмите
равным 3, 14. Результат округлите до десятых.
3) Найдите примерную площадь участка внутри теплицы в квадратных метрах.
4) Сколько квадратных метров плёнки нужно купить для теплицы с учётом
передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3, 14. Ответ округлите до целых.
5) Найдите примерную высоту входа в теплицу в метрах. Число π возьмите
равным 3, 14. Ответ округлите до десятых.
Задача5. На рисунках изображены графики функций и касательные, проведенные к ним в точках с абсциссами х0. Установите соответствие между графиками функций и значениями производной этих в точках х0.
Значения производных:
1) -0, 2 2) -2, 5 3) 1. 5 4) 0, 25
В ответе запишите четырехзначное число.
Задача 6.
Знак «Крутой подъем», предусмотренный правилами дорожного движения, информирует водителя о приближении к подъему и о крутизне подъема, выраженной в процентах (число показывает, на сколько метров поднимается дорога в среднем на каждые 100м пути). Подъем обозначен знаком (см. рисунок). Пользуясь таблицей, определите примерно угол этого подъема в градусах.
Задача 7. В системе координат схематично изобразите график непрерывной функции y=f(x), которая удовлетворяет следующим свойствам:
1) Область определения функции – отрезок [-5; 5];
2) Функция четная;
3) На промежутке [0; 1]функция убывает;
4) В точке х=-3 функция принимает значение 4.
Задача 8. Про функцию f(x) известно, что:
1) f(x)-четная; 2) f(x)–периодическая, Т=12;
|
|
|
2) 3) f(x)=-х2+2х+3 при хЄ[0; 4]
3) 4) f(x)=4х-21 при хЄ(4; 6]
а) постройте график функции f(x)на отрезке
[-15; 6];
б) найдите число нулей функции на отрезке
[-15; 5].
Задача 9. На тригонометрической окружности отмечены точки Рa и Рβ , соответствующие углам a и β. Выберите верные утверждения.
1) sin a< sinβ
2) cos β -sin a > 0
3) cos β > cos a
4) cos a+sin β < 0
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных симолов.
Задача 10. 1. На рисунке изображен график функции f(x)=-sin 
Выберите верные утверждения:
1) функция f(x) возрастает на промежутке [-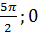 
]
2) функция f(x) убывает на промежутки [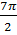 
; 5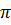 
]
3) число 4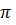 
является периодом функции f(x)
4) число 2 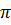является периодом функции f(x)
В ответе запишите номера выбранных утверждений без пробелов, запятых и других символов.
|
|
|
