Данные для расчета модели с фиктивной переменной

X
Y	13,3	8,9	15,1	10,4	13,1	12,4	13,2	11,8	11,5	14,2	15,4
Z

Если бы мы построили регрессию Y на X, то получили бы такое уравнение

Y =0,442+0,465 X.

Воспользовавшись моделью с фиктивной переменной получим

Y =0,643+0,466 X -0,422 Z

или для различных стран:

Y _K =0,221+0,466 X для Канады и Y _A=0,643+0,466 X для Америки.

Экспериментальные данные и три прямые, подобранные методом наименьших квадратов, приведены на рис. 4.3. Все три линии практически параллельны.

Дисперсионный анализ показывает значимость полученных зависимостей, причем уравнение (как с фиктивной переменной, так и без фиктивной переменной) объясняет до 80% вариации относительно среднего.

Вывод, который можно сделать в этом случае - введение фиктивной переменной не дает весомого улучшения модели в смысле дополнительно объясненной вариации.Ñ

Ясно, что для какой-либо задачи существует не единственный способ выбора фиктивных переменных, а в большинстве случаев путей их представления много. Это обстоятельство оказывается выгодным, поскольку в некоторых случаях можно угодить в ловушку, когда существует линейная зависимость между введенными фиктивными переменными.

Чтобы избежать ловушки, необходимо выбрать одну из категорий в качестве эталонной и определять фиктивные переменные для остальных возможных категорий, причем выбор эталонной категории не влияет на сущность регрессии.

 

Рис. 4.3

 

Может потребоваться включение в модель более одной совокупности фиктивных переменных. Это особенно часто встречается при работе с перекрестными выборками. Поясним такую процедуру – множественных совокупностей фиктивных переменных – на примере8.

Пример. Предположим, что исследуется зависимость между весом новорожденного и семейным положением матери, а также рожала ли она раньше.

Введем фиктивную переменную M, которая принимает значения 1, если мать одинока, и 0 – в остальных случаях.

Введем также фиктивную переменную числа родов в прошлом D, равную 1 для матерей, которые рожали в прошлом, и 0 для матерей, которые ранее не рожали.

При этом двойном наборе фиктивных переменных имеется четыре возможных случая с соответствующими комбинациями значений фиктивных переменных:

1. Замужняя мать, первые роды M =0, D =0.

2. Одинокая мать, первые роды M =1, D =0.

3. Замужняя мать, не первые роды M =0, D =1.

4. Одинокая мать, не первые роды M =1, D =1.

Первый случай по смыслу является основной совместной эталонной категорией. Коэффициент при M будет представлять оценку разности веса новорожденных, если мать одинока (ожидаем отрицательный знак коэффициента). Коэффициент при D будет представлять оценку дополнительного веса при рождении, если ребенок не является первенцем. Ребенок для четвертой категории матерей будет подвержен обоим воздействиям. Ñ

Фиктивные переменные могут быть введены не только в правую часть регрессионного соотношения, но и зависимая переменная может быть представлена в такой форме. Это возможно в тех случаях, когда в качестве зависимой переменной мы рассматриваем ответы на вопросы, пользуется ли человек собственной машиной, имеет ли счет в банке и т.п., причем во всех случаях зависимая переменная принимает дискретные значения.

Фиктивные переменные могут быть использованы для учета взаимодействия между различными группами факторов.

Пример. Проиллюстрируем сказанное на примере с окорочками. Для построения двух прямых рассмотрим модель:

Y = b ₀+ b ₁ X + Z (g ₁+ g ₂ X)+ u или Y = b ₀+ b ₁ X + g ₁ Z + g ₂ XZ + u.

Такой подход позволяет проверить различные варианты гипотез:

1. Гипотеза H₀: g ₁= g ₂=0 против альтернативы H₁: что это не так. Если гипотеза H₀ будет отвергнута, то мы придем к выводу, что модели не одинаковы, а если нет, то можно пользоваться одной моделью независимо от происхождения окороков.

2. Если гипотеза H₀ в предыдущем пункте будет отвергнута, то можно проверить гипотезу H₀: g ₂=0. Если H₀ принимается, то мы заключаем, что имеющиеся два набора данных отличаются только уровнем, имея одинаковые углы наклона.

При необходимости могут быть выбраны и другие варианты проверок, если это разумно для задачи. Получим для указанной выше модели уравнение МНК:

Y =2,974+0,377 X -3,649 Z +0,123(XZ),

причем R ²=0,82.

Два отдельных уравнения для Z =1: Y =-0,675+0,5 X;

и для Z =0: Y =2,974+0,377 X.

Как видно, уравнения несколько отличаются от тех линий, что приведены на рис. 4.3.

Для проверки гипотезы H₀: g ₁= g ₂=0 составим таблицу дисперсионного анализа (табл. 4.6). Значение F =3,399/0,983=3,458, что меньше F _0,05(2; 7)=4,74, а, следовательно, гипотеза H₀ принимается, то есть можно пользоваться одной моделью как для окороков из Америки, так и из Канады. Последнее подтверждается ранее полученными результатами.

Как показывает пример, использование взаимодействия с фиктивными переменными упрощает построение подходящих критериев и получение правильных статистик для проверки гипотез. Ñ

 

Таблица 4.6

Источник вариации	Сумма квадратов	Степени свободы	Средний квадрат
X	24,447		10,414
Z, XZ	6,797		3,399
Остаток	6,881		0,983
Всего	38,125

 

Часто эконометрист сталкивается с ситуацией, когда к уже имеющейся выборке он хочет присоединить небольшую дополнительную порцию данных, но не знает, можно ли считать выборки регрессионно однородными.

Если необходимо выяснить, можно ли использовать одну и ту же модель для двух разных выборок данных или следует оценивать отдельные регрессии для каждой выборки, то можно воспользоваться тестом Чоу.

Рассмотрим модели:

(4.14)

(4.15)

Мы хотим проверить гипотезу

H₀: ,

которая содержательно означает, что для двух имеющихся выборок из n ₁ и n ₂ наблюдений можно использовать одну и ту же регрессионную модель, т.е. выборки можно объединить.

Процедура Чоу для статистической проверки гипотезы H₀ суть:

1. Строим МНК оценки регрессии (4.14) и вычисляем сумму квадратов остатков, которую обозначим 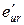. Строим МНК оценки регрессии (4.15) и вычисляем сумму квадратов остатков, которую обозначим .

2. Строим МНК оценки регрессии по объединенной (общей) выборке, содержащей в себе все наблюдения (числом n ₁+ n ₂) обеих выборок и вычисляем сумму квадратов остатков, которую обозначим e _r.

3. Критическая статистика F вычисляется по формуле:

и имеет распределение Фишера с (k +1) и (n ₁+ n ₂-2 k -2) степенями свободы. Если F > F_a, то нулевая гипотеза отвергается, и в этом случае мы не можем объединить две выборки в одну.

 

Временные ряды

Специфика временных рядов

Часто исследователь имеет дело с данными в виде временных рядов.

Совокупность наблюдений анализируемой величины , произведенных в последовательные моменты времени 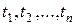, называется временным рядом.

Иначе говоря, временной ряд – это упорядоченная во времени последовательность наблюдений.

Среди временных рядов выделяют одномерные, полученные в результате наблюдения одной, фиксированной характеристики исследуемого объекта, и, многомерные временные ряды как результат наблюдений нескольких характеристик одного исследуемого объекта в течение ряда моментов времени.

По времени наблюдения временные ряды делятся на дискретные и непрерывные. Дискретные ряды, в свою очередь, разделяются на ряды с равноотстоящими и произвольными моментами наблюдения.

Временные ряды бывают детерминированными и случайными: первые получены как значения некоторой неслучайной функции, а вторые - как реализации случайной величины.

Стохастические временные ряды подразделяются на стационарные и нестационарные. Ряд y (t) называется стационарным (в узком смысле), если среднее, дисперсия и ковариации y (t) не зависят от t.

В дальнейшем, если не оговорено иначе, будем рассматривать одномерные, дискретные с равноотстоящими моментами наблюдений случайные временные ряды.

Природа временных рядов существенно отличается от природы пространственных данных, что проявляется в весьма специфических свойствах временных рядов. В своей работе исследователь должен учитывать эти особенности, основные из которых отображены в таблице 5.1.

Таблица 5.1

Особенности временных рядов

 

Характеристики наблюдений	Тип данных
Пространственные данные	Временные ряды
Порядок	Не существенен	Существенен
Статистическая независимость	Независимы	Не являются статистически независимыми
Функция распределения	Распределены одинаково	Распределены неодинаково
Количество	Как правило, большое	Как правило, небольшое
Наличие автокорреляции	Встречается нечасто	Встречается часто

 

Значения элементов временного ряда формируются под воздействием ряда факторов, среди которых выделяют:

· долговременные, формирующие в длительной перспективе общую тенденцию анализируемого признака. Эта тенденция описывается с помощью некоторой функции, называемой трендом (Т);

· сезонные, формирующие периодически повторяемые в определенное время года колебания анализируемого признака (S);

· циклические, формирующие изменения анализируемого в результате воздействия циклов экономической, демографической или астрофизической природы (С);

· случайные, не поддающиеся учету и регистрации, как результат воздействия случайных, внешних факторов (U).

Первые три составляющие часто объединяют в одну детерминированную и рассматривают модель ряда в виде y _t= f (t)+ u _t, " t. Изменение уровня f (t) со временем называют при этом трендом.

Предметом анализа временного ряда является выделение и изучение указанных компонент ряда, как правило в рамках одной из моделей ряда: либо аддитивной Y = T + C + S + U, либо мультипликативной Y = T × C × S × U.

Некоторые составляющие могут отсутствовать в тех или иных рядах.

В результате анализа временного ряда необходимо определить, какие из неслучайных составляющих присутствуют в разложении ряда, построить для них хорошие оценки, подобрать модель, описывающую поведение остатков и оценить ее параметры.

 

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: