 |
Коинтеграция и мнимая регрессия.
|
|
|
|
Рассмотрим два временных ряда y t и x t. Предположим, что оба ряда имеют единичные корни, то есть являются нестационарными. Предположим далее, что исследователь не знает механизмов, порождающих y t и x t, и оценивает регрессию:
y t = bx t + e t, t =1,…, n. (5.12)
Если e t = y t – bx t, t =1,…, n является стационарным временным рядом, то временные ряды y t и x t называются коинтегрированными, а вектор (1 – b) называется коинтегрирующим вектором.
Примеры.
1. Длинная ставка процента R, короткая ставка процента r: e t= R t – r t, вектор коинтеграции (1 –1).
2. Логарифм потребления C t, логарифм дохода y t: e t= С t – y t, вектор коинтеграции (1 –1).
3. Логарифм обменного курса D t, логарифм внутренней цены P t, логарифм цен мирового рынка P t*: e t= D t – P t+ P t*, вектор коинтеграции (1 –1 1). Ñ
В случае коинтегрируемости временных рядов говорят о долгосрочном динамическом равновесии. Если y t и x t коинтегрированы, то y t и bx t содержат общую нестационарную компоненту – долговременную тенденцию, а разность y t – bx t стационарна и совершает флуктуации около нуля.
Таким образом, коинтеграция временных рядов – причинно-следственная зависимость в уровнях временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости.
Возможен случай, когда ошибка e t = y t – bx t, t =1,…, n в регрессии (5.12) является нестационарным временным рядом. Тогда условия классической регрессионной модели (п. 3) не выполняются, в частности дисперсия e t не является постоянной. Кроме того, МНК оценка параметра b не состоятельна, поэтому с ростом объема выборки увеличиваются шансы получения ложных выводов о взаимосвязи y t и x t. Такая ситуация называется ложной (мнимой) регрессией. На практике признаками мнимой регрессии являются высокое значение R 2 и малое значение статистики Дарбина-Уотсона.
|
|
|
Для проверки рядов на коинтеграцию используются тесты Энгеля-Гранжера или Йохансена.
Пример. Рассмотрим временные ряды логарифмов доходов и расходов на потребление с августа 1990 г. по январь 1992 г. в России. Графический анализ – рис. 5.1 показывает, что тенденции этих рядов совпадают.
Расчет параметров уравнения регрессии логарифма расходов y t на логарифм доходов x t обычным МНК дает следующие результаты:
 =0,9 x t + e t,
=0,9 x t + e t,
n =25, R 2=0,80, критерий Дарбина-Уотсона 1,85, стандартная ошибка коэффициента регрессии 0,009.
Для тестирования рядов на коинтеграцию определим оценки остатков  =
=  - 0,9 x t и построим регрессию первых разностей D
- 0,9 x t и построим регрессию первых разностей D  на
на  :
:
D  = - 0,95
= - 0,95  .
.
Фактическое значение t-критерия для коэффициента последней регрессии равно –4,46, что превышает по абсолютной величине критическое значение 1,94, рассчитанное Энгелем и Гранжером, при уровне значимости 5%, т.е. с вероятностью 0,95 можно утверждать, что временные ряды логарифмов доходов и расходов на потребление коинтегрированы. Ñ
При изучении двух взаимосвязанных временных рядов на предварительной стадии регрессионного анализа рекомендуется устранить сезонные или циклические колебания, если они имеются в исследуемых временных рядах, в соответствии с принятой аддитивной или мультипликативной моделями рядов.
Если рассматриваемые временные ряды y t и x t содержат тенденцию, то коэффициент корреляции, характеризующий степень зависимости между y t и x t будет иметь высокое значение. Такая же ситуация будет иметь место тогда, когда y t и x t зависят от переменной времени t. Как в первом, так и во втором случае имеет место ложная корреляция, которая приводит при построении регрессии y t на x t вида (5.12) к автокорреляции в остатках и нестационарности ряда остатков регрессии (ложная регрессия), то есть к нарушению предпосылок МНК.
|
|
|

Рис. 5.13.
Для получения регрессии со стационарным временным рядом остатков e t, как уже указывалось ранее, может быть использован метод последовательных разностей, когда переход к некоторым k -м разностям уровней ряда позволяет получить стационарный ряд остатков.
Другими методами исключения тренда из анализируемой модели (5.12) являются методы включения фактора времени и отклонений от тренда.
Метод включения фактора времени.
Для устранения влияния времени на результат и факторы при изучении взаимосвязанных рядов динамики используется прием включения времени t в качестве независимой переменной в модель регрессии, что позволяет зафиксировать воздействие фактора t. Достоинством такого подхода является использование всей имеющейся выборки в отличие от метода последовательных разностей, который приводит к потере некоторого числа наблюдений.
Рассмотрим, например, модель вида:
y t = a + b 1 x t + b 2 t + e t,
которая относится к моделям c включенным фактором времени. Параметры модели определяются обычным МНК.
Пример. Потребительские расходы и доходы населения (тыс. у. е.) за ряд лет характеризуются следующими данными (табл. 5.13).
Таблица 5.13
| Показатель | Год | ||||||||
| Потребительские расходы | |||||||||
| Доходы |
Оценим уравнение регрессии потребительских расходов y t на доходы x t вида:
y t = a + bx t + e t.
Получим, применяя МНК:
y t = -5,38 + 0,92 x t + e t,
причем R 2=0,98, стандартная ошибка коэффициента b 1 при x t 0,04, статистика Дарбина-Уотсона 0,86. Т.е. имеем случай мнимой регрессии, когда статистика Дарбина-Уотсона показывает наличие положительной автокорреляции остатков e t, а коэффициент детерминации близок к единице.
Применяя метод включения фактора времени, оценим регрессию вида:
y t = a + b 1 x t + b 2 t + e t.
Получим, применяя МНК:
y t = 3,88 + 0,69 x t + 1,65 t + e t,
причем R 2=0,99, стандартная ошибка коэффициента b 1 при x t 0,11, статистика Дарбина-Уотсона 1,3.
Полученное уравнение имеет следующую интерпретацию. Значение параметра b 1=0,69, говорит о том, что при увеличении дохода на 1 тыс. у.е., потребительские расходы возрастут в среднем на 0,69 тыс. у.е., если существующая тенденция будет неизменна. Значение b 2=1,65 свидетельствует о том, что без учета роста доходов населения ежегодный средний абсолютный прирост потребительских расходов составит 1,65 тыс. у.е. Ñ
|
|
|
Метод отклонения уровней ряда от основной тенденции.
Если каждый из рядов y t и x t содержит тренд, то аналитическим выравниванием по каждому из рядов можно найти параметры тренда и определить расчетные по тренду уровни рядов  и
и  . Влияние тенденции можно устранить путем вычитания расчетных значений тренда из фактических. Дальнейший регрессионный анализ проводят с отклонениями от тренда
. Влияние тенденции можно устранить путем вычитания расчетных значений тренда из фактических. Дальнейший регрессионный анализ проводят с отклонениями от тренда  и
и  .
.
Пример. Потребительские расходы и доходы населения (тыс. у.е.) за ряд лет характеризуются данными табл. 5.13.
Рассчитаем линейные тренды по каждому из временных рядов методом МНК:
 =35,39+6,23 t, R 2=0,93 стандартная ошибка коэффициента при t 0,63,
=35,39+6,23 t, R 2=0,93 стандартная ошибка коэффициента при t 0,63,
 =45,33+6,60 t, R 2=0,89 стандартная ошибка коэффициента при t 0,85.
=45,33+6,60 t, R 2=0,89 стандартная ошибка коэффициента при t 0,85.
По трендам определим расчетные значения  и
и  и отклонения от трендов
и отклонения от трендов  и
и  .
.
Таблица 5.14
Тренды и отклонения от трендов для временных рядов доходов и потребительских расходов
| Время, t | y t | x t | 
| 
| 
| 
|
| 41,62 | 51,93 | 4,38 | 7,07 | |||
| 47,86 | 58,53 | 2,14 | 4,47 | |||
| 54,09 | 65,13 | -0,09 | -1,13 | |||
| 60,32 | 71,73 | -1,32 | -5,73 | |||
| 66,56 | 78,33 | -4,56 | -7,33 | |||
| 72,79 | 84,93 | -5,79 | -6,93 | |||
| 79,02 | 91,53 | -4,02 | -2,53 | |||
| 85,26 | 98,13 | 0,74 | 2,87 | |||
| 91,49 | 104,73 | 8,51 | 9,27 |
Проверим полученные отклонения от трендов на автокорреляцию. Коэффициенты автокорреляции первого порядка составляют:
 =0,56,
=0,56,  =0,67,
=0,67,
в то время как для исходных рядов  =0,99,
=0,99,  =0,99.
=0,99.
Таким образом, полученные ряды отклонений от трендов можно использовать для получения количественной характеристики связи исходных временных рядов потребительских расходов и доходов населения. Коэффициент корреляции по отклонениям от трендов равен 0,93, тогда как этот же показатель по начальным уровням ряда был равен 0,99. Связь между потребительскими расходами и доходами населения прямая и сильная.
Результаты построения модели регрессии по отклонениям от трендов следующие:
|
|
|
| Константа | 0,00 |
| Коэффициент регрессии | 0,69 |
| Стандартная ошибка коэффициента регрессии | 0,09 |
| R 2 | 0,88 |
| Статистика Дарбина-Уотсона | 1,30 |
Содержательная интерпретация модели в отклонениях от трендов затруднительна, но она может быть использована для прогнозирования. Ñ
Библиографический список
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. М.: ЮНИТИ, 1998. 1022 с.
2. Джонстон Дж. Эконометрические методы.- М.: Статистика, 1980. 432 с.
3. Доугерти К. Введение в эконометрику. М.: ИНФРА-М, 2001. 402 с.
4. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. М.: Финансы и статистика, 1986. 392 с.
5. Магнус Я.Р, Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело, 2000. 400 с.
6. Практикум по эконометрике/Под ред. И.И.Елисеевой. М.: Финансы и статистика, 2001. 192 с.
7. Эконометрика/Под ред. И.И. Елисеевой. М.: Финансы и статистика, 2001. 344 с.
8. Кремер Н., Путко Б. Эконометрика. М.: ЮНИТИ-ДАНА, 2002. 311 с.
3. Методические указания к решению типовых задач [7]
Указания к содержат примеры решения типовых задач и собственно типовые задачи по основным разделам курса. Подробный разбор решения типовых задач позволит студентам очной и заочной форм обучения лучше подготовится к сдаче как теоретической части зачета, так и к решению задач.
Задача1
"Парная регрессия и корреляция"
1.1. Краткие сведения из теории.
Построение поля корреляции производится по исходным данным о парах значений факторного и результативного признаков с соблюдением масштаба. На основе поля корреляции делаются выводы о возможной функциональной форме связи между факторным и результативным признаками.
Оценки  и
и 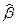 параметров a и b в уравнении парной линейной регрессии
параметров a и b в уравнении парной линейной регрессии  производится методом наименьших квадратов (МНК) из условия минимума суммы квадратов отклонений Yi от полученных по модели
производится методом наименьших квадратов (МНК) из условия минимума суммы квадратов отклонений Yi от полученных по модели  . Расчетные формулы:
. Расчетные формулы:
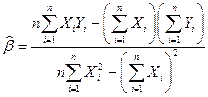 , (1)
, (1)
 , (2)
, (2)
где n – количество наблюдений в выборке, i = 1, …, n,  и
и  средние арифметические соответственно
средние арифметические соответственно 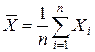 и
и  .
.
Коэффициент регрессии линейной функции 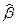 есть абсолютный показатель силы связи, характеризующий среднее абсолютное изменение результата при изменении факторного признака на единицу своего измерения.
есть абсолютный показатель силы связи, характеризующий среднее абсолютное изменение результата при изменении факторного признака на единицу своего измерения.
Линейный коэффициент корреляции характеризует тесноту линейной связи между изучаемыми признаками. Его можно определить по следующей формуле:
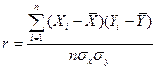 , (3)
, (3)
где s x и s y среднеквадратические отклонения для переменных X и Y соответственно  и
и  .
.
Значения линейного коэффициента корреляции принадлежит промежутку [-1; 1]. Чем ближе его абсолютное значение к 1, тем теснее линейная связь между признаками. Положительная величина свидетельствует о прямой связи между изучаемыми признаками, отрицательная – о наличии обратной связи между признаками.
|
|
|
Квадрат коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака. Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
Для проверки гипотезы о статистической значимости коэффициента регрессии формулируется нулевая гипотеза о том, что коэффициент регрессии статистически незначим: H0: b=0 (линейной зависимости нет) при конкурирующей гипотезе H1: b¹0 (линейная зависимость есть).
Фактическое значение критерия для проверки указанной гипотезы имеет t -распределение Стьюдента и рассчитывается по формуле:
 , (4)
, (4)
где mb - стандартная ошибка коэффициента регрессии, рассчитываемая как
 , (5)
, (5)
здесь  - оценка дисперсии случайных остатков регрессии
- оценка дисперсии случайных остатков регрессии  или с учетом формулы для ошибок регрессии
или с учетом формулы для ошибок регрессии  получим
получим
 . (6)
. (6)
Для определения табличного значения t e, n-2 пользуются таблицами распределения Стьюдента для заданного уровня значимости e, принимая во внимание, что число степеней свободы для t -статистики равно (n –2).
Далее сравнивают полученное фактическое значение с табличным. Если фактическое значение используемого критерия превышает табличное t > t e,n-2,то нулевая гипотеза отклоняется, и с вероятностью (1–e) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии. Если фактическое значение t -критерия меньше табличного t < t e, n-2 ,то оснований отклонять нулевую гипотезу нет.
Оценка статистической значимости построенной модели регрессии в целом производится с помощью F -критерия Фишера. В случае парной регрессии нулевая гипотеза формулируется как H0: b=0 при конкурирующей гипотезе H1: b¹0. Фактическое значение F -критерия может быть определено по формуле
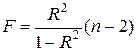 . (7)
. (7)
Для определения табличного значения F e;1;n-2 пользуются таблицами распределения Фишера для заданного уровня значимости e, принимая во внимание, что в случае парной регрессии число степеней свободы большей дисперсии равно 1, а число степеней свободы меньшей дисперсии равно (n −2).
Если F > F e; 1;n-2 , то нулевая гипотеза отклоняется, и с вероятностью (1–e) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии. Если F < F e; 1;n-2, то оснований отклонять нулевую гипотезу нет.
Отметим, что между значениями t и F, рассчитанных по формулам (4) и (7) соответственно, существует взаимосвязь  .
.
Для расчета точечного прогноза  необходимо подставить в уравнение регрессии заданное значение факторного признака X *, т.е.
необходимо подставить в уравнение регрессии заданное значение факторного признака X *, т.е.  .
.
Для расчета интервального прогноза построим доверительный интервал для значения  , лежащего на линии регрессии
, лежащего на линии регрессии
 , (8)
, (8)
где  .
.
Полученный интервал будет характеризовать значения результативного признака при заданном значении факторного признака X * для отдельной наблюдаемой единицы.
1.2. Пример решения типовой задачи.
Имеются данные о ежемесячном количестве посетителей и выручке крупных супермаркетов г. Ростова-на-Дону, приведенные ниже в таблице.
Задание.
1). Постройте поле корреляции результативного и факторного признаков.
2). Определите параметры уравнения парной линейной регрессии и дайте интерпретацию коэффициента регрессии b.
3). Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
4). С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии b и уравнения регрессии в целом. Сделайте выводы.
5). Рассчитайте прогнозное значение  для заданного X *=500 и постройте 95% доверительный интервал для прогноза.
для заданного X *=500 и постройте 95% доверительный интервал для прогноза.
| Супермаркет | Выручка за месяц, тыс. у.е., Y | Число посетителей за месяц, тыс. чел., X |
| Пять золотых | ||
| Солнечный круг - 1 | ||
| Арарат | ||
| Солнечный круг - 2 | ||
| Театральный | ||
| Пчелка | ||
| Пятый элемент | ||
| Северный | ||
| Вавилон - 2 | ||
| Западный | ||
| Вавилон - 1 | ||
| Рамстор |
Решение.
1). Для условия задачи поле корреляции выглядит следующим образом:

Между выручкой (Y) и количеством посетителей (X) визуально определяется прямая линейная зависимость.
2). Определим параметры уравнения парной линейной регрессии. Вычисления удобно организовать в таблицу. При этом сначала рассчитываются средние значения  и
и  по данным столбцов 2 и 3. Затем в столбцах 4 и 5 рассчитываются
по данным столбцов 2 и 3. Затем в столбцах 4 и 5 рассчитываются  ,
,  , i = 1, …, n, и в столбце 8 их произведение.
, i = 1, …, n, и в столбце 8 их произведение.
| N п/п | X | Y |

| 
|
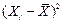
|

|
( )*
( )*
( ) )
| 
| e |
| -93 | -85,75 | 7353,06 | 7974,75 | 235,48 | 0,52 | ||||
| -75 | -67,75 | 4590,06 | 5081,25 | 252,18 | 1,82 | ||||
| -57 | -54,75 | 2997,56 | 3120,75 | 268,88 | -1,88 | ||||
| -41 | -40,75 | 1660,56 | 1670,75 | 283,72 | -2,72 | ||||
| -31 | -31,75 | 1008,06 | 984,25 | 292,99 | -2,99 | ||||
| -13 | -10,75 | 115,56 | 139,75 | 309,69 | 1,31 | ||||
| 3,25 | 10,56 | 321,75 | 3,25 | ||||||
| 13,25 | 175,56 | 185,5 | 334,74 | 0,26 | |||||
| 33,25 | 1105,56 | 1163,75 | 354,22 | 0,78 | |||||
| 53,25 | 2835,56 | 2928,75 | 372,77 | 2,23 | |||||
| 79,25 | 6280,56 | 6894,75 | 402,45 | -1,45 | |||||
| 109,25 | 11935,56 | 13000,75 | 432,13 | -1,13 | |||||
| Сум ма | 0,00 | 40068,25 | 0,00 | ||||||
| Сред нее | 350,0 | 321,75 |
По формуле (1) получим: 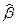 =43145/46510=0,93. По формуле (2) получим:
=43145/46510=0,93. По формуле (2) получим:  =321,75−0,93.350=−2,91.
=321,75−0,93.350=−2,91.
Оцененное уравнение регрессии запишется в виде  =−2,91+0,93 X.
=−2,91+0,93 X.
Интерпретация коэффициента регрессии. С увеличением числа посетителей на 1 тыс. человек выручка увеличится на 0,93 тыс.у.е.
3). Расчет линейного коэффициента корреляции проведем по формуле (3). С учетом вычислений в столбцах 6, 7 и 8 таблицы, получим:
r =43145/( )=0,99.
)=0,99.
Т.е. связь между изучаемыми переменными прямая (коэффициент корреляции положителен) линейная.
Определим коэффициент детерминации R 2=0,992=0,998. Т.е. 99,8% вариации выручки объясняется вариацией числа посетителей.
4). Оценим статистическую значимость коэффициента регрессии b.
Рассчитаем дисперсию ошибки регрессии по формуле (6) с учетом столбца 10 таблицы: 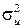 =44,76/(12-2)=4,476.
=44,76/(12-2)=4,476.
Рассчитаем стандартную ошибку коэффициента регрессии по формуле (5): mb=  =0,0098.
=0,0098.
Тогда по формуле (4) фактическое значение t статистики составит
t =0,93/0,0098=94,9.
По таблице находим для уровня значимости по условию 1−0,95=0,05 и числа степеней свободы 10: t 0,05;10=2,228. Поскольку t 0,05;10< t, то коэффициент регрессии b значим, т.е. наличие статистической связи между выручкой и числом посетителей супермаркетов статистически подтверждается.
Для проверки значимости уравнения регрессии в целом воспользуемся формулой (7):
F = 10.0,998/(1-0,998)=8935,4.
Поскольку табличное значение F распределения Фишера F 0,05;1;10=4,96 меньше расчетного, то гипотеза о статистической незначимости коэффициента регрессии должна быть отвергнута.
5). Рассчитаем прогнозное значение  для X *. Полученный интервал будет характеризовать значения результативного признака (выручки) при заданном значении факторного признака (числа посетителей) для отдельной наблюдаемой единицы. Построим точечный прогноз:
для X *. Полученный интервал будет характеризовать значения результативного признака (выручки) при заданном значении факторного признака (числа посетителей) для отдельной наблюдаемой единицы. Построим точечный прогноз:
 =−2,91+0,93.500=462,1.
=−2,91+0,93.500=462,1.
Построим 95% доверительный интервал для прогноза по формуле (8). Определим сначала
 =
= 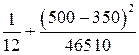 =0,567.
=0,567.
И, следовательно:
462,1±2,228  =462,1±5,9
=462,1±5,9
или 456,2£  £468.
£468.
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение выручки отдельного супермаркета, который за месяц посетят 500 тыс. чел. будет находиться в интервале от 456,2 до 468 тыс.у.е.
1.3. Задачи для самостоятельной работы.
1. Имеются данные о количестве копий (тыс. шт.), сделанных копировальными машинами различных марок в издательских центрах города и стоимости технического обслуживания копировальных машин (тыс. у. е.):
| Количество копий | ||||||||||||
| Стоимость техобслуживания | 1,4 | 1,6 | 1,7 | 1,75 | 1,85 | 2,4 | 2,7 | 2,8 | 2,8 | 2,7 | 2,9 | 3,0 |
К заданию 5) X *=21.
2. Имеются данные по 12 группам населения о среднегодовом доходе и уровне потребления мяса жителями штата Канзас (США):
| Среднегодовой доход в среднем по группе, тыс. дол. | 41,5 | 29,6 | 31,8 | 69,8 | 100,5 | 93,3 | 82,1 | 77,4 | 55,7 | 38,9 | 45,2 | 60,2 |
| Годовое потребление мяса на душу населения в среднем по группе, кг. | 41,2 | 35,3 | 40,7 | 55,1 | 80,1 | 65,9 | 64,2 | 70,5 | 61,1 | 51,7 | 59,4 | 65,8 |
К заданию 5) X *=51,4.
3. По однородным предприятиям имеются данные о количестве рабочих с профессиональной подготовкой и количестве бракованной продукции:
| № предприятия | ||||||||||
| Количество рабочих с проф. подготовкой, % | 39,4 | 40,1 | 48,6 | 54,7 | 58,4 | 70,5 | 85,1 | 65,3 | 57,3 | 50,6 |
| Количество бракованной продукции, % | 17,1 | 18,3 | 11,2 | 9,3 | 10,8 | 5,9 | 2,8 | 6,7 | 8,4 | 9,5 |
К заданию 5) X *=50,9.
4. Периодически в средствах массовой информации обсуждаются высокие должностные оклады президентов благотворительных организаций. Дана информация о десяти крупнейших филиалах общества United Way.
| Город | Должностной оклад президента, тыс. дол. | Собранная сумма пожертвований в расчете на душу населения, дол. |
| Атланта | ||
| Чикаго | ||
| Кливленд | ||
| Денвер | ||
| Детройт | ||
| Хьюстон | ||
| Канзас-Сити | ||
| Лос-Анжелес | ||
| Миннеаполис | ||
| Сиэтл |
К заданию 5) X *=26.
5. Компания «Вест», состоящая из 12 региональных представительств, продает кухонные принадлежности, рассылая каталоги по почте. Данные, иллюстрирующие количество рассылок (тыс. адресов) и объем выручки региональных представительств компании (млн. у. е.):
| Количество адресов рассылки, тыс. адресов | ||||||||||||
| Выручка, млн.у.е. | 17,5 | 24,5 | 29,5 | 18,5 |
К заданию 5) X *=100.
6. Данные о тираже бесплатной рекламной газеты «Реклама для вас», распространяемой в различных регионах РФ и стоимости размещения в ней рекламы стандартного размера (1/4 газетной полосы):
| Регион | Тираж, тыс.экз. | Стоимость рекламы, тыс.у.е. |
| Ростовская область | 1,6 | |
| Курская область | 1,2 | |
| Воронежская область | ||
| Московская область | 2,6 | |
| Ставропольский край | ||
| Хабаровский край | 1,3 | |
| Вологодская область | 0,8 | |
| Волгоградская область | 1,7 | |
| Рязанская область | 1,3 | |
| Красноярский край | 1,5 | |
| Иркутская область | 0,9 | |
| Томская область | 1,6 | |
| Тюменская область | 2,1 | |
| Краснодарский край | 2,2 | |
| Ленинградская область | 2,7 |
К заданию 5) X *=150.
7. Администрация страховой компании приняла решение о введении нового вида услуг − страхования на случай пожара. С целью определения тарифов по выборке анализируется зависимость стоимости ущерба, нанесенного пожаром, от расстояния до ближайшей пожарной станции:
| Общая сумма ущерба, млн. руб. | 25,0 | 38,9 | 68,1 | 75,4 | 91,4 | 55,3 | 40,7 | 79,3 | 88,8 | 19,1 |
| Расстояние до ближайшей пожарной станции, км. | 4,5 | 3,8 | 5,1 | 4,8 | 10,1 | 8,2 | 6,1 | 9,2 | 3,1 | 2,1 |
К заданию 5) X *=5,5.
8. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей и стоимостью ежемесячного обслуживания:
| Пробег, тыс. км | ||||||||||||
| Стоимость обслуживания, у.е. |
К заданию 5) X *=25.
9. Исследуется зависимость между урожайностью зерновых и количеством внесенных удобрений. Данные по 11 фермерским хозяйствам области:
| Урожайность зерновых ц/га | |||||||||||
| Внесено удобрений на 1 га посева, кг |
К заданию 5) X *=22.
10. При исследовании годового дохода и сбережений населения получены следующие данные:
| Доход, тыс. у.е. | ||||||||||
| Сбережения, тыс. у.е. |
К заданию 5) X *=100.
Задача 2
"Множественная регрессия и корреляция"
2.1. Краткие сведения из теории.
Пусть имеется n наблюдений над переменными Yi, X 1 i , X 2 i , i =1,…, n. Парные коэффициенты корреляции рассчитываются по формулам:
 , (9)
, (9)
 . (10)
. (10)
Частные коэффициенты корреляции между двумя переменными при фиксированном воздействии другой переменной рассчитываются через значения парных коэффициентов корреляции. Коэффициент частной корреляции между Y и X 1, когда X 2 является константой:
 . (11)
. (11)
Коэффициент частной корреляции между Y и X 2, когда X 1 является константой:
 . (12)
. (12)
Коэффициент частной корреляции между X 1 и X 2, когда Y является константой:
 . (13)
. (13)
Классическая линейная модель множественной регрессии записывается в виде:
 (14)
(14)
где u – случайная величина ошибки.
Применение МНК к (14) позволяет получить формулы для оценок коэффициентов:
 ,
,  ,
,  , (15)
, (15)
где  ,
,  и
и  среднеквадратические отклонения для переменных Y, X 1 и X 2 соответственно
среднеквадратические отклонения для переменных Y, X 1 и X 2 соответственно  ,
,  и
и  , а
, а  ,
, 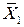 и
и  средние арифметические для переменных Y, X 1 и X 2 соответственно.
средние арифметические для переменных Y, X 1 и X 2 соответственно.
Параметры регрессии 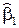 и
и  это показатели, характеризующие абсолютное (в натуральных единицах измерения) изменение результативного признака при изменении соответствующего факторного признака на единицу своего измерения при фиксированном влиянии другого фактора.
это показатели, характеризующие абсолютное (в натуральных единицах измерения) изменение результативного признака при изменении соответствующего факторного признака на единицу своего измерения при фиксированном влиянии другого фактора.
Значение коэффициента детерминации (квадрат коэффициента множественной корреляции) получается по формуле:
 . (16)
. (16)
Скорректированный на число степеней свободы коэффициент детерминации для модели (14) равен:
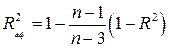 . (17)
. (17)
Для проверки статистической значимости построенной модели регрессии в целом используется F -критерий Фишера. В случае регрессии (14) нулевая гипотеза формулируется как H0:  при конкурирующей гипотезе H1:
при конкурирующей гипотезе H1:  ,
,  . Фактическое значение F -критерия может быть определено по формуле
. Фактическое значение F -критерия может быть определено по формуле
 . (18)
. (18)
Для определения табличного значения F e; 2; n-3 пользуются таблицами распределения Фишера для заданного уровня значимости e, принимая во внимание, что число степеней свободы большей дисперсии равно 2, а число степеней свободы меньшей дисперсии равно (n −3).
Если F > F e; 2; n-3 , то нулевая гипотеза отклоняется, и с вероятностью (1–e) принимается альтернативная гипотеза о статистической значимости регрессии. Если F < F e; 2; n-3 , то оснований отклонять нулевую гипотезу нет.
Расчет относительных показателей силы связи в уравнении множественной регрессии, частных коэффициентов эластичности, производится по формуле:
 , j=1,2. (19)
, j=1,2. (19)
Частные коэффициенты эластичности Эj показывают, на сколько процентов от значения своей средней  изменяется результат при изменении фактора Xj на 1% от своей средней
изменяется результат при изменении фактора Xj на 1% от своей средней  и при фиксированном воздействии на Y других факторов, включенных в уравнение регрессии.
и при фиксированном воздействии на Y других факторов, включенных в уравнение регрессии.
Доверительные интервалы для коэффициентов уравнения регрессии строятся так:
 (20)
(20)
В
|
|
|


