 |
Аналитическое выравнивание временных рядов, оценка параметров уравнения тренда
|
|
|
|
Метод обработки временных рядов, целями которого является устранение случайных колебаний и построение аналитической функции, характеризующей зависимость уровней ряда от времени – тренда, называется аналитическим выравниванием временного ряда.
Суть метода аналитического выравнивания состоит в том, чтобы заменить фактические уровни временного ряда  на теоретические
на теоретические  . Расчет
. Расчет  осуществляется по некоторому формализованному уравнению, принятому за математическую модель тренда. Для построения трендов чаще всего применяют такие функции, как:
осуществляется по некоторому формализованному уравнению, принятому за математическую модель тренда. Для построения трендов чаще всего применяют такие функции, как:
· линейная:  ;
;
· степенная:  ;
;
· гиперболическая:  ;
;
· экспоненциальная:  ;
;
· полиномы второго и более высоких порядков:  .
.
Расчет параметров тренда производится методом МНК. В качестве зависимой переменной выступают фактические уровни ряда  , а независимой переменной является время
, а независимой переменной является время  . Заметим, что для нелинейных трендов необходима процедура линеаризации, аналогичная рассмотренной в разделе 3.
. Заметим, что для нелинейных трендов необходима процедура линеаризации, аналогичная рассмотренной в разделе 3.
Выбор функции тренда может быть осуществлен несколькими способами. Наиболее простым считается тот, в ходе которого анализируют цепные абсолютные приросты (первые разности уровней ряда)  , абсолютные ускорения уровней ряда (вторые разности ряда)
, абсолютные ускорения уровней ряда (вторые разности ряда)  и цепные коэффициенты роста
и цепные коэффициенты роста  .
.
Если примерно одинаковы  , то ряд имеет линейный тренд, если же примерно постоянны
, то ряд имеет линейный тренд, если же примерно постоянны  , то для описания тенденции временного ряда следует выбрать параболу второго порядка, и, если примерно равны
, то для описания тенденции временного ряда следует выбрать параболу второго порядка, и, если примерно равны  , необходимо использовать экспоненциальную или степенную функции.
, необходимо использовать экспоненциальную или степенную функции.
Пример 1. 9 Рассчитаем параметры уравнения тренда по следующим данным:
Таблица 5.2
Темпы роста номинальной месячной заработной платы (за 10 месяцев 1999г., % к уровню декабря 1998г.)
|
|
|
| Месяц | Темп роста номинальной заработной платы | Месяц | Темп роста номинальной заработной платы |
| Январь | 82,9 | Июнь | 121,6 |
| Февраль | 87,3 | Июль | 118,6 |
| Март | 99,4 | Август | 114,1 |
| Апрель | 104,8 | Сентябрь | 123,0 |
| Май | 107,2 | Октябрь | 127,3 |
Для выявления тенденции временного ряда рассчитаем цепные абсолютные приросты (первые разности уровней ряда)  , абсолютные ускорения уровней ряда (вторые разности ряда)
, абсолютные ускорения уровней ряда (вторые разности ряда)  и цепные коэффициенты роста
и цепные коэффициенты роста  .
.
Таблица 5.3
| Месяц | t | 
| 
| 
| 
|
| Январь | 82,9 | - | - | - | |
| Февраль | 87,3 | 4,4 | - | 1,053 | |
| Март | 99,4 | 12,1 | 7,7 | 1,139 | |
| Апрель | 104,8 | 5,4 | -6,7 | 1,054 | |
| Май | 107,2 | 2,4 | -3,0 | 1,023 | |
| Июнь | 121,6 | 14,4 | 12,0 | 1,134 | |
| Июль | 118,6 | -3,0 | -17,4 | 0,975 | |
| Август | 114,1 | -4,5 | -1,5 | 0,962 | |
| Сентябрь | 123,0 | 8,9 | 13,4 | 1,078 | |
| Октябрь | 127,3 | 3,7 | -5,2 | 1,035 |
Наибольшей стабильностью отличаются цепные коэффициенты роста. Для описания тенденции временного ряда используем степенной или экспоненциальный тренд. Для того чтобы убедиться в этом, рассчитаем уравнение тренда и коэффициенты детерминации уравнения для наиболее часто применяемых функций, применяя МНК. Получим табл. 5.4. Коэффициенты детерминации рассчитаны по линеаризованным уравнениям регрессии.
Как мы и предполагали, степенной тренд лучше всего описывает тенденцию анализируемого временного ряда, что подтверждается высоким значением коэффициента детерминации. Ñ
Таблица 5.4
Уравнения трендов
| Тип тренда | Уравнение | 
|
| Линейный | 
| 0,873 |
| Парабола второго порядка | 
| 0,920 |
| Степенной | 
| 0,931 |
| Экспоненциальный | 
| 0,856 |
| Гиперболический | 
| 0,728 |
Интерпретация параметров тренда существенно зависит от его типа.
Если тренд имеет линейную форму, то a - начальный уровень временного ряда в период времени t =0 и b - средний за период абсолютный прирост уровней ряда.
Если же ряд имеет, например, экспоненциальный тренд, то a - начальный уровень временного ряда в период времени t =0 и  - средний за единицу времени коэффициент роста уровней ряда.
- средний за единицу времени коэффициент роста уровней ряда.
|
|
|
Трактовка параметров степенного тренда аналогична трактовке параметров экспоненциального тренда.
Пример (продолжение примера 1). Согласно уравнению линейного тренда  темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 82,66% со средним за месяц абсолютным приростом в 4,72 процентных пункта.
темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 82,66% со средним за месяц абсолютным приростом в 4,72 процентных пункта.
Мы можем заменить фактические уровни временного ряда  на теоретические
на теоретические  , подставляя значения t в уравнение тренда:
, подставляя значения t в уравнение тренда:

Уравнение экспоненциального тренда в исходной форме имеет вид:
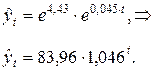
Таким образом, начальный уровень ряда в начальный период времени равен 83,96, а средний цепной коэффициент роста - 1,045. Следовательно, темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 83,96% со средним за месяц цепным коэффициентом роста в 104,5%. Теоретические значения временного ряда рассчитываются как:

Уравнение тренда параболы второго порядка имеет вид:
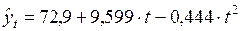 .
.
Следовательно, темпы роста заработной платы за 10 месяцев 1999 г. изменялись от начального уровня 72,9% со среднемесячным абсолютным приростом, описываемым зависимостью вида  . Теоретические значения уровней ряда могут быть рассчитаны как:
. Теоретические значения уровней ряда могут быть рассчитаны как:
 Ñ
Ñ
|
|
|


