 |
Лабораторная работа 2. Экспертная система с использованием ненадежных знаний.
|
|
|
|
Цель: Освоить технологию разработки экспертных систем, приобрести опыт использования коэффициентов доверия и байесовских правил при решении задач.
Методика выполнения
Для выполнения работы необходимо выполнить следующее:
1) составить и ввести базу знаний:
a) выбрать предметную область (ПО);
b) определить цели в выбранной ПО - вопросы на которые должна будет отвечать экспертная система;
c) выбрать тип используемой нечеткой логики, если номер вашей зачетной книжки четный, то используйте логику на основе коэффициентов уверенности и при записи базы знаний задайте коэффициенты уверенности фактов и правил, если нет – логику на основе вероятностей. Необходимые вероятности будут запрошены у пользователя в ходе работы программы;
d) записать правила и факты, позволяющие экспертной системе отвечать на определенные вопросы;
ПРЕДСТАВЛЕНИЕ ЗНАНИЙ ПРАВИЛАМИ И ВЫВОД
В настоящее время разработано множество моделей представления знаний, используемых для реализации систем, основанных на знаниях, при чем во всех из них знания представлены с помощью правил (знаний для принятия решений) вида «ЕСЛИ - ТО» (явление - реакция). Систему продукций можно считать наиболее распространенной моделью представления знаний. Рассмотрим базовые структуры систем продукций и изложим различные технические аспекты, касающиеся практической реализации систем, основанных на знаниях.
Основные системы продукций
Продукционная система состоит из трех основных компонентов. Первый из них это набор правил, используемых как база знаний, поэтому его еще называют базой правил. Следующим компонентом является рабочая память, в которой хранятся предпосылки, касающиеся конкретных задач предметной области, и результаты выводов, полученных на их основании, и наконец, следует механизм логического вывода, использующий правила в соответствии с содержимым рабочей памяти.
|
|
|
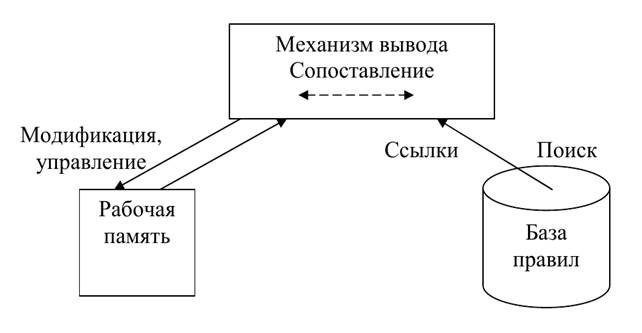
Эти системы бывают двух диаметрально противоположных типов – с прямыми и обратными выводами. Типичным представителем систем первого типа является система MYCIN, используемая для решения задач диагностического характера, а типичным представителем второго типа − OPS, используемая для решения проектирования задач.
В системе продукций обратными выводами с помощью правил строится дерево вывода И-ИЛИ связывающее в единое целое факты и заключения; оценка этого дерева на основании фактов, имеющихся в БД, и есть ло гический вывод. Логические выводы бывают прямыми, обратными и двунаправленными. При прямом выводе отправной точкой служит предоставленные данные, процесс оценки приостанавливается в узлах с отрицанием, при чем в качестве заключения (если все дерево пройдено) используется гипотеза соответствующая самому верхнему уровню дерева (корню). Однако для такого вывода характерно большое количество данных, а также оценок дерева, не имеющих прямого отношения к заключению, что излишне. Преимущество обратных выводов в том, что оцениваются только те части дерева, которые имеют отношение к заключению, однако если отрицание или утверждение невозможны, то порождение дерева лишено смысла. В двунаправленных выводах оценивается сначала небольшой объем полученных данных и выбирается гипотеза (по примеру прямых выводов), а затем запрашиваются данные, необходимые для принятия решения о пригодности данной гипотезы. На основе этих выводов можно реализовать более гибкую и мощную систему.
Системы продукций с прямыми выводами включают три компонента: базу правил, состоящую из набора продукций (правил вывода), базу данных, содержащую множество фактов, и интерпретатор для получения логического вывода на основании этих знаний. База правил и база данных образуют базу знаний, интерпретатор соответствует механизму логического вывода. Вывод выполняется в виде цикла, «понимание-выполнение», причем в каждом цикле выполняемая часть выбранного правила обновляет базу данных. В результате содержимое баз данных преобразуется от первоначального к целевому, т.е. целевая система синтезируется в базе данных. Иначе говоря, для системы продукций характерен простой цикл вы бора и выполнения (или оценки) правил, однако из-за необходимости периодического сопоставления с образцом в базе правил (отождествлением) с увеличением числа последних (правил) существенно замедляется скорость вывода. Следовательно, такие системы не годятся для решения крупномасштабных задач.
|
|
|
Для того чтобы показать, как взаимодействуют компоненты, рассмотрим несложный пример. Допустим, что данные, записываемые в рабочую память, представляют собой образцы в виде набора символов. Например, «намерения – отдых», «место отдыха – горы» и т. д. Правила, накапливаемые в базе правил, отражают содержимое рабочей памяти. В их условной части находятся либо одиночные образцы, либо несколько условий, соединенных предлогом «и», а в заключительной части – образцы, дополнительно регистрируемые в рабочей памяти.
Рассмотрим два примера подобных правил.
Правило 1.
ЕСЛИ «намерение – отдых» и «дорога ухабистая» ТО «использовать джип».
Правило 2.
ЕСЛИ «место отдыха – горы»
ТО «дорога ухабистая».
После того, как в рабочую область памяти записываются образцы «намерение – отдых» и «место отдыха – горы», рассматривается возмож ность применения этих правил.
Сначала механизм вывода сопоставляет образцы из условной части правила с образцами, хранимыми в рабочей памяти. Если все образцы имеются в рабочей памяти, условная часть считается истинной, в противном случае – ложной. В данном примере образец «намерение — отдых» существует в рабочей памяти, а образец «дорога ухабистая» отсутствует, поэтому его условная часть считается ложной. Что касается правила 2, то его условная часть истинна. Поскольку в данном случае существует только одно правило с истинной условной частью, то механизм вывода сразу же выполняет его заключительную часть и образец «дорога ухабистая» зано сится в рабочую память. При попытке вторично применить эти правила получается, что можно применить лишь правило 1, поскольку правило 2 уже было дополнено новым образцом – результатом применения правила 2, поэтому условная часть правила 1 становится истинной, и содержимое рабочей памяти наполняется образцом его заключительной части – «использовать джип». В итоге правил, которые можно было бы применять, не остается, и система останавливается.
|
|
|
В приведенном примере для получения выводе совершалась работа по извлечению предварительно записанного содержимого рабочей памяти, применению правил и дополнения данных, помещаемых в память. Такие выводы называются прямыми. Напротив, способ, при котором на основании фактов, требующих подтверждения, чтобы выступать в роли заключения, исследуется возможность применения правила, пригодного для подтверждения, называется обратным выводом. Чтобы объяснить этот способ, вернемся к нашему примеру. Допустим, что цель – это «использовать джип», и исследуем сначала возможность применения правила 1, подтверждающего этот факт. Поскольку образец «намерение - отдых» из условной части правила 1 уже занесен в рабочую память, то для достижения цели достаточно подтвердить факт «дорога ухабистая». Однако, если принять образец «дорого ухабистая» за новую цель, то потребуется правило, подтверждающее этот факт. Поэтому исследуем возможность применения правила 2.Условная часть этого правила в данный момент является истинной, поэтому правило 2 можно сразу же применять, а рабочая память при этом пополнится образцом «дорога ухабистая», и в результате возможности применения правила 1 подтверждается цель «использовать джип».
В случае обратного вывода условие останова системы очевидны: либо достигается первоначальная цель, либо кончаются правила, применяемые для достижения цели в ходе вывода. Что касается прямого вывода, то как было сказано, отсутствие применимых правил также является условием останова системы. Однако система останавливается и при выполнении некоторого условия, которому удовлетворяет содержимое рабочей памяти, например путем проверки появления образца «использовать джип». В приведенном примере на каждом этапе прямого вывода можно было применять только одно правило, поэтому особых проблем здесь не возникало. В общем случае на каждом этапе вывода таких правил несколько, и тут возникает проблема выбора подходящего из них. Для наглядности дополним этот пример следующим правилом.
|
|
|
Правило 3.
ЕСЛИ «намерение - отдых»
ТО
«нужна скорость»
Кроме того, введем еще одно условие останова системы: появление в рабочей памяти образца «использовать джип». Итак, вследствие добавления нового правила на новом этапе вывода появляется возможность применять правило 2 и правило 3. Если сначала применить правило 2, то на следующем этапе можно будет применить правило 1 и правило 3. Если на этом этапе применить правило 1, то выполняется условие останова системы, но если прежде применить правило 3, то потребуется еще один этап вывода, поэтому выбирают правило 1 и система останавливается. Этот несложный пример показывает, что выбор применяемого правила оказывает прямое влияние на эффективность вывода. В реальной системе, требующей представления множества правил, это очень сложная проблема. Если на каждом этапе логического вывода существует множество применимых правил, то это множество носит название конфликтного набора, а выбор одного из них называется разрешением конфликта. Эта же проблема характерна и для обратных выводов, т. е. когда для достижения одной цели рассматривается применение множества правил, то возникает проблема выбора одного из них. Например, дополним предыдущий пример следующим правилом.
Правило 4.
ЕСЛИ «место отдыха - пляж»
ТО
«дорога ухабистая»
Если на основании этого условия подтверждается цель «использовать джип», то для достижения первоначальной цели достаточно применить только одно правило 1, однако, чтобы подтвердить новую цель «дорога ухабистая», открывающую возможность применения правила 1, нужно выбрать либо правило 2, либо правило 4. Если сначала применим правило 2, то это будет самый удачный выбор, поскольку сразу же можно применить и правило 1. С другой стороны, если попытаться применить правило 2, то поскольку образец «место отдыха - пляж», который является условием правила 4, в рабочей памяти не существует, и кроме того, не существует правила подтверждающего его, данный выбор является неудачным и лишь со второго захода, применяя правило 2, можно подтвердить цель «дорога ухабистая». Обратите внимание на тот факт, что при обратном выводе применения правила 3, которое не оказывает прямого влияния на достижения цели, не принималось в расчет с самого начала. Таким образом, для обратных выводов характерна тенденция исключения из рассмотрения правил, не имеющих прямого отношения к заданной цели, что позволяет повысить эффективность вывода.
|
|
|
До сих пор рассматривалась базовая структура продукционных систем, однако на практике для построения действующих систем необходимы дополнительные средства. Прежде всего в некоторых случаях недостаточно записи в рабочую память лишь одного образца и возникает необходимость управления данными, уточняющими смысл. В таких случаях довольно часто используется способ представления конкретных данных с памятью триплета: объект, атрибут, значение. По этому способу отдельная субстанция из предметной области (человек, предмет и т. п.) рассматривается как один объект, и можно считать, что данные, хранимые в рабочей памяти, показывают значения, которые принимают атрибуты этого объекта. Например, данные (собака 1 кличка шарик) показывает тот факт, что существует (некоторая) собака и кличка этой собаке – Шарик. Одним из преимуществ, связанным с внедрением структуры объект-атрибут-значение, является уточнение контекста, в котором применяется правило. Например, правило, единое для всех объектов «собака», должно быть пригодным для применения независимо от того, идет ли речь о собаке по кличке Шарик или о другой собаке по кличке Жучка.
При умелом использовании структуры данных типа «объект-атрибут-значение» можно повысить эффективность поиска содержимого рабочей памяти. Например, в системе MYCIN объекту соответствует атом (понятие языка Лисп для представления элементарных объектов), атрибуту – имя свойства этого атома, а значению – значение свойства. Представление данных с помощью триплета «объект-атрибут-значение» можно легко расширить для описания данных, включающих показатели нечеткости. Например, в системе MYCIN применяется показатель нечеткости, который называется фактором достоверности (фактором уверенности, коэффициентом уверенности). Таким образом, данные управляются при помощи ассоциативной четверки «объект-атрибут-значение-фактор достоверности». Главным моментом в основых системах продукций является исследование (проверка) наличия специальных данных, касающихся условной части правила, в рабочей памяти. Оценка условной части методом поиска и сопоставления имеет в известном смысле широкую область практического применения, однако в отдельных случаях такая прямая оценка оказывается недостаточной. Рассмотрим, к примеру, случай, когда атрибут некоторого объекта выражается численным значением. Разумеется, и здесь может быть ситуация, когда рассматриваются условия, указывающие, что число принимает определенное значение, однако в большинстве случаев приходится сталкиваться с проблемой сравнения численных значений по величине. Кроме того, могут быть случаи, когда само по себе определение значения атрибута не сопряжено ни с какими трудностями, однако имеется проблема определения принадлежности этого значения к некоторой категории. Для описания подобных условий введено понятие «предикат».
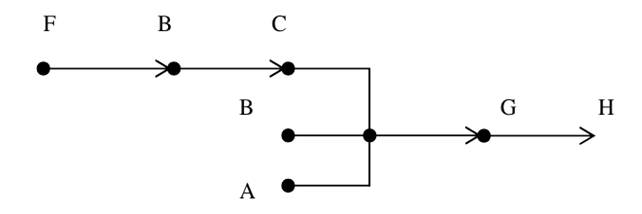
Пример. Рассмотрим упрощенный пример продукционной системы с консеквент-выводимой архитектурой (прямая цепочка вывода), а затем с условно-выводимой архитектурой (обратная цепочка вывода). Буквами здесь обозначены элементы БД и они считаются истинными, если содержаться в ней.
БД: А, F.
Правило 1: A∩B∩C→D
Правило 2: D∩F→G
Правило 3: A∩J→G
Правило 4: B→C
Правило 5: F→B
Правило 6: L→J
Правило 7: G→H
Предположим, что цель состоит в выводе D при прямой цепочке рассуждений. В первую очередь проверяется, находится ли D в БД. Так как в данном случае это не так, то система пытается вывести истинность D, используя правила, которые она может выполнить с данной БД. Машина перебирает правила, но не может выполнить 1, 2, 3, 4 правила, но выполняет 5 и заносит в БД D. При втором проходе не выполняются правила 1, 2, 3, но 4 выполняется и в БД заносится C. При следующем проходе выполняется правило 1 и цель достигнута.
Предположим, что цель состоит в том, чтобы вывести истинность H (при обратной цепочке рассуждений). В первую очередь проверяется, находится ли Н в БД? Так как в данном случае это не так, то система пытается вывести истинность G, так как истинность последнего влечет за собой истинность Н. Снова проверяется БД: в БД нет G, следовательно, организуется поиск правила, содержащего G в правой части.
Таких правил несколько (два или три). В качестве стратегии разрешения конфликта будем считать, что правила упорядочены по приоритету, причем правилу с наименьшим номером соответствует больший приоритет.
В данном случае выбирается правило 2, поэтому целью теперь становится вывести истинность D и F. Для этого достаточно показать, что А – истинно (так как находится в БД), В – истинно (согласно правилу 5), С – истинно (согласно правилу 4). Так как истинность D и F доказана, то из правила 2 следует истинность G, а из истинности G – следует истинность Н (правило 7). Таким образом цель достигнута. Элементы, истинность которых доказана, добавляются в БД. В данном случае это элементы H,G,D,C,B.
Построим цепочку выводов (рассуждений) для данного примера, когда целью является D.

Далее построим цепочку выводов, т.е. что существует ситуация Н.
ПРЕДСТАВЛЕНИЕ И ИСПОЛЬЗОВАНИЕ НЕЧЕТКИХ
ЗНАНИЙ
Ненадежные знания и выводы
В задачах, которые решают интеллектуальные системы, иногда приходится применять ненадежные знания и факты, представить которые двумя значениями – истина или ложь (1 или 0) трудно. Существуют знания, достоверность которых, скажем 0.7. Такую ненадежность в современной физике и технике представляют вероятностью, подчиняющейся законам Байеса (для удобства назовем ее байесовской вероятностью), но в инженерии знаний было бы нелогично иметь дело со степенью надежности, приписанной знаниям изначально, как с байесовской вероятностью (нелогично незнания представлять байесовской информацией).
Поэтому одним из первых был разработан метод использования коэффициентов уверенности для системы MYCIN. Этот метод не имеет теоретического подкрепления, но стал примером обработки ненадежных знаний. Предложен и метод выводов, названный субъективным байесовским методом, который использован в системе PROSPECTOP. Позже была введена теория вероятностей Демпстера-Шафера, которая имеет все признаки математической теории. По сравнению с байесовской вероятностью теория Демпстера-Шафера отличается тем, что она не фиксирует значения вероятности, а может представлять и незнания.
Связь между подзадачами, на которые разбита задача, оперирующая двумя понятиями – истина и ложь, может быть представлена через операции И и ИЛИ. В задачах с ненадежными исходными данными кроме И и ИЛИ важную роль играет комбинированная связь, которую будем обозначать КОМБ. Такая связь независимо подкрепляет или опровергает цель на основании двух или более доказательств. Нечеткая логика, ведущая свое происхождение от теории нечетких множеств – это разновидность непрерывной логики, в которой логические формулы оперируют со значениями между 0 и 1. Упомянутые выше методы, продолжающие развитие теории вероятности, несколько отличаются от нечеткой логики, более субъективны, но по своей логической сущности более сильны. Вообще говоря, логика играет важную роль при рассмотрении фундаментальных понятий представления знаний.
Для решения сложных задач можно использовать метод разбиения их на несколько подзадач. Каждая подзадача в свою очередь разбивается на простые подзадачи, поэтому задача в целом описывается иерархически. Знания, которые по условиям подзадач определяют условия задач высшего уровня, накапливаются фрагментарно. В задачах с ненадежными данными знания могут не только иметь степень надежности, равную 1, но и значения между истиной и ложью. Как отмечено выше, при разбиении на подзадачи возможно соединение И, ИЛИ, и КОМБ (комбинированная связь).
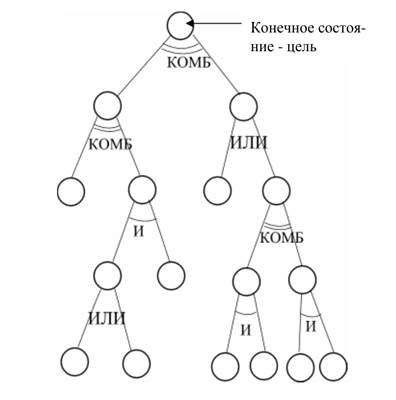
На основании двух и более доказательств цели(или подцели) независимо подтверждаются или опровергаются (в случае противоречивых доказательств), если связь комбинированная. Например, рассмотрим случай определения (диагностирования), простужен ли больной. Пусть доказательство 1 – кашель у больного – надежно со степенью 0.6, а доказательство 2 – температура 39-40 – надежно со степенью только 0.5. Простудное состояние при наблюдении только одного из доказательств простуды можно подтвердить с надежностью 0.6 или 0.5. Но если рассмотреть оба доказательства, то естественно, нужно считать, что простуда куда более достоверна. Если выполнить операцию КОМБ, то мы должны получить, скажем, надежность 0.8. И наоборот, пусть доказательство 1 – наличие кашля – снова имеет надежность 0.6, но температура как доказательство 2 нормальная, тогда при операции комбинированной связи надежность диагноза простуды уменьшится и будет равно, например, 0.45.
Методы представления знаний, конечно, неоднозначны, но метод выводов, приведенный здесь, краток и ясен, поэтому знания будем описывать на основе представления знаний с помощью правил так, как в системе продукций. Способ записи правил, включающих также и комбинированную связь, можно выбрать любой, но сейчас продолжим обсуждение, используя запись, указанную на рисунке, где X,Y – результаты доказательств, А – цель или гипотеза, а И, ИЛИ, КОМБ – виды связей. C1, C2, C31, C32 — это степени надежности, приписанные правилам (знаниям).

Правило: ЕСЛИ X иY, то А с C1.
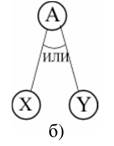
Правило: ЕСЛИ Х или Y, то А с C2 (если Х и Y не могут выполняться одновременно, то правило можно записать в виде двух отедльных правил:
Правило: Если Х, то А с C21
Правило: Если Y, то А с C22)

Правило 1: Если Х, то А с C31
Правило 2: Если Y. То А с C 32
Допустим, что для нашей задачи уже определены степени надежности X и Y как результатов предыдущих выводов или наблюдений, и сделаем вывод или вычислим степень надежности А, используя правила из базы знаний. Кроме общеизвестных методов выбора минимального значения степеней надежности из нескольких выводов при связи И и максимального при связи ИЛИ других подходящих методов не существует, а при связи КОМБ предложен метод MYCIN, рассмотренный ниже, субъективный байесовский метод, а также теория Демпстера-Шафера.
Если выбрать метод выводов как для связи И, ИЛИ, так и для связи КОМБ, то степени надежности можно распространить и на иерархическую сеть выводов. В итоге можно получить степень надежности конечной цели, а также указать ее при окончательном ответе.
В системе MYCIN (известной ЭС по идентификации микроорганизмов в крови) имеют дело с ненадежностью, представленной так называемыми коэффициентом уверенности CF. Этот коэффициент принимает значения в отрезке [-1, 1] (1 – заведомо истинно, -1 – заведомо ложно). Коэффициент уверенности CF[A,X] вывода А, если удовлетворяется предпосылка Х, определим следующим образом, взяв за образец байесовскую вероятность (именно образец, поскольку проводить какую-либо аналогию между CF и вероятностью неправомерно):

Здесь Р(А), Р(А|X) соответственно априорная и апостериорная вероятности. При этом C1, C2, C31, C 32 в правилах будут иметь соответственно вид CF[A,X, и Y], CF[A,X, или Y], CF[A,X], CF[A,Y] и в общем случае называются CF правила.
При выводе прежде всего получают CF предпосылки. Если в предпосылке только один член, то CF уже полученного доказательства и есть CF предпосылки, но при связях И, ИЛИ, CF[X,*], CF[Y,*] доказательств X, Y (* определяется в зависимости от вывода и добавляется для представления так называемого коэффициента уверенности при некотором условии) оп-
ределяется соответственно как минимум и максимум, таким образом CF предпосылки задается следующими формулами.
1. При связи И
CF предпосылки=CF[X и Y, *]=min{CF[X, *], CF[Y, *]}
2. При связи ИЛИ
CF предпосылки=CF[X или Y, *]=max{CF[X, *], CF[Y, *]}
Если CF предпосылки отрицателен, то действие в выводе правила не выполняется, выполняется оно только, если этот коэффициент положителен, т.е. предпосылка удовлетворяется (может быть частично).
При этом вывод достоверен с коэффициентом CF правила* CF предпосылки, и это значение переносится на вывод А:
CF[A,*]=CFправило*CFпредпосылки
А именно, если CFпредпосылки равен 1, то CF вывода А данного правила равен CFправила, но если предпосылка удовлетворяется лишь частично, то CF вывода пропорционально уменьшается.
Итак, при связи КОМБ отдельно получают CF[A, X] и CF[A, Y]. В системе MYCIN действует следующая комбинированная функция:

Коэффициент уверенности CF, полученный из трех и более независимых доказательств, можно вывести, последовательно используя указанные выше формулы, но при получении положительных и отрицательных CF прежде всего следует уточнить, какой знак имеют CF в формулах
CF [ A, X ] + CF [ A, Y ] − CF [ A, X ] CF[ A, Y ],
если CF [ A, X ] > 0 и CF[ A, Y ] > 0,
и,
CF [ A, X ] + CF [ A, Y ] + CF [ A, X ]CF[ A, Y ],
если CF [ A, X ] < 0 и CF [ A, Y ] < 0
а уже затем применить формулу
CF [ A, X ] + CF [ A, Y ],
если CF [ A, X ] CF [ A, Y ] ≤ 0, (*)
СF [ A, X ] = ±1 и CF[ A, Y ] = ±1
для разнознаковых CF.
Если не придерживаться этого порядка, то в зависимости от порядка формул будут получаться различные CF. В системе MYCIN положительные CF называют мерой доверия, а отрицательные CF = мерой недоверия. Различие результата расчета CF при изменении порядка применения формул неудобно, поэтому в системе EMYCIN (универсальной ЭС, созданной на базе MYCIN) формула (*) преобразована в следующую формулу:

В системе MYCIN применяется вывод, направляемый целью (вывод сверху-вниз), но если абсолютное значение CF подцели меньше порогового значение 0.2, то соответствующие правила для вывода не используются, а информация считается недостоверной. Коэффициенты уверенности в системе MYCIN не имеют под собой строгого фундамента, но благодаря простоте восприятия они нашли широкое применение во многих универсальных средствах обработки знаний.
Поскольку эвристические правила ЕСЛИ-ТО основываются исключительно на человеческом опыте, с полной определенностью никогда нельзя сказать, что они верны. Пользователь интеллектуальной системы также не может быть полностью уверен, что значения, которые он приписывает переменным, абсолютно корректны. Например, правило:
ЕСЛИ Процентные ставки=падают и налоги уменьшаются,
ТО уровень цен на бирже=РАСТЕТ
верно не всегда, поэтому можно приписать ему значение некоторого коэффициента уверенности CF (или КУ).
Пусть приведенное правило имеет CF, равный 0.9 и нельзя утверждать, что процентные ставки падают, т.е. первому условию правила назначен CF, равной 0.6. Кроме того, допустим, что налоги колеблются), то увеличиваются, то уменьшаются), поэтому предположить уменьшение налогов можно, только если КУ равен 0.8. Тогда правило можно записать так:
ЕСЛИ Процентные ставки=падают (КУ=0.6) И
Налоги уменьшаются (КУ=0.8),
ТО уровень цен на бирже=РАСТЕТ (КУправила=0.9).
Коэффициент уверенности, что уровень цен на бирже будет расти может быть подсчитан следующим образом: выбирается минимальный КУ для условной части ЕСЛИ правила, разделенных логическим оператором И, и умножается на КУ для всего правила. Для приведенного примера:
(minimum(0.6; 0.8))*0.9=0.6*0.9=0.54
Следовательно при КУ=0.54 можно сказать, что уровень цен на бирже будет падать. Если есть еще одно правило с тем же логическим выводом о росте уровня цен на бирже, но другим наборам условий, то КУ для этого вывода нужно выбрать максимальным из КУ для вывода первого правила и КУ для вывода второго правила. На первый взгляд все это кажется очень сложным, поэтому разберем пример.
Прежде всего сформулируем общие принципы.
1. Выбрать максимальное значение КУ из КУ для условий правила, разделенных логическим оператором И.
2. Если в правиле есть оператор ИЛИ, выбрать максимальное значение из КУ для всех условий правила, разделенных оператором И для всех условий, связанных оператором ИЛИ.
3. Умножить выбранный КУ на КУ правила.
4. Если существует несколько правил с одинаковым логическим выводом, выбрать из всех полученных КУ максимальный.
Пример. Рассмотрим два правила с одним и тем же логическим выводом С:
ЕСЛИ А(КУ=0.3) И В(КУ=0.6),
ТО С(КУ=0.5)
ЕСЛИ D(КУ=0.4) И Е(КУ=0.7),
ТО С(КУ=0.9).
В приведенных правилах КУ для логического вывода С подсчитывается следующим образом:
Maximum(minimum (0.3; 0.6)*0.5), minimum (0.4;0.7)*0.9=
= maximum((0.3*0.5), 0.4*0.9))=maximum(0.15;0.36)=0.36.
Возьмем пример с использованием логического оператора ИЛИ:
ЕСЛИ А(КУ=0.3) И В(КУ=0.6) ИЛИ D(КУ=0.5), ТО С(КУ=0.4).
В этом примере КУ для логического вывода С считается так:
Maхimum(minimum(0.3;0.6);0.5)*0.4=maximum(0.3;0.5)*0.4=0.5*0.4=0.2
|
|
|


