Лабораторная работа №3. Экспертная система с использованием нечетких множеств.

 

Цель: Освоить технологию разработки экспертных систем, приобрести опыт использования нечетких множеств и правил нечеткого вывода.

Методика выполнения

Для выполнения работы необходимо выполнить следующее:

1) составить и ввести базу знаний:

a) выбрать предметную область (ПО);

b) определить цели в выбранной ПО - вопросы на которые должна будет отвечать экспертная система;

c) выбрать тип используемой нечеткой логики;

d) записать правила и факты, позволяющие экспертной системе отвечать на определенные вопросы;

 

Нечеткие множества

 

Знания не всегда могут быть описаны точно – часто встречаются так называемые «нечеткие знания». Люди повседневно решают проблемы и делают заключения в среде «нечетких знаний», а для того чтобы интеллектуальные системы обладали такими возможностями как гибкость, широкий кругозор, адаптируемость, необходимо представление и использование нечетких знаний. Все нечеткости, с которыми имеет дело инженерия знаний, можно классифицировать следующим образом:

1) недетерминированность выводов;

2) неоднозначность (зашумленный сигнал);

3) ненадежность (в силу ограниченности точности прибора);

4) неполнота (пропуск значений в таблице факторы/испытания);

5) собственно нечеткость (лингвистические аспекты языка).

Методологической основой для формализации нечетких знаний является теория нечетких множеств.

Когда мы говорим «Старик», то неясно, что мы имеем в виду:

старше 50, старше 60 или старше 70? Одним из методов изучения множеств без уточнения их границ является теория нечетких множеств, которая была предложена Л. Заде в 1965 г. и продолжает развиваться. Эти исследования связаны также с нечеткими выводами, которые выполняются с использованием правил, представленных как нечеткие множества. В данном разделе мы ознакомимся с основными понятиями теории нечетких множеств и методами нечетких выводов.

Определение

Нечеткое подмножество F множества элементов U определяется функцией принадлежности μ_F(u). Эта функция отображает элементы u множества U на множество чисел в интервале [0,1], которые указывают степень принадлежности каждого элемента нечеткому подмножеству F.

Если множество U состоит из конечного числа элементов { u₁, u₂,..., u_n }, то нечеткое подмножество F можно представить следующим образом:

 

F = μ_F(u₁) / u₁ + μ_F(u₂) / u₂ +... + μ_F(u_n) / u_n = ∑ μ_F(u_i) / u_i.

 

Следует иметь в виду, что знак плюс в этой формуле означает не суммирование, а объединение или конъюнкцию, а символ «/» показывает, что значение μ_A(u_i) относится к элементу, следующему за ним.

Пример

U = 1 + 2 + 3 +... + 10. Тогда нечеткое множество А, которое описывается понятием «несколько», можно записать в следующем виде:

«несколько» = 0,4/2 + 0,7/3 + 0,8/9, символ «=» означает здесь равенство по определению.

В случае непрерывного множества U вводится следующее обозначение подмножества

F: ∫ μ (u) / u.

 

Следует иметь в виду, что знак ∫ в приведенной выше формуле означает не интегрирование, а объединение. Заметим также, что если μ A (u) принимает значение только 0 или 1, то множество А является обычным множеством. Запись μ_A(u) = 1 означает, что элемент u Є U принадлежит множеству А, т.е. u Є A. Запись μ_A(u) = 0 означает, что u Є U не принадлежит множеству А, т.е. u 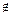U.

Пусть U – множество людей в возрасте 0–100 лет, функции принадлежности нечетких множеств, означающих возраст: «Молодой», «Средний», «Старый» можно определить при помощи графика.

 

 

 

При дискретизации через 10 лет получим приблизительно следующее:

молодой = 1/0 + 1/10 + 0,9/20 + 0,3/30,

средний = 0,8/30 + 1/40 + 0,8/50,

старый = 0,3/50 + 0,9/60 + 1/70 + 1/80 + 1/90+ 1/100.

Здесь элементы множества с функцией принадлежности, равной 0, не записываются.

 

Операции на нечетких множествах

 

Над нечеткими множествами выполняются те же операции, что и над обычными множествами. Понятие нечеткого подмножества Л. Заде определил следующим образом: нечеткое подмножество данного конечного множества U – это такое подмножество, значения степеней принадлежности элементов которого лежат в единичном интервале [0,1]. Пусть A = ∫ μ_A(u) / u

и B = ∫ μ_B (u) / u − два нечетких множества, тогда нечеткое множество A является подмножеством нечеткого множество B (A 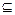B), если для всех u справедливо неравенство μ_A(u) ≤ μ_B(u).

Равенство двух нечетких множеств определяется следующим образом: два нечетких множества A и B равны (A = B), если для всех u справедливо μ_A(u) = μ_B(u).

ОБЪЕДИНЕНИЕ нечетких множеств А и В:

A U B = ∫ (μ_A(u) ∨ μ_B (u)) / u,

где

(μ_A(u) ∨ μ_B(u)) = max(μ_A(u), μ_B (u)).

 

ПЕРЕСЕЧЕНИЕ нечетких множеств А и В:

A ∩ B = ∫ (μ_A(u) ∧ μ_B (u)) / u,

где

(μ_A(u) ∧ μ_B(u)) = min(μ_A(u), μ_B (u)).

ДОПОЛНЕНИЕ или ОТРИЦАНИЕ определяется следующей

формулой: ~ A = ∫ (1 − μ_A(u)) / u.

 

Квантификатор не может интерпретироваться с помощью операции отрицания:

не x = (1 − μ_x(u)) / u.

РАЗНОСТЬ двух нечетких множеств определяется формулой

A − B = A∩ ~ B.

ДИЗЪЮНКТИВНАЯ СУММА определяется соотношением

A + B = (A ∪ B) − (A ∩ B).

Например,

~(молодой) = 0,1/20+0,7/30+1/40+1/50+1/60+1/70+1/80+1/90+1/100.

(молодой) ∪ (средний) = 1/0+1/10+0,9/20+0,8/30+1/40+0,8/50.

(молодой) ∩ (средний) = 0,3/30.

 

ПРОИЗВЕДЕНИЕ нечетких множеств А и В определяется следующим соотношением:

A · B = ∫ (μ_A(u) · μ_B(u)) / u.

 

Операция возведения в степень

A^b = ∫ (μ_A(u))^b / u, где b > 0.

Операция концентрирования нечеткого множества

CON(A) = A².

Эта операция уменьшает степень принадлежности элементов тем больше, чем меньше степень их принадлежности первоначальному множеству А. Квантификатор очень может интерпретироваться с помощью операции концентрации, то есть возведения в квадрат:

очень x = ∫ μ_x²(u) / u.

Операция растяжения нечеткого множества является противоположной концентрации и определяется соотношением DIL(A) = A^0,5.

Операция контрастной интенсивности определяется соотношением

 

Эта операция увеличивает значения μ_A(u), которые больше 0,5, и уменьшает те значения μ_A(u), которые меньше 0,5, уменьшая тем самым нечеткость А.

 

Нечеткие отношения

Пусть U и V – универсальные множества, на которых определены X и Y соответственно, тогда нечеткое отношение R: X → Y определяется как подмножество декартова произведения двух нечетких множеств X ×Y ⊆ U × V, которое задается с помощью функции принадлежности двух переменных по формуле R = ∫ μ_R(u, v) /(u, v) (X ×Y).

 

В общем случае n-арное отношение, или n-отношение, определяется следующим образом. Пусть R – результирующее множество декартова произведения n множеств и μ – его функция принадлежности.

Нечеткое n-отношение определяется как нечеткое подмножество R, принимающее какое-либо значение на интервале функции принадлежности в соответствии со следующей формулой:

R = ∫ μ_R(u₁,..., u_n) / (u₁,..., u_n).

(X₁ ×... × X_n)

x_i ∈ X_i, i = 1,..., n.

Пример

Допустим, что Х = {Иван, Марья};

Y = {Петр, Дарья}, тогда

Дружба = 0.6/(Иван, Петр) + 0.9/(Иван, Дарья) + 0.8/(Марья, Петр) + 0.1/(Марья, Дарья).

Отношения удобно записывать с помощью матрицы отношений

	Петр	Дарья
Иван	0.6	0.9
Марья	0.8	0.1

 

Допустим, что существует нечеткое знание-правило типа если F, то G (если старый, то умный), использующее нечеткие множества F ⊂ U и G ⊂ V. Тогда один из способов построения нечеткого отношения из соответствующей области полного множества U в область полного множества V состоит в следующем:

R = F × G = ∫ (μ_F(u) ∧ μ_G(v)) /(u, v) (U ×V)

или

R = F × G = ∑ ∑ (μ_F(u_i) ∧ μ_G(v_j)) / (u_i, v_j).

 

Необходимо отметить, что есть и другие способы построения нечеткого отношения.

Пусть U и V – это области натуральных чисел от 1 до 4, тогда определим следующим образом нечеткие множества:

F = маленькие = 1/1 + 0.6/2 + 0.3/3 + 0/4,

G = большие = 0/1 + 0.1/2 + 0.6/3 + 1/4.

Если есть нечеткое знание-правило если u – маленькое, то v – большое, то можно следующим образом построить нечеткое отношение, определяющее данное знание -правило:

 

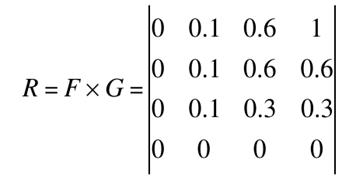
Пусть R – нечеткое отношение из области U в область V, S – нечеткое отношение из области V в область W, тогда нечеткое отношение из области U в область W определяется как свертка max-min:

 

 

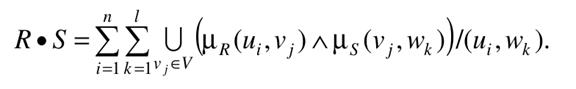
Здесь знак «•» обозначает свертку max-min,

∪ – взятие максимума для всех v_j;

∧ – взятие минимума.

Пример

U = V = W = {1, 2, 3, 4}.

F = маленькие = 1/1 + 0.6/2 + 0.3/3 + 0/4,

G = большие = 0/1 + 0.1/2 + 0.6/3 + 1/4.

~F = не_ маленькие = 0/1 + 0.4/2 + 0.7/3 + 1/4,

G 2 = очень_большие = 0/1 + 0.01/2 + 0.36/3 + 1/4 или, округлив, 0/1 + 0 /2 + 0.4/3 + 1/4. Тогда если есть знание-правило если v – не маленькое, то w – очень большое, то в соответствии с формулой S = ~F × G 2 можно построить нечеткое отношение S из V в W

 

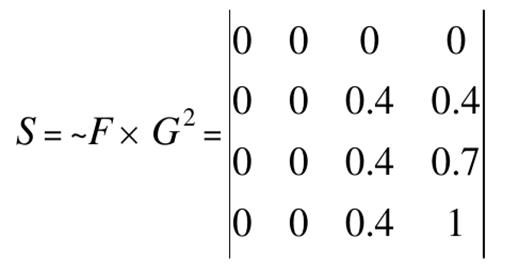
И далее можно построить нечеткое отношение из U в W.

 

 

Вывод на нечетких знаниях

Традиционный дедуктивный вывод, называемый также модус поненс, записывается следующим образом:

P ⇒ Q

P

______

Q

Что означает вывод Q из факта P по правилу P ⇒ Q.

Используя те же обозначения, можно определить нечеткий дедуктивный вывод следующим образом:

P ⇒ Q

P′

______

Q′

Однако эта формулировка имеет существенное отличие от традиционного модус поненс. Здесь не требуется совпадения высказывания P′ в факте и высказывания P в правиле. В общем случае могут не совпадать и заключения Q и Q′.

Л. Заде предложил нечеткий условный вывод в следующей форме:

если х есть А, то y есть В, иначе y есть С

х есть А'

___________________________________

y есть D

Здесь x, y – имена объектов; A, A ', B, C, D – нечеткие понятия, представленные нечеткими множествами, определенными на U, U, V, V, V соответственно.

Предложено несколько правил, переводящих нечеткое условное высказывание «если х есть А, то y есть В, иначе y есть С» в нечеткое отношение U • V.

Пусть А, В, С – нечеткие множества в U, V, V, заданные в виде A = ∫ μ_A(u) / u; B = ∫ μ_B(v) / v; C = ∫ μ_C(v) / v.

 

Тогда имеем:

А. Максиминное правило Rm':

Rm′ = (A × B) ∪ (~ A × C) = ∫ (μ_A(u) ∧ μ_B(v)) ∨ (1 − μ_A(u)) ∧ μ_C(v) /(u, v).

 

Б. Арифметическое правило Ra':

Ra ′ = (~ A × V + U × B) ∩ (A × V + U × C) =

∫ 1 ∧ (1 − μ_A(u) + μ_B(v)) ∧ ((μ_A(u) + μ_C(v)) /(u, v).

 

В. Размытое бинарное правило

Rb′ = (~ A × V ∪ U × B) ∩ (A × V ∪ U × C) =

= ∫ 1 ∧ (1 − μ_A(u) ∨ μ_B(v)) ∧ ((μ_A(u) ∨ μ_C(v)) /(u, v).

 

Г. Правила Танака-Мидзумото

гделенькоеRg g ′ = (~ A × V ⇒ U × B) ∩ (A × V ⇒ U × C) =

= ∫ 1 ∧ (μ A (u) → μB(v)) ∧ ((1 − μ A(u) → μ A (v)) /(u, v),

 

(1, если μ_A ≤ μ_B;

μ_A(u) → μ_A(v) = (

(μ_B, если μ_A ≥ μ_B.

Таким образом, возвращаясь к исходной постановке задачи:

если х есть А, то y есть В, иначе y есть С

х есть А'

__________________________________________

y есть D,

следствие D можно вывести следующим образом:

Dm = А' • Rm',

Da = А' • Ra',

Db = А' • Rb',

Dgg = А' • Rgg'.

Пусть имеются следующие посылки:

x – не очень маленькое;

если x – маленькое, то y – большое, иначе y – маленькое.

Найти значения y’. Множество U = 1 + 2 + 3.

маленькое = 1/1+ 0.4/2;

большое = 0.5/2+ 1/3.

Тогда термин очень маленькое = 1/1+ 0.16/2, а не очень маленькое

= 0.84/2+ 1/3.

Отношение для максиминного правила:

Rm ′ = (A × B) ∪ (~ A × C) = ∫ (μ_A(u) ∧ μ_B(v)) ∨ (1 − μ_A(u)) ∧ μ_C(v) /(u, v).

 

Здесь A = маленькое, B = большое, C = маленькое.

Пример вычисления значений элементов матрицы Rm ' приведен ниже:

(u 1, v 1) = (1 ∧ 0) ∨ (0 ∧ 1) = 0; (u2, v 1) = (0.4 ∧ 0) ∨ (0.6 ∧ 1) = 0.6;

(u 1, v2) = (1 ∧ 0.5) ∨ (0 ∧ 0.4) = 0.5; (u2, v2) = (0.4 ∧ 0.5) ∨ (0.6 ∧ 0.4) = 0.4;

(u 1, v 3) = (1 ∧ 1) ∨ (0 ∧ 0) = 1;

(u 2, v3) = (0.4 ∧ 1) ∨ (0.6 ∧ 0) = 0.4;

(u3, v 1) = (0 ∧ 0) ∨ (1 ∧ 1) = 1;

(u3, v2) = (0 ∧ 0.5) ∨ (1 ∧ 0.4) = 0.4;

(u3, v 3) = (0 ∧ 1) ∨ (1 ∧ 0) = 0.

 

 

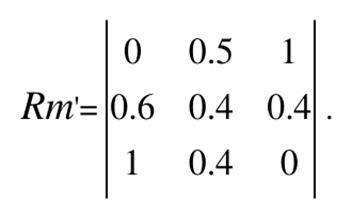
Тогда значение y’ может быть определено следующим образом

y’ = не очень маленькое • Rm' =

 

т.е. y’ = 1/1+ 0.4/ 2 + 0.4/3, что может быть интерпретировано (с некоторой натяжкой) как довольно-таки маленькое.

Далее рассмотрим для указанных выше посылок арифметическое правило Ra':

Ra′ = (~ A × V + U × B) ∩ (A × V + U × C) =

∫ 1 ∧ (1 − μA(u) + μB(v)) ∧ ((μA(u) + μC (v)) /(u, v) =

 

 

Тогда значение y’, используя арифметическое правило, может быть определено следующим образом:

y’ = не очень маленькое • Ra' =

 

т.е. y’ = 1/1+ 0.8/2 + 0.4/3.

Вывод с использованием размытого бинарного правила приведен ниже:

Rb′ = (~ A × V ∪ U × B) ∩ (A × V ∪ U × C) =

= ∫ 1 ∧ (1 − μA (u) ∨ μB (v)) ∧ ((μA(u) ∨ μC (v)) /(u, v) =

Тогда значение y’, может быть определено следующим образом:

y’ = не очень маленькое • Rb' =

т.е. y’ = 1/1+ 0.4/2 + 0.4 /3, что может быть также интерпретировано как довольно-таки маленькое.

Последний нечеткий вывод проведем с использованием правила Танака- Мидзумото

Rgg'= (A × V ⇒ U × B) ∩ (~A × V ⇒ U × C) = ∫ (μA(u) → μB(v)) ∧ ((1 − μA(u) → μC(v))/(u, v)

 

(1, если μ_A ≤μ_B;

μ_a(u) → μ_b(v) = (

(μ_B, если μ_A >μ_B;

 

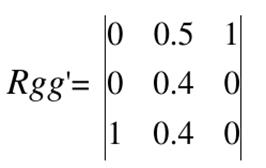
y’ = не очень маленькое • Rgg ' =

 

 

т.е. y’ = 1/1+ 0.4/2 + 0/3, что интерпретируется как маленькое.

Рассмотренные примеры показывают, что использование отношений Rm ', Ra', Rb' для нечеткого вывода не дают следствий, которые совпадали бы с нашими интуитивными представлениями. Лучшие результаты дает отношение Rgg'.

В классической логике известно и еще одно правило вывода, носящее имя модус толленс. Записывается оно следующим образом:

P → Q

~Q

–––

~P

 

 

В нечетком выводе на основе правила модус толленс импликация должна удовлетворять закону контрапозиции, т.е. P → Q = ~Q → ~P.

Это необходимо для обеспечения эквивалентности правил «если х есть А, то y есть В» и «если y есть не В, то х есть не А».

 

 

 

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: