Основные физические свойства воздуха

Глава I. ОСНОВЫ АЭРОДИНАМИКИ КРЫЛА

Основные параметры воздуха

В состоянии неподвижности воздух характеризуется следующими параметрами: давление (Р), температура (Т) и плотность (ρ).

Давление — сила, перпендикулярно действующая на единицу поверхности. За единицу давления принято дав­ление, равное одному килограмму на один квадратный сантиметр (кг/см²), эта величина называется техниче­ской атмосферой.

Давление, вызываемое массой вышележащих слоев воздуха, называется атмосферным давлением и обычно измеряется в миллиметрах ртутного столба. Давление в 1 кг/см² уравновешивается столбом ртути высотой в

735,6 мм

где β— атмосферное давление, мм рт. ст.

Температура характеризует скорость хаотического движения молекул; чем больше температура, тем быст­рее движутся молекулы, и наоборот.

Измерение температуры производится по шкале Цельсия и Кельвина. За 0° по шкале Цельсия принята температура таяния льда, а за 100° — температура ки-

 

пения воды при давлении 760 мм рт. ст. За 0° по шкале Кельвина принята температура —273° С. При этой тем­пературе прекращается движение молекул газа.

Температура в градусах Цельсия обозначается —

t С, а в градусах Кельвина — Т° К:

Плотность воздуха -это масса, заключенная в еди­нице объема. Она определяется по формуле

где m — масса, кг; V — объем, м³.

Все эти параметры воздуха связаны между собой уравнением состояния газа. Для воздуха, средний мо­лекулярный вес которого (М) равен 29, уравнение име­ет такой вид:

где Р — давление, кг/м²; ρ — массовая плотность воз­духа, кг•с²/м⁴.

Из уравнения состояния газа вытекают, как частные случаи, известные законы Бойля—Мариотта и Гей-Люс-сака, открытые в свое время опытным путем. Так, при неизменной температуре давление пропорционально плотности, то есть обратно пропорционально объему, за­нимаемому определенной массой газа (закон Бойля— Мариотта)!

Если нагревать газ при постоянном давлении; то про­
изведение остается неизменным. Это означает, что объ­
ем газа растет пропорционально абсолютной температу­
ре (закон Гей-Люссака).;

Пользуясь уравнением состояния газа, можно, зная любые два показателя (параметра), вычислить Третий. Пусть, например, температура воздуха равна 15^е С, а давление 760 мм рт. ст., что соответствует 10332 кг/м² (1 мм рт. ст. ≈ 13,6 мм вод. ст.=13,6 кг/м²). Тогда мож­но определить плотность газа:

Такие расчеты представляют практический интерес, так как давление и температура могут быть просто из­мерены приборами, в отличие от плотности.

Основные физические свойства воздуха

Воздух характеризуется следующими физическими свойствами: цвет, прозрачность, электропроводимость, звукопроводимость, инертность, вязкость, сжимаемость.

При движении крыла в воздухе возникают силы, ко­торые называют аэродинамическими. Их образование связано с такими физическими свойствами воздуха, как инертность, сжимаемость и вязкость.

Инертностью называется стремление тела сохранять состояние покоя или прямолинейного и равномерного движения. Мерой инертности тела является масса. Инертность воздуха оценивается его массовой плот­ностью, с увеличением которой инертность воздуха воз­растает.

Сжимаемостью называется свойство среды увеличи­вать свою массовую плотность при повышении давления и уменьшать плотность при его понижении. Сжимаемость характеризуется отношением изменения плотности

к изменению давления , то. есть величиной

Чем больше это отношение, тем больше сжимаемость, и

наоборот.

Вязкостью называется свойство среды сопротивлять­ся сдвигу одних ее слоев относительно других (сосед­них), проявляющееся в возникновении между слоями внутреннего трения.

Вязкость присуща различным средам. Однако при­рода вязкости жидкости и газа различна. У жидкости вязкость обусловлена сцеплением молекул. Поэтому, на­пример, при нагревании, когда силы сцепления ослабе­вают, вязкость жидкости уменьшается (скажем, вязкость масла в двигателе).

Вязкость воздуха объясняется обменом молекулами между соседними слоями. Выделим в, воздушном потоке

 

Рис. 1. Внутреннее трение в воздухе

два параллельных направлению движения очень тонких слоя, расстояние между серединами которых равно (рис. 1), причем средняя скорость одного из них больше средней скорости другого на величину На-

ходясь в беспорядочном движении, молекулы из слоя 1 попадают в слой 2 и, теряя там избыток скорости

, стремятся ускорить движение слоя 2, а более «мед­ленные» молекулы из слоя 2, попадая в слой 1, притор­маживают его движение. Нагрев воздуха ускоряет бес­порядочное движение молекул и усиливает обмен ими между слоями, ввиду чего внутреннее трение возраста­ет, а не уменьшается, как в жидкости.

Если поверхность, разделяющую слои 1 и 2, пересе­кают только беспорядочно движущиеся молекулы, а не целые струйки, то сила внутреннего трения между эти­ми слоями, приходящаяся на 1 м² разделяющей поверх­ности, выражается следующей формулой

■ ■

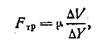
где µ, — коэффициент вязкости, зависящий только от температуры воздуха; при повышении температуры от 20 до 180°С он увеличивается более чем на 30%. Отно-

шение называется градиентом скорости и характе-

ризует интенсивность изменения скорости поперек на-правления движения. Чем резче нарастает скорость от слоя к слою, тем сильнее между ними трение.

Инертность воздуха в воздушном потоке, Уравнение расхода. Закон Бернулли

Из определения термина «инертность» вытекает, что инертность воздуха, рассматриваемого как сплошная среда, может проявиться лишь в том случае, когда, его частицы; испытывают изменения величины или сопро­тивления скорости. При этом инертность проявляется в виде понижения или повышения давления.

Закон постоянного секундного расхода воздуха яв­ляется важнейшим законом теоретической аэродинами­ки. Он формулируется так: при установившемся движе­нии газа через любое поперечное сечение данной струй­ки за одну секунду проходит одна и та же масса газа (рис. 2).

Поскольку

но, так как мы рассматриваем уравнение при малых скоростях (дозвуковых), когда воздух несжимаем, то

Из данного урав­нения вытекает очень важный практический вывод: чем меньше поперечное сечение данной струйки, тем скорость воздуха в нем больше, и наоборот, чем больше попереч­ное сечение струйки, тем скорость в нем меньше.

По частицы воздуха обладают инертностью (имеют массу) и, в соответствии со вторым законом Ньютона, могут получать ускорение только под действием силы, направленной в сторону движения. Значит, на рассмат­риваемом участке струи давление в сечении I должно быть больше, чем в II. Итак, наименьшее давление полу­чается там, где скорость наибольшая, и наоборот. В этом состоит сущность закона Бернулли.

Если предположить, что обмена энергией между стру­ей воздуха и окружающей средой в сечениях I и II нет, то сумма всех видов энергии воздуха в сечении I равна сумме всех видов энергии в сечении II, то есть:,.

где полная энергия — сумма кинетической и

потенциальной энергий.

При условии, что через сечения I и II проходит мас­са воздуха в 1 м³, кинетическую энергию

Рис. 2, К уравнению рас­хода: F₁,F₂ — попереч­ные сечения; ρ₁ ρ₂— плотность; m₁, m₂ — мас­са воздуха, проходящая через сечение за секунду

можно выразить произведением плотности (ρ) на квад­рат скорости, так как масса 1 м³ воздуха есть его плот­ность

Потенциальная энергия состоит из энергии давления, тепловой энергии и энергии силы веса. При условии, что воздух несжимаем, между струйкой и внешней средой отсутствует теплообмен, а энергией силы веса за незна­чительностью ее можно пренебречь, потенциальная энер­гия 1 м³ воздуха будет равна статическому давлению (Р_сг). Произведя соответствующую замену, мы полу­чим уравнение Бернулли для газа и жидкости без учета сжимаемости:

Величина называется скоростным напором

Из уравнения следует, что сумма скоростного напора и статического давления одинакова во

всех сечениях потока идеального несжимаемого воздуха
и есть величина постоянная,

Уравнение Бернулли широко используется для вы­числения картины распределения давления на поверх­ности крыла, при определении скорости полета с по­мощью приемников воздушного давления и при решении

 

других задач гидравлики, гидротехники и аэродинамики. При больших скоростях движения потока, порядка 0,6 от скорости звука и более, пользуются более слож­ной формулой уравнения Бернулли, учитывающей сжи­маемость воздушной среды.

Краткая характеристика атмосферы Земли

Атмосфера Земли имеет сложную структуру. Основ­ными ее слоями являются тропосфера, стратосфера и ионосфера. Это разделение основано на учете как фи­зических свойств отдельных слоев, так и характера их изменения с высотой.

Тропосфера— ближайший к поверхности земли слой
атмосферы. Ее толщина около 8—10 км над полюсами,
16—18 км над экватором и изменяется в зависимости от
времени года, температуры и характера подстилающей
поверхности, а также от характера атмосферных про­
цессов.

Все характеристики тропосферы испытывают суточ­ные и годовые изменения, обусловленные вращением Земли вокруг оси и обращением ее вокруг Солнца. Тро­посфера, особенно ее нижняя половина, является слоем, где протекают и развиваются все жизненные биологиче­ские процессы. Здесь же в основном проводится в на­стоящее время и работа парашютистов. В тропосфере сосредоточен почти весь водяной пар и здесь осущест­вляется непрерывный его круговорот (испарение, кон­денсация и кристаллизация с облакообразованием). Температура (t), атмосферное давление (Р) и плотность (ρ) воздуха понижаются с высотой (температура в среднем на 6,5° С на каждый километр, давление в сред­нем на 1мм через каждые 10 м).

Между слоями тропосферы и стратосферы лежит
тонкий слой, называемый тропопаузой.
Стратосфера— слой атмосферы над тропопаузой при­
мерно до высоты 82—83 км. Характеризуется более мед­
ленным изменением температуры с высотой, чем в тро­
посфере. Стратосферу подразделяют на нижнюю (До
высоты 32—40 км) и верхнюю, простирающуюся от это­
го уровня до 82—83 км.
Нижняя стратосфера характеризуется зимой (по
крайней мере, в средних и высоких широтах) медленным

 

 

понижением температуры с высотой (2° или несколько менее на 1 км), а летом таким же медленным ее рос­том. Поэтому нижнюю стратосферу рассматривают как изометрический слой.

Верхняя стратосфера более сложна по термической структуре, так как включает в себя слой с повышенным содержанием озона (0₃) —озоносферу, начинающуюся примерно от 17—20 км и простирающуюся до 50—55 км. Сильное поглощение озоном ультрафиолетовой радиации солнца обусловливает значительное повышение темпе­ратуры, особенно в верхней ее части (примерно от 35 до 55 км) до максимального значения около 80° С на высоте приблизительно 55 км. Выше начинается посто­янное понижение температуры (в среднем 4,4° С на каждый километр). В результате на высоте 82—83 км температура достигает примерно —35° С. На верхней границе этого холодного слоя плавают серебристые об­лака, что говорит о начале (уже в ионосфере) устойчи-вого роста температуры воздуха с высотой.

Ионосфера — слой атмосферы, расположенный на вы­соте примерно от 80 до 500 км и содержащий большое количество заряженных электричеством частичек, назы­ваемых ионами. Это ионизированные молекулы и атомы атмосферных газов и свободные электроны. Они созда­ют очень высокую проводимость воздуха, что ведет к преломлению, отражению, поглощению и поляризации радиоволн. В частности, это обусловливает слышимость радиосигналов даже незначительной мощности на боль­шие расстояния.

В ионосфере наблюдаются полярные сияния, свече­ния ночного неба, а также магнитные бури.

Температура в ионосфере растет с высотой до очень больших значений, что обусловлено высокими скоростя­ми движения ионизированных молекул и атомов атмос­ферных газов и свободных электронов (кинетическая температура). Ниже приводится схема строения атмос­феры Земли с кривыми изменения температуры (t °С), давления (Рст), направления и скорости перемещения воздушных масс (рис. 3).

Рис. 3. Схема строения атмосферы Земли

 

Стандартная атмосфера

Температура и давление, а следовательно, и плот­ность воздуха, окружающего земной шар, зависят от ряда факторов.

Чем больше высота, тем меньше вес столба выше расположенного воздуха, а значит, меньше давление. Это обстоятельство используется при измерении в по­лете высоты барометрическим высотомером: та или иная высота соответствует определенному давлению воздуха.

Уменьшение давления сопровождается и уменьшени­ем плотности (Р = 286 ρ Т), причем темпы снижения этих показателей по мере увеличения высоты не совпадают, потому что одновременно изменяется и температура воз­духа. Температура и давление воздуха на данной высо­те зависят от географических координат, времени года и суток, от погоды. В результате многочисленных наб­людений и исследований установлены некоторые средние значения изменения с высотой температуры и давления воздуха, а следовательно, и его плотности, которые при­няты в качестве стандартных. Соответствующие данные в виде таблицы стандартной атмосферы широко исполь­зуются при аэродинамических расчетах, градуировке авиационных приборов и т. д.

Таблица стандартной атмосферы

 

 

Бы-	Тем­пера­тура	Массо­вая плот­ность	Давле­ние Р, кг-с2	Отно­ситель­ное давле-	Отно­ситель­ная плот-	Скорое ка на высоте	гь зву-данной а
та
Я, и	t C		м4	ние	ность
		ха, ρ, кг/м2		Р/Ро	ρ/ρо	м/с
	15,00		0,1249	1,000	1,000	340,4
	11,75		0.1190	0,942	0,953	338,5
	8,50		0,1134	0,887	0,907	336,6
	5,25		0,1079	0,835	0,864	334,6
	2,00		0,1026	0,785	0,882	332,7
	—1,25		0,0976	0,737	0,781	330,7
	—4,50		0,0927	0,692	0,742	328,7
	—7,75		0,0880	0,649	0,705	326,7
	—11,00	628S	0,0835	0,608	0,669	324,7
	— 14,25		0,0792	0,570	0,634	322,7
	— 17,50		0,0751	0,533	0,601	320,7
	—20,75		0,0711	0,498	0,569	318,6

 

	—24,00		0,0673	0,466	0,539	316,6
	—27, 25		0,0636	0,435	0,509	314,5
	—30,50		0,0601	0,405	0,481	312,4
	-33,75		0,0568	0,378	0,454	310,3
8ООО	—37,00		0,0536	0,351	0,429	308,2
	—40,25		0,0505	0,327	0,404	306,1
	—43,50		0,0476	0,303	0,381	303,9
(1500	—46,75		0,0448	0,282	0,358	301,8
	—50,00		0,0421	0,261	0,337	299,6
	—53,25		0,0395	0,242	0,317	297,4
	—56,50		0,0371	0,223	0,297	295,2
	—56,50		0,0343	0,206	0,275	295,2
	—56,50		0,0317	0,191	0,254	296,2
	—56,50		0,0293	0,176	0,235	295,2
	—56,50		0,0271	0,163	0,217	295,2
	—56,50		0,0250	0,151	0,200	295,2 1
14 ООО	—56,50		0,0231	0,139	0,185	295,2.
14 500	—56,50		0,0214	0,129	0,171	295,2
	—56,50		0,0197	0,119	0,158	295,2
	. —56,50		0,0183	0,110	0,146	295,2
	—56,50		0,0169	0,102	0,135	295,2.
	—56,50		0,0156	0,094	0,125	295,2
	—56,50		0,0144	0,087	0,115	295,2
	—56,50		0,0133	0,080	0,107	295,2
	—56,50		0,0123	0,074	0,099	295,2
! 8500	—56,50		0,0114	0,068	0,091	295,2
	—56,50		0,0105	0,063	0,084	295,2
	—56,50		0,0097	0,058	0,078	295,2
	—56,50		0,0097	0,054	0,072	295,2
	—56,50		0,0077	0,046	0,061	295,2
	—56,50		0,0065	0,039	0,052	295,2
	—56,50		0,0056	0,034	0,045	295,2
	—56,50		0,0048	0,029	0,038	295,2
	—56,50		0,0041	0,025	0,033	295,2

Как видно из таблицы, на уровне моря (или у по­верхности земли) стандартными атмосферными условия­ми являются: температура t = + l5°С (Т=288 абс), ба­рометрическое давление Р= 10332 кг/м² и плотность воздуха ρ≈ 0,125 кг-с²/м⁴. В нижнем слое земной атмосферы—тропосфере, ко­торая в стандартных условиях простирается, до высоты //=11 км, температура по мере подъема уменьшается па 6,5° С на каждый километр высоты. Выше, где начи­нается стратосфера, температура до высоты 25—30 'км считается постоянной. и равной —56,5° С. Стандартные характеристики атмосферы для больших высот в нашем случае не нужны. Но следует упомянуть, что согласно

данным исследований атмосферы с высоты 25—30 км температура начинает возрастать, достигая на высотах около 50 км величины, близкой к 0°С. Далее начинается новое понижение температуры, и на высоте 70—90 км она равна приблизительно —75° С. Выше 90 км темпе­ратура опять начинает повышаться, становясь на высо­те 200 км более +500° С.

Уменьшение плотности воздуха с высотой означает увеличение средней длины свободного пробега молекул, У земли эта длина составляет около 0,1 микрона, а на высоте 200 км выражается сотнями метров.

Если для высот, исчисляемых немногими десятками километров, длины свободного пробега молекул настоль­ко малы, что можно рассматривать воздух как сплошную среду, то на высотах более 100 км эти длины становятся соизмеримыми с длиной летательного аппарата или да­же могут быть значительно больше. В таких условиях воздушная среда практически состоит из свободных мо­лекул, то есть таких, воздействие которых на летатель­ный аппарат почти не связано с их взаимодействием между собой. Как показали теоретические исследования, некоторые особенности аэродинамики, связанные с уве­личением длины свободного пробега молекул, могут про­являться уже при полетах на высотах более 40 км.

Г л а в а II.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: