 |
Сложение комплексных чисел
|
|
|
|
Пример 1
Сложить два комплексных числа 
, 
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: 
– от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел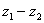 
и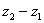 
, если 
, 
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: 
. Для наглядности ответ можно переписать так: 
.
Рассчитаем вторую разность:
Здесь действительная часть тоже составная: 
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: 
. Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел 
, 
Очевидно, что произведение следует записать так:
Следует раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
|
|
|
Я распишу подробно:
Надеюсь, всем было понятно, что 
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: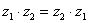 
.
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4
Даны комплексные числа 
, 
. Найти частное 
.
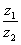Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем формулу 
и смотрим на наш знаменатель: 
. В знаменателе уже есть 
, поэтому сопряженным выражением в данном случае является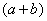 
, то есть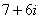 
Согласно правилу, знаменатель нужно умножить на 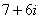, и, чтобы ничего не изменилось, домножить числитель на то же самое число :
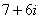Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).
Распишу подробно:
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде 
.
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: 
. Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: 
. Для любителей порешать приведу правильный ответ: 
Пример 5
Дано комплексное число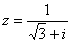 
. Записать данное число в алгебраической форме (т.е. в форме 
).
Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть 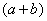, поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на 
:
|
|
|
Пример 6
Даны два комплексных числа 
, 
. Найти их сумму, разность, произведение и частное.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
|
|
|
