 |
2.1 Расчет дебита многоствольной скважины
|
|
|
|
2. 1 Расчет дебита многоствольной скважины
Задача 2. 1
Одной из первых и наиболее упоминаемой в литературных источниках зависимостей, описывающих приток к многоствольной горизонтальной скважине, с равномерном веерным расположением в центре круговой залежи, является уравнение Борисова Ю. П., Пилатовского В. П., Табакова В. П.:
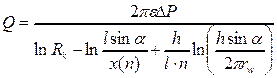, (2. 1)
где, п — число стволов, а — угол наклона ствола от вертикали, l — длина отдельного ствола, функция х(п)равна 4; 2; 1. 86; 1. 78 при числе горизонтальных стволов 1; 2; 3 и 4.
Григулецкий В. Г., Никитин Б. А. анализировали влияние различных факторов на дебит многоствольной горизонтальной одноярусной скважины, учитывающей анизотропность пласта:
, (2. 2)
где b — параметр анизотропии проницаемости пласта.
Для одноярусной многоствольной горизонтальной скважины известно также уравнение:
, (2. 3)
Если принять n=2, то получим формулу Джоши, в которой вместо малой полуоси эллипса используется радиус контура питания, а для описания течения к точечному стоку уравнение Борисова Ю. П.
Для данных геолого-физических условий пласта, представленных в таблице 2. 1 рассчитать дебит скважины с многоствольным окончанием при числе горизонтальных стволов n=1; 2; 3; 4, сопоставить полученные результаты.
Таблица 2. 1 - Характеристика скважины и пластовой системы
| Наименование параметра | Условное обозначение | Единицы измерения (СИ) | Значение |
| Длина горизонтального участка | l | м | |
| Проницаемость по горизонтали, м2 | kh | м2 | 147·10-15 |
| Проницаемость по вертикали, м2 | kv | м2 | 36·10-15 |
| Вязкость нефти | μ н | Па·с | 0, 00098 |
| Пластовое давление | Рпл | Па | 23, 1·106 |
Продолжение таблицы 2. 1
|
|
|
| Забойное давление | Рзаб | Па | 16·106 |
| Радиус горизонтального участка скважины | rc | м | 0, 1 |
| Радиус контура питания | Rk | м | |
| Угол наклона ствола от вертикали | α | град | |
| Толщина продуктивного пласта | h | м |
Задача решается следующим порядком:
1. Находится значение гидропроводности и анизотропии пласта:
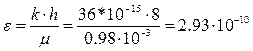(м2·м)/(Па·с)
2. Расчитываем приток жидкости к многоствольной горизонтальной скважине с n=1 по уравнению Борисова Ю. П., Пилатовского В. П., Табакова В. П. по формуле 2. 1:
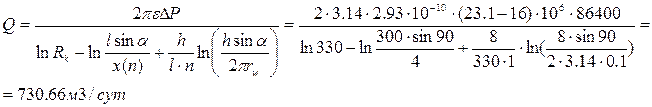
3. Расчитываем приток жидкости к многоствольной горизонтальной скважине с n=1 по уравнению Григулецкого В. Г., Никитина Б. А. по формуле 2. 2:
4. Расчитываем приток жидкости для одноярусной многоствольной горизонтальной скважине с n=1 по формуле 2. 3:
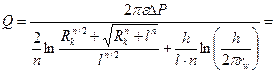
5. Проводя анологичный расчет для n = 2; 3 и 4, получаем:
| n | Методика | ||
| Борисова, м3/сут | Григулецкого, м3/сут | Одноярусная, м3/сут | |
| 730, 7 | 760, 3 | 596, 2 | |
| 1376, 6 | 1429, 2 | 1150, 2 | |
| 1533, 0 | 1576, 0 | 1665, 0 | |
| 1643, 4 | 1680, 3 | 2143, 6 | |
2. 2 Задача для самостоятельного решения
Задача 2. 2
Для данных геолого-физических условий пласта, представленных в таблице 2. 2 рассчитать дебит скважины с многоствольным окончанием при числе горизонтальных стволов n=1; 2; 3; 4, сопоставить полученные результаты, сделать выводы. Принять для всех вариантов угол наклона ствола от вертикали - α =90 градусов.
Таблица 2. 2 - Характеристика скважины и пластовой системы
| Вариант | Длина ГС, м | h, м | Kh·10-15, м2 | Кv·10-15, м2 | Вязкость, мПа∙ с | Рпл, МПа | Рзаб, МПа | Радиус скв, м | Rk, м | |||
| 1, 12 | 17, 5 | 0, 1 | ||||||||||
| 1, 16 | 0, 1 | |||||||||||
| 1, 16 | 0, 1 | |||||||||||
| 1, 16 | 21, 8 | 0, 1 | ||||||||||
| 0, 98 | 21, 1 | 13, 7 | 0, 1 | |||||||||
| 0, 98 | 23, 1 | 0, 1
| ||||||||||
| 0, 98 | 23, 3 | 0, 1 | ||||||||||
| 0, 51 | 0, 1 | |||||||||||
| 0, 41 | 24, 3 | 5, 8 | 0, 1 | |||||||||
| 0, 41 | 24, 3 | 11, 2 | 0, 1 |
3. 1 Расчёт предельной безводной депрессии скважины с горизонтальным окончанием
Задача 3. 1
Как показывают анализы расчетов, предельные безводные дебиты для однородных пластов малы и практически не приемлемы. Большой практический и теоретический интерес представляют задачи продвижения границ раздела нефть – вода к забою скважины (нестабильный конус воды). Этой проблеме посвящен ряд работ как отечественных, так и зарубежных исследователей. Известны работы акад. П. Я. Полубариновой–Кочиной, под руководством которой в институте механики АН СССР проведена серия экспериментальных работ на щелевых моделях по изучению плоского движения в пористых средах, в том числе и опыты по продвижению конуса воды в однородном пласте (рис. 3. 1).
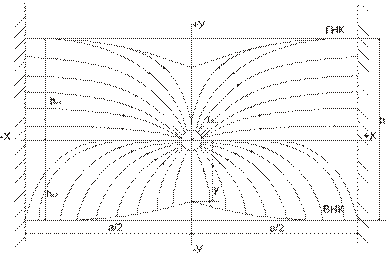
Рисунок 3. 1 - Схема притока к горизонтальному стволу скважины в бесконечном пласте по протяженности вдоль оси z, расположенной симметрично между двумя проницаемыми вертикальными плосткостями, обусловленного вытеснением нефти подошвенной водой (плосткость у=0 является кровлей нефтяной залежи). Схема притока к горизонтальному стволу скважины, обусловленного вытеснением нефти газом (плосткость у=h) является подошвенной нефтегазовой залежи.
Для данных геолого-физических условий пласта, представленных в таблице 3. 1 рассчитать предельную депрессию конусообразования.
Таблица 3. 1 - Характеристика скважины и пластовой системы
| Наименование параметра | Условное обозначение | Единицы измерения (СИ) | Значение |
| Нефтенасыщенная толщина | b | м | 4, 6 |
| Проницаемость по горизонтали | kh | м2 | 270·10-15 |
| Проницаемость по вертикали | kv | м2 | 100·10-15 |
| Вязкость нефти | μ н | Па·с | 0, 00098 |
Продолжение таблицы 3. 1
| Радиус горизонтального участка скважины | rc | м | 0, 1 |
| Радиус контура питания | Rk | м | |
| Плотность нефти | ρ н | кг/м3 | |
| Плотность воды | ρ в | кг/м3 | |
| Мощность пласта | h | м | 18, 9 |
Задача решается следующим порядком:
1. Определим коэффициент анизотропии пласт:
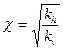(3. 1)
|
|
|
где kh – горизонтальная составляющая проницаемости пласта,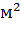 
; kv – вертикальная составляющая проницаемости пласта,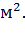 
2. Определим безразмерные параметры ρ 0 и ħ:
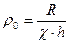(3. 2)
где R – радиус контура питания скважины, м; h – мощность пласта, м.
(3. 3)
где b – нефтенасыщенная толщина пласта, м.
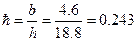
3. По таблице 3. 2 определяем безразмерный дебит:
q (ρ 0; ħ ) = q (8; 0, 243) = 0, 14
4. Определим безразмерную ординату вершины водяного конуса:
ξ 0 (ρ 0; ħ ) = ξ 0 (8; 0, 243) = 0, 64
5. Определим высоту водяного конуса:
y0 = (1- ξ 0)·h
y0 = (1-0, 64)·18, 9=6, 8 м
6. Определим дебит скважины:
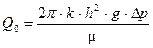(3. 4)
где k – горизонтальная составляющая проницаемости, 
h – мощность пласта, м; g – ускорение свободного падения, м/ 
; △ ρ – разность плотностей воды и нефти, кг/ 
; µ - динамическая вязкость нефти, Па·с
△ ρ = ρ в –ρ н = 992 – 742 = 250 кг/ 
Таблица 3. 2 - Результаты определения предельных безводных дебитов
| 
| 
| 
| 
|
|
|
|
|
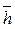
| 0, 2 | 1, 0 | 0, 455 | 0, 450 | 1, 233 | 0, 6 | 0, 585 | 0, 175 | 2, 371 |
| 0, 3 | 0, 475 | 0, 500 | 1, 050 | 0, 625 | 0, 190 | 1, 973 | ||
| 0, 4 | 0, 540 | 0, 545 | 0, 844 | 0, 630 | 0, 240 | 1, 541 | ||
| 0, 5 | 0, 610 | 0, 574 | 0, 679 | 0, 685 | 0, 300 | 1, 050 | ||
| 0, 6 | 0, 710 | 0, 580 | 0, 500 | 0, 735 | 0, 370 | 0, 716 | ||
| 0, 7 | 0, 820 | 0, 590 | 0, 305 | 0, 840 | 0, 3755 | 0, 426 | ||
| 0, 20 | 0, 9 | 0, 470 | 0, 390 | 1, 358 | 0, 5 | 0, 690 | 0, 095 | 3, 263 |
| 0, 3 | 0, 500 | 0, 425 | 1, 176 | 0, 700 | 0, 125 | 2, 400 | ||
| 0, 4 | 0, 550 | 0, 460 | 0, 978 | 0, 715 | 0, 175 | 1, 685 | ||
| 0, 5 | 0, 620 | 0, 510 | 0, 745 | 0, 730 | 0, 240 | 1, 125 | ||
| 0, 6 | 0, 715 | 0, 525 | 0, 542 | 0, 750 | 0, 310 | 0, 806 | ||
| 0, 7 | 0, 825 | 0, 535 | 0, 327 | 0, 845 | 0, 315 | 0, 492 | ||
| 0, 20 | 0, 8 | 0, 510 | 0, 320 | 1, 531 | 0, 4 | 0, 785 | 0, 025 | 8, 600 |
| 0, 3 | 0, 525 | 0, 350 | 1, 357 | 0, 800 | 0, 040 | 5, 600 | ||
| 0, 4 | 0, 575 | 0, 380 | 1, 118 | 0, 805 | 0, 100 | 1, 950 | ||
| 0, 5 | 0, 640 | 0, 440 | 0, 818 | 0, 810 | 0, 165 | 1, 151 | ||
| 0, 6 | 0, 720 | 0, 480 | 0, 583 | 0, 815 | 0, 245 | 0, 755 | ||
| 0, 7 | 0, 830 | 0, 490 | 0, 346 | 0, 850 | 0, 260 | 0, 576 | ||
| 0, 2 | 0, 7 | 0, 550 | 0, 240 | 1, 875 | 0, 3 | 0, 825 | 0, 005 | 35, 00 |
| 0, 3 | 0, 570 | 0, 275 | 1, 563 | 0, 830 | 0, 010 | 17, 00 | ||
| 0, 4 | 0, 600 | 0, 315 | 1, 269 | 0, 900 | 0, 015 | 6, 666 | ||
| 0, 5 | 0, 680 | 0, 375 | 0, 583 | 0, 910 | 0, 075 | 1, 200 | ||
| 0, 6 | 0, 725 | 0, 425 | 0, 647 | 0, 915 | 0, 175 | 0, 485 | ||
| 0, 7 | 0, 835 | 0, 430 | 0, 383 | 0, 920 | 0, 200 | 0, 400 |
|
|
|
7. Определим предельный безводный дебит:
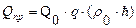(3. 5)
8. Определим значение функции Ψ (ρ 0; ħ ):
9. Определим фильтрационное сопротивление:
(3. 6)
где ħ - безразмерная мощность пласта; Rк – радиус контура питания скважины, м; r – радиус скважины, м; Ψ – безразмерная функция.
10. Определим дополнительное фильтрационное сопротивление:
11. Определим безразмерную депрессию:
(3. 7)
где ε 0 - фильтрационное сопротивление, △ ε - дополнительное фильтрационное сопротивление.
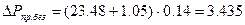
12. Определим предельную депрессию:
(3. 8)
|
|
|
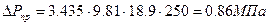
