Цилиндрические зубчатые колёса

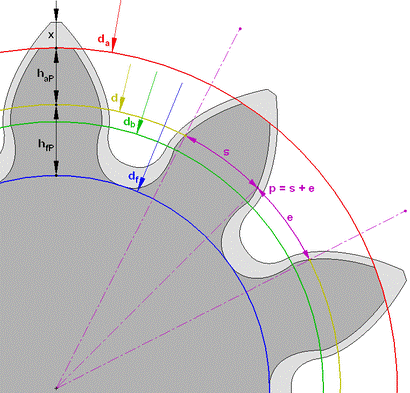
Параметры зубчатого колеса

[править] Поперечный профиль зуба

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако, существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

• m — модуль колеса, тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

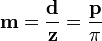
• z — число зубьев колеса
• p — шаг зубьев (отмечен фиолетовым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определенные значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50.

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т.н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с "нулевыми" зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. положительным смещением, а смещение дальше от заготовки наз. отрицательным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

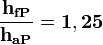
Отсюда получаем, что высота зуба h (на рисунке не обозначена):

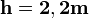
Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

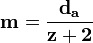
[править] Продольная линия зуба

Зубчатое колесо от часового механизма

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

• прямозубые
• косозубые
• шевронные

[править] Прямозубые колёса

Прямозубые колёса

Прямозубые колёса — самый распространённый вид зубчатых колёс. Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, но, в то же время, предельный крутящий момент таких колес ниже, чем косозубых и шевронных.

[править] Косозубые колёса

Косозубые колёса

Косозубые колёса являются усовершенствованным вариантом прямозубых. Их зубья располагаются под углом к оси вращения, а по форме образуют часть спирали.

• Достоинства:
• Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом.
• Площадь контакта увеличена по сравнению с прямозубой передачей, таким образом, предельный крутящий момент, передаваемый зубчатой парой, тоже больше.
• Недостатками косозубых колёс можно считать следующие факторы:
• При работе косозубого колеса возникает механическая сила, направленная вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;
• Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.

В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.

[править] Шевронные колеса

 

Шевронные колёса

Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Передачи, основанные на таких зубчатых колёсах, обычно называют «шевронными».

Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).

[править] Зубчатые колёса с внутренним зацеплением

При жёстких ограничениях на габариты, в планетарных механизмах, в шестерённых насосах с внутренним зацеплением, в приводе башни танка, применяют колёса с зубчатым венцом, нарезанным с внутренней стороны. Вращение ведущего и ведомого колеса совершается в одну сторону. В такой передаче меньше потери на трение, то есть выше КПД.

[править] Секторные колёса

Секторное колесо представляет собой часть обычного колеса любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.

[править] Колёса с круговыми зубьями

Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.

[править] Конические зубчатые колёса

Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с прямым зубом, например, применяются в автомобильных дифференциалах, используемых для передачи момента от двигателя к колёсам.

 

23.

Делительная окружность, окружность зубчатого колеса, на которой его шаг и угол зацепления соответственно равны теоретическому шагу и углу зацепления инструмента (например, рейки)

Начальная окружность — это расчетная (условная) окружность, по которой как бы происходит соприкасание зубьев колес, находящихся в зацеплении. По начальной окружности нормируют и проверяют толщину зуба

26. Понятие об исходном контуре рейки. Как было показано выше, частным случаем эвольвенты при z = (бесконечность) является прямая линия. Это дает основание использовать в эвольвентном зацеплении рейку с прямобочными зубьями. При этом любое зубчатое колесо данного модуля независимо от числа зубьев может быть сцеплено с рейкой того же модуля. Отсюда возникла идея обработки колес методом обкатки. В зацеплении колеса с рейкой (рис. 1.2) радиус начальной окружности последней равен бесконечности, а сама окружность превращается в начальную прямую рейки. Линия зацепления N₁N₂Так как профиль зубьев рейки - прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.4, а) проходит через полюс Р касательно к основной окружности колеса и перпендикулярно к боковой стороне профиля зуба рейки. В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α.

Так как профиль зубьев рейки - прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.3, а)

В соответствии со стандартами, принятыми в нашей стране для эвольвентного зацепления, исходный контур имеет следующие параметры зубьев в зависимости от модуля:

• угол профиля α = 20°;
• коэффициент высоты головки h^*_a = 1;
• коэффициент высоты ножки h^*_f = 1,25;
• коэффициент радиального зазора с^* = 0,25 или 0,3;
• коэффициент граничной (рабочей) высоты зуба h^*_L = 2;
• шаг зубьев Р = π · m;
• толщина зуба S и ширина впадины е: S = е = 0,5Р = π · m / 2.

Делительная прямая рейки проходит по середине рабочей высоты зуба h_L.

Для зуборезных инструментов основные параметры зубьев по аналогии с изложенным выше задаются параметрами исходной инструментальной рейки (рис. 1.3, б). Так как зубья режущего инструмента обрабатывают впадину между зубьями колеса и могут нарезать колеса с модифицированным (фланкированным) профилем, между названными исходными контурами имеются существенные различия.

1. Высота головки зуба исходной инструментальной рейки h_a0 = (h^*_f0 + с₀)m = 1,25 m, т.е. коэффициент высоты головки й h^*_a0 =1,25. Высота ножки зуба h_f0 = 1,25 m, а полная высота зуба h₀ = h_a0 + h_f0 = 2,5 m.
2. Если нарезаемое колесо имеет срез у головки (модифицированный профиль), то ножка зуба инструментальной рейки должна иметь утолщение с параметрами h _{ф 0}, α _{ф 0}, n _{ф 0}.
3. Толщина зуба у зубчатой рейки S = ^{π · m} / ₂, а у инструментальной рейки при нарезании колес с модифицированным профилем зубьев S₀ = ^{π · m} / ₂ ± ΔS₀

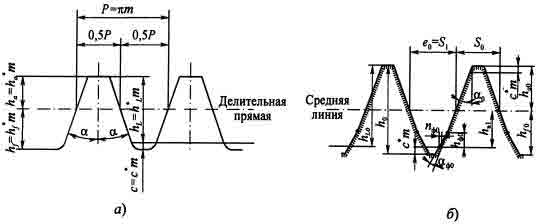
Рис. 1.3. Исходные контуры:
а - зубчатой рейки; б - инструментальной рейки

Поправка ΔS ₀ берется из справочников [23, 24] в зависимости от величины модуля зуба. Знак "+" берется для чистовых, а знак "-" - для черновых инструментов. В первом случае происходит утонение зубьев нарезаемого колеса с целью создания бокового зазора между зубьями сцепляемых колес, во втором случае утолщение, в результате чего нарезаемые зубья получают припуск на чистовую обработку.

У колес с обычным (модифицированным) профилем зубьев изменение толщины нарезаемых зубьев можно получить путем смещения инструментальной рейки относительно центра колеса и утолщение ее зубьев у ножки не требуется.

Параметры зацепления корригированных зубчатых колес. Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.

Применительно к долбякам корригирование дает возможность получения задних углов на режущих кромках (см. ниже).

Из известных методов корригирования на практике наибольшее применение нашло высотное корригирование, которое осуществляется путем смещения профиля исходной инструментальной рейки относительно центра нарезаемого колеса. Такое смещение принято считать положительным, если рейка отводится от центра колеса, и отрицательным, когда она приближается к его центру (рис. 1.4).

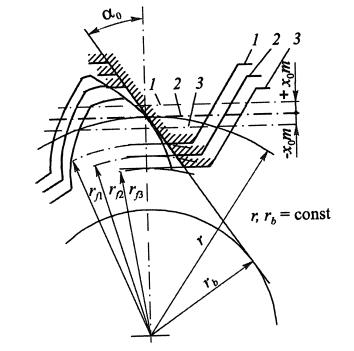
Рис. 1.4. Схема высотного корригирования зубчатого колеса:
1 - положительное смещение; 2 - нулевое смещение; 3 - отрицательное смещение
Величина смещения оценивается произведением х_о · m, где х₀ - коэффициент смещения

При положительном смещении высота головки зуба нарезаемого колеса h^'_a1 увеличивается на величину хот, а высота ножки h^'_f1 уменьшается на ту же величину. При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.

Так как при этом положение делительной и основной окружностей колеса постоянно и не зависит от величины смещения, то неизбежно изменение толщины зуба нарезаемого колеса по делительной окружности из-за смещения делительной прямой рейки относительно начального положения на величину ± х_о · m. Как видно из рис. 1.5, толщина зуба по делительной окружности у корригированного колеса при смещении рейки инструмента

S^'_{1, 3} = ^{π · m} / ₂ ± 2 · x₀ · m · tg α₀

где ΔS = x₀ · m · tg α ₀.

Знак "+" берется при положительном, а знак "-" - при отрицательном смещении.

При расчетах зуборезных инструментов, например долбяков, зубья которых корригированы, возникает необходимость определения толщины зуба на окружности любого радиуса - r_у, концентричной с делительной окружностью радиусом r.

Рис. 1.5. Изменение толщины зуба на делительной окружности при положительном смещении инструментальной рейки.

27-37

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: