Виды зубчатых передач и их свойства

При проектировании зубчатой передачи существенную роль играет выбор ее геометрических параметров. Геометрический расчет зубчатой передачи выполняют при условии, что модуль т зубчатых колес получен из расчета зубьев на прочность.

Цилиндрическая зубчатая передача может быть составлена из колес с прямыми и косыми зубьями. Передачи с косозубыми колесами имеют определенные достоинства, которые следует учи­тывать при проектировании: 1) они имеют высокий коэффициент перекрытия, который определяется рабочей шириной зубчатых колес и может быть практически доведен до 10 и более; 2) их можно выполнить при небольшом числе зубьев колес (практи­чески малое колесо может иметь число зубьев три, теоретически оно может быть доведено до одного). Отрицательным свойством косозубой передачи является наличие осевых сил, что усложняет конструкцию передачи.

Зубчатые передачи с прямыми и косыми зубьями, в соответ­ствии с ГОСТ 16531- 83, могут быть трех видов: без смешения, положительные и отрицательные.

Зубчатая передача без смещения составляется или из зубчатых колес без смещения (х₁ = х₂ = 0), или из одного положительного и другого отрицательного колеса, при условии, что х₁ = - х₂ (так называемая равносмещенная передача). Делительные окружности колес зубчатой передачи без смещения соприкасаются в полюсе зацепления Р и в процессе зацепления перекатываются друг по другу без скольжения, т. е. одновременно являются начальными окружностями колес (рис. 1, а), при этом коэффициент воспринимаемого смешения у равен нулю. Радиусы начальных окружностей равны радиусам делительных окружностей:

r_w= r = mz / 2

Межосевое расстояние, равное сумме радиусов делительных окружностей:

a_w=r₁+r₂=m(z₁+z₂)/2=a, (1.1)

называется делительным межосевым расстоянием, а угол зацепления передачи без смеще­ния a_w= a.

 

Положительная зубчатая передача может быть составлена из двух положительных зубчатых колес (х1,2 > 0) или из одного положительного и другого без смещения, или, наконец, из одного положительного и другого отри­цательного колеса. В последнем случае абсолютное значение коэффициента смещения положительного колеса должно быть больше, чем отрицательного. Делительные окружности колес положительной зубчатой передачи не соприкасаются, поэтому коэффициент воспринимаемого сме­щения у > 0 (рис. 1, б), начальные окружности больше дели­тельных, т.е. межосевое расстояние равно сумме радиусов на­чальных окружностей колес:

(1.2)

При этом a_w > a, а угол зацепления положительной зубчатой передачи a_w>a.

Отрицательная зубчатая передача может быть составлена из двух отрицательных зубчатых колес или из одного отрицательного и другого колеса без смещения, или же из одного отрицательного и другого положительного колеса. В последнем случае коэффициент смещения отрицательного зубчатого колеса должен быть по абсолютному значению больше, чем положительного. Делительные окружности отрицательной зубчатой передачи пересекаются (рис. 1, в). Радиусы делительных окружностей больше радиусов начальных окружностей (r > r_w). Воспринимаемое смещение у этой передачи отрицательное; межосевое расстояние определяют по той же формуле, что и для положительной передачи:

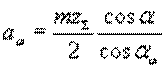
Для отрицательной передачи a_w < a и a_w < a.

При проектировании следует учитывать особенности каждого вида передач. Наилучшими качествами обладают положительные зубчатые передачи: у них больше радиусы кривизны боковых поверхностей зубьев и при тех же передаточном числе и модуле они могут иметь меньшие габаритные размеры и массу. При проектировании следует учитывать особенности каждого вида передач. Наилучшими качествами обладают положительные зубчатые передачи: у них больше радиусы кривизны боковых поверхностей зубьев и при тех же передаточном числе и модуле они могут иметь меньшие габаритные размеры и массу.

Эксплуатационные показатели у передач без смещения хуже, чем у положительных, однако в настоящее время они достаточно часто применяются в машинах, так как очень просто рассчитываются и удовлетворяют принципу сменности колес, Отрицательную передачу, имеющую наихудшие эксплуатационные показатели, применяют, как правило, когда задано межосевое расстояние.

 

 

§ 2. Исходный производящий контур инструмента и станочное зацепление

 

Геометрия проектируемой передачи определяется параметра­ми исходного контура инструмента и его смещениями при нарезании колес передачи. Поэтому при проектировании прежде всего следует задать исходный производящий контур инструмента и выбрать расчетные смещения.

Если цилиндрическое зубчатое колесо нарезается реечным инструментом, то станочное зацепление рассматривают в торцо­вой плоскости, перпендикулярной оси зубчатого колеса. Такое зацепление является зацеплением реечного исходного производящего контура с нарезаемым колесом.

Реечный исходный производящий контур, в соответствии с ГОСТ 13755-81, - это контур зубьев в нормальном или торцовом сечении производящей рейки плоскостью, перпендикулярной к ее делительной плоскости.

Параметры исходного производящего контура стандартизирова­ны. На рис. 2 изображен исходный производящий контур для наре­зания цилиндрических эвольвентных колес с модулем от 1 мм и более по ГОСТ 13755-81. Это прямобочный реечный контур с рав­номерно чередующимися симметричными зубьями и впадинами; переход от профиля зуба к линии впадин очерчен дугой окружности.

Стандартом установлены следующие параметры и коэффици­енты исходного контура: угол главного профиля a = 20°; коэф­фициент высоты головки зуба h_a^* = 1,0; коэффициент высоты ножки h_f^*= 1,25; коэффициент граничной высоты (т.е. высота прямолинейного участка профиля) h_l^* =2 h_a^*; коэффициент ра­диуса кривизны переходной кривой r_f^* = 0,38; коэффициент ра­диального зазора с^* = 0,25. Абсолютные значения размеров зуба исходного контура получают умножением перечисленных коэф­фициентов на модуль.

Исходный контур для мелкомодульных (0,1 < т < 1,0) колес регламентирован ГОСТ 9587—81. Параметры исходного контура: h_a^* = 1,0... 1,1; c^*= 0,25... 0,40. Переходная кривая может быть выполнена одной дугой радиусом 0,44m (или двумя дугами ради­усом 0,38m) и сопрягающей прямой.

Для нарезания косозубых колес применяют тот же стандарт­ный инструмент, что и для прямозубых, но его устанавливают наклонно к плоскости заготовки. Реечный исходный производя­щий контур в этом случае имеет параметры, зависящие от угла наклона линий зубьев. Эти параметры определяют следующим образом:

угол профиля

(1.3)

шаг

pt = p /cosb;

(1.4)

модуль зубьев

mt = m / cosb

(1.5)

коэффициент высоты головки зуба

h*ta = h*a × cosb

(1.6)

коэффициент радиального зазора

c*t = c* × cosb

(1.7)

Следовательно, зная параметры контура для нарезания пря мозубого колеса: a, m, h^*_a, c^* и угол наклона линии зубьев b, можно подсчитать все параметры реечного исходного производя­щего контура для нарезания косозубых колес: a_t, m_t, h^*_at, c_t^*.

Принципиальная схема станочного зацепления при нарезании косозубого колеса имеет такой же вид, как и при нарезании прямозубого.

Делительная прямая реечного исходного производящего контура в станочном зацеплении может располагаться по отношению к делительной окружности нарезаемого колеса различным образом. При нарезании колеса без смещения делительная прямая контура касается делительной окружности колеса, при нарезании колеса с положительным смещением, она отодвинута от делительной окружности на величину положительного смещения, а при нарезании колеса с отрицательным - придвинута к центру колеса на величину этого смещения. На рис. 2 изображено станочное зацепление при нарезании положительного прямозубого колеса.

В процессе зацепления по делительной окружности колеса перекатывается без скольжения та прямая инструмента, которая параллельна делительной прямой и касается делительной окружности. Эту прямую называют станочно начальной. Шириной впадины инструмента на станочно-начальной прямой определяется толщина зуба колеса по делительной окружности. У колеса без смещения толщина зуба по делительной окружности равна половине шага (s = p т/2), у положительного колеса она больше половины шага (s > p т/2), у отрицательного колеса - меньше (s < p т/2).

 

 

§ 3. Определение модуля

 

В некоторых заданиях на курсовой проект значения модуля зубчатых передач не заданы или выбраны условно, без учета действующих нагрузок в приводе. Выполнив первый лист проекта, студент определяет характер изменения нагрузки (моменты) на входном и выходном валах машинного агрегата. Поэтому при расчете зубчатой передачи рекомендуется по известной нагрузке определить или уточнить модуль.

При проектном расчете зубчатых колес модуль зацепления т, мм, определяют из условия прочности зубьев на изгиб по обобщенной формуле:

(1.8)

где М - момент нагрузки на колесе, Н×м; Y_F - коэффициент, учиты­вающий форму зубьев для зубчатых колес внешнего зацепления (для зубчатых колес с z₁ = 10…17 и 0 < х_t < 0,5, Y_F = 3,5…4,3. Значения коэффициентов формы зубьев в зависимости от числа зубьев и смещения исходного контура, полученные методами теории упругости, приведены в [5, табл. 10.3]); Y_b =1-b /180^° - коэффициент, учитывающий наклон образующей зуба b; К_F - коэффициент нагрузки (К_F= 1,0... 1,2); [s]_F - допускаемые напряжения изгиба (для термообработалных сталей типа 40Х [s] _F = 280..340 МПа); y_m = b_W /т- коэффициент ширины зубчатого венца (для прямозубых колес y_m = 10... 12, для косозубых колес y_m = 12... 20).

Принимая средние значения коэффициентов и [s] _F = 300 МПа, получим:

для косозубых передач

(1.9)

для прямозубых передач

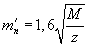
(1.10)

Величины M и z должны характеризовать одно и то же зубчатое колесо, т.е. в формулу следует подставлять значения либо M ₁ и z₁, либо M ₂ и z₂. Если колеса выполнены из одного материала, то расчет обычно ведут по шестерне.

Окончательное значение модуля выбирают, округляя получен­ное при расчете значение т' или т_п' до ближайшего большего значения из ряда стандартных в соответствии с ГОСТ 9563-80:

первый предпочтительный ряд: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20, 25; 32; 40... 100 мм;

второй ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9 мм и т.д.

Модуль колес нужно выбирать минимальным, так как с его увеличением возрастают габаритные размеры и масса передач, трудоемкость обработки. С другой стороны, принимать значении мо дуля меньше 1,5 мм в силовых передачах машин не рекомендуется.

 

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: