Расчет профилей цилиндрических зубчатых колес и геометрии переходной кривой, нарезанных инструментом реечного типа

 

При решении многих вопросов, связанных с расчетом зубчатых зацеплений на ЭВМ и использованием машинной графики, необходимо иметь аналитические выражения для координат профиля зуба как для эвольвентного участка, так и для его нерабочей переходной части, характер которой зависит от способа нарезания и вида применяемого инструмента.

Профили зубьев при на­резании методом огибания содержат три характерных участка (рис. 5): 1) а - а, являющийся огибающим по отношению к профилю зубьев инструмента; 2) b - с, очерченный по дуге окружности и представляющий дно впадины; 3) участок b - а, очерченный так называемой переходной кривой. Переходной поверхностью называют часть боковой поверхности зуба, которая соединяет его главную (эвольвентную) поверхность с поверхностью впадин. Часть профиля зуба, расположенную в пределах его переходной поверхности, называют переходной кривой. Форма переходной поверхности, определяет размеры зуба у основания и характеризует, таким образом, изгибную прочность зуба, а также правильного, без интерференции, зацепления с сопряженным колесом и выполнения некоторых видов отделочных, операций.

Уравнение профиля дает возможность выполнить точное построение профиля в любом требуемом масштабе, не прибегая к графическим способам, описанным в гл. I, § 7. Наличие точных изображений профилей значительно облегчает нахождение коэффициентов концентрации напряжений для зубьев, нарезанных со смещением.

Для построения эвольвентного профиля воспользуемся методикой, изложенной в работе [6]. Пусть имеется прямоугольная система координат (см. рис. 5), ось ординат которой проходит через середину зуба, а начало координат лежит на окружности впадин. В качестве текущего параметра примем не угол развернутости эвольвенты, а угол обкатки инструмента или угол поворота колеса при нарезаний. В предлагаемой системе координат просто выразить толщину зуба и описать переходную кривую профиля зуба колеса, нарезаемого реечным инструментом.

Вывод основных уравнений профиля базируется на методе преобразования координат, отражающем кинематику

образования профиля с помощью инструмента, работающего по методу обкатки. Этот метод нарезания основан на том, что по станочно - начальной (делительной) окружности, являющейся в процессе нарезания центроидой, зуборезный инструмент обкатывается без скольжения с помощью своей центроиды. Центроидой у рейки является прямая, у долбяка - окружность. На рис. 6 изображены расчетная схема станочного зацепления, а также неподвижная x0O1y0 и подвижная x¢A у¢ системы координат. Ось O1y0 неподвижной системы координат проходит через точку Р пересечения профиля с делительной окружностью, а начало координат 01 находится в центре вращения нарезаемого колеса.

Ось Аx¢ подвижной системы координат совпадает с делительной прямой рейки, а начало координат лежит в точке А на режущей кромке ВС инструмента.

Формулы преобразования для перехода от координат x₀O₁y₀ к координатам x¢A у¢ имеют вид

x¢ = x0 cosj - y0 sinj + rj; y¢ = x0 sinj + y0 cosj - r,

(1.42)

или

x0 = (x¢ - rj) cosj + (y¢ + r) sinj; y0 = -(x¢ - rj) sinj + (y¢ + r) cosj.

(1.43)

Координаты точки Э, лежащей на нарезаемой эвольвенте профиля в системе координат x¢A у¢:

xЭ = r×j × sin2j yЭ = r×j × sinj × cosj

(1.44)

Подставляя их в выражение (1.43), получим уравнение эвольвентного профиля в системе х₀ 0₁ у₀:

x0Э = r [ sinj - j cosa cos(j + a) ] y0Э = r [ cosj - j cosa sin(j + a) ]

(1.45)

Перейдем теперь к упомянутой ранее системе координат хOу (см. рис. 5), ориентированной относительно середины зуба. Формулы перехода от системы х₀ 0₁ у₀

x = x0 cosy - y0 siny y = y0 siny + y0 cosy - rf

(1.46)

где y = s /(2r) - половина угловой толщины зуба на делительной окружности; r_f - радиус окружности впадин нарезаемого колеса.

С учетом уравнений (1.43) и (1.46) формулы для перехода в систему хОу предстанут в следующем виде:

x = (x¢ - rj) cos(j - y) + (y¢ + r) sin(j - y); y = -(x¢ - rj) sin(j - y) + (y¢ + r) cos(j - y) – rf;

(1.47)

а в системе х' Ау' уравнение эвольвенты будет иметь такую форму:

xЭ = r [ sin(j - y)-j cosa cos(j - y + a) ]; yЭ = r [ cos(j - y)+j cosa sin(j - y + a) ] – rf;

(1.48)

Угол j для различных точек профиля эвольвент будет принимать следующие значения:

j_p = j_III = 0; j_H = j_а = - tga; j_IV = tga_a - tga.

Переходная поверхность формируется при нарезании зубьев, поэтому ее геометрия зависит от типа и геометрии применяемого инструмента, а также от параметров станочного зацепления. Ниже рассмотрена геометрия переходной кривой, подучаемой при использовании инструмента с кромкой зуба, очерченной дугой окружности радиусом r_f, или прямой (фаской).

При нарезании колеса рейкой с угловыми точками профиля (с фаской) на вершине зубьев переходная часть профиля представляет собой траекторию угловой точки при обкатывании инструмента по делительной окружности нарезаемого колеса.

Выпишем в системе х' Ау' (рис.7) координаты угловой точки В режущей кромки зуба рейки:

x¢_B = -h_a0 × tga; y¢_B = -h_a0, где h_a0 = h^*_a × m.

Если подставить эти выражения в (1.48) для х и у, то получим уравнения искомой переходной кривой профиля:

xB = -(ha0 tga + rj)cos(j - y) + (-ha0 + r)sin(j -y); yB = -(ha0 tga + rj)sin(j - y) + (-ha0 - r)cos(j -y)-rf.

(1.49)

Пределы изменения угла j определяют из следующих соображений. При отсутствии подрезания эвольвентная и переходная части профиля имеют плавное сопряжение в точке 3 (рис. 8), т.е. в этой точке у них имеется общая нормаль. Вершина В зуба рейки (см. рис. 7) касается эвольвентной части профиля зуба колеса в том положении обкатываемой рейки, когда точка М нормали к вершине В режущей кромки ВС рейки окажется лежащей на делительной окружности нарезаемого колеса. Основываясь на этом, имеем

Начальная точка I (см. рис. 5) переходной части профиля принадлежит одновременно и окружности впадин, причем в этой точке окружность впадин и переходная часть профиля имеют общую нормаль. Вершина В зуба рейки (см. рис. 7) касается в точке I окружности впадин в том положении обкатываемого инструмента, когда точка нормали к режущей кромке ВD ока­зывается на делительной окружности нарезаемого колеса. Осно­вываясь на этом, имеем

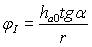
Рассмотрим теперь случай, когда рейка имеет закругления на вершинах. Произвольная точка 3 (см. рис. 8) закругления коснется переходной части профиля зуба колеса при таком положении обкатываемого инструмента, когда точка K нормали KЗ к закруглению окажется на делительной окружности нарезаемого колеса, т.е. когда точка K станет полюсом зацепления.

Высота закругления С=с^* т (см. рис. 8), тогда радиус закругления r_f будет найден из условия

Вместе с тем h¢ = h_a0 – c^*m, h² = h_a0 – r_f. Координаты точки L – центра закругления:

xL¢ = -(h¢ tga + rf cosa); yL¢ = -h² =-(ha0 – rf ),

(1.50)

координаты произвольной точки 3 закругления,определяемой угловым параметром m:

x3¢ = xL¢ + rf cosm; y3¢ = yL¢ - rf sinm.

(1.51)

Связь между параметрами m и j выражается зависимостью (см. рис. 8)

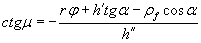
(1.52)

С учетом (1.48), (1.50) и (1.51) уравнение переходной кривой при наличии на зубьях рейки закруглений примет вид

x3 = -(h¢ tga + rf cosa - rf cosm +rj)cos(j - y) + (- h¢ - rf cosm + r)sin(j - y); y3 = (h¢ tga + rf cosa - rf cosm +rj)sin(j - y) + (- h¢ - rf sinm + r)cos(j - y) – rf.

(1.53)

Пределы изменения угла j определяют из следующих соображений. В точке I (см. рис. 5) касания переходной части профиля с окружностью впадин угол m = 90°, отсюда следует, что

В точке II касания переходной и эвольвентной частей профиля угол m = a, откуда следует

Выведенныеформулы справедливы идля случая нарезания колес червячной фрезой.

 

 

 

57-60

Глава 2. ПРОЕКТИРОВАНИЕ ПЛАНЕТАРНЫХ ЗУБЧАТЫХ МЕХАНИЗМОВ С ЦИЛИНДРИЧЕСКИМИ КОЛЕСАМИ

 

Извсех видов механических передач планетарные зубчатые передачи более других снижают материалоемкость машины. Эти механизмы по сравнению с зубчатыми передачами, имеющими неподвижные оси вращения, обладают меньшими габаритными размерами и массой при равных передаточных отношениях. Однако задача проектирования планетарных передач является более трудоемкой и объемной по времени, чем проектирование обычных передач. В этих механизмах числа зубьев колес должны удовлетворять совокупности многих условий и ограничений. При этом число расчетных уравнений бывает меньше числа неизвестных, поэтому нельзя получить однозначного решения. Таким образом, задача определения чисел зубьев колес сводится к поиску множества вариантов, соответствующих исходным данным, и выбору оптимального.

Решение задач по синтезу планетарных передач можно значительно ускорить, используя ЭВМ. Эту задачу решают применительно к наиболее распространенным схемам соосных планетарных механизмов, составленных из передач без смещения, одного модуля и включающих два и более двухвенцовых сателлита.

 

 

§ 1. Основные характеристики планетарных механизмов

 

В табл. 3 представлены характеристики наиболее распространенных планетарных механизмов 2К-Н по классификации, приведенной в работе [4]. Значения рациональных передаточных отношений, в зависимости от выбранного входного звена механизма, для каждой схемы находятся в некотором ограниченном диапазоне. Когда передаточное отношение выходит за пределы этого диапазона, проектируемый привод выполняют в виде последовательного соединения рассматриваемых планетарных механизмов или комбинации рядовой передачи и планетарного механизма. Так образуются двух- и трехступенчатые механизмы.

Наиболее часто в силовых приводах применяют однорядный планетарный механизм с одновенцовыми сателлитами (рис. 9, а). Эго объясняется сравнительной простотой его изготовления, малыми осевыми габаритами, высоким КПД, а также простотой подбора чисел зубьев колес. При реализации больших передаточных отношений последовательно соединяют несколько однорядных планетарных механизмов.

Несколько больший диапазон передаточных отношений имеет планетарный механизм, выполненный по схеме, представленной на рис. 9, 6 (см. табл. 3). Он также применяется в силовых приводах и имеет высокий КПД. Однако наличие двухвенцового сателлита усложняет подбор чисел зубьев колес и увеличивает число сателлитов. Поэтому конструкторы редко применяют такую схему механизма.

Широкие кинематические возможности имеют схемы, изображенные на рис. 9, в и г (см. табл. 3), Передаточные отношения в этих схемах планетарных механизмов могуг быть положительными к отрицательными, абсолютное значение изменяется в широком диапазоне. Однако с увеличением передаточного отношения КПД передач резко падает. При входном колесе z₁ не рекомендуется назначать U > 25, так как при этом возрастают потери на трение и появляется опасность возникновения самоторможения. Поэтому в подобных механизмах за входное звено принимают водило. Эти схемы применяются в несиловых установках кратковременного действия и приводах приборов, когда необходимо редуцировать очень большое или малое передаточное отношение и КПД механизма не имеет решающего значения. Преимущество при этом отдается схеме на рис. 9, г (см. табл. 3) с двумя внутренними зацеплениями, как более компактной и имеющей несколько больший КПД.

 

 

§ 2. Общие условия синтеза планетарных механизмов

 

При кинематическом синтезе многосателлитной планетарной передачи, конструируемой по заданной схеме, решают задачи подбора таких чисел зубьев ее колес, которые будут удовлетворять условиям: выполнения заданного передаточного отношения, правильности зацепления зубьев колес, соосности входного и выходного валов, соседства и сборки.

Первые три условия являются общими при синтезе любой планетарной зубчатой передачи. Остальные диктуются особенностями кинематических схем планетарных механизмов.

При синтезе планетарного механизма необходимо учитывать основные механические показатели качества: 1) КПД; 2) минимальные габаритные размеры; 3) массу проектируемого механизма;

4) динамические нагрузки в зацеплениях колес механизма, которые снижаются при выполнении следующих требований: а) числа зубьев центральных колес и числа сателлитов должны быть взаимно простыми; б) числа зубьев сопряженных колес не должны иметь общих множителей [4].

При проектировании планетарного механизма силового привода необходимо оценивать его КПД до подбора чисел зубьев. В учебной практике можно воспользоваться рекомендациями табл. 3 или аналитическими зависимостями, приведенными в работе [4, с.79].

Требования к габаритным размерам планетарного механизма обычно сводятся к тому, чтобы они не превышали заданных.

Масса механизма зависит от многих факторов, однако в данном пособии учитывается только один из них; сумма чисел зубьев S всех колес механизма. Эту характеристику в дальнейшем и будем принимать за критерий оценки массы.

Предположим, что схема механизма с учетом КПД выбрана, передаточное отношение и число сателлитов заданы. Все колеса имеют одинаковый модуль, который либо задан в исходных данных, либо может быть определен по формуле

(2.1)

где M₁ - крутящий момент на входном звене; z₁ - число зубьев центрального колеса; k - число сателлитов планетарного механизма.

В этом случае проектирование сводится к подбору чисел зубьев колес. При решении этой задачи требуется учитывать следующие условия.

1. Сочетанием чисел зубьев колес должно с допустимой точностью обеспечиваться заданное передаточное отношение. При этом числа зубьев колес должны быть целыми числами.

2. При отсутствии специальных требований к габаритным размерам желательно использовать в планетарном механизме зубчатые колеса без смещений.

Этими ограничениями учитывается отсутствие заклинивания передачи и подрезания зубьев: для колес с внешними зубьями, нарезанных стандартным инструментом, z ³ z_min = 17, для колес с внутренними зубьями в зависимости от параметров долбяка принимают z > z_min = 85 при h^*_a = 1 и z ³ z_min = 58 при h^*_а = 0,8.

3. Условием соосности определяется соосное расположение центральных колес планетарного механизма с водилом H. Соосность основных звеньев приводит к равенству межосевых расстояний зацепляющихся колес. Для механизмов, изображенных на рис, 9, условие соосности можно конкретизировать в виде соотношений между радиусом водила и размерами радиусов начальных окружностей:

схема а: rH = rW1 + rW2 = rW3 – rW2; схема б: rH = rW1 + rW2 = rW4 – rW3; схема в: rH = rW1 + rW2 = rW3 + rW4; схема г: rH = rW1 – rW2 = rW4 – rW3.

(2.2)

4. Условие совместности, или соседства, которое учитывает возможность свободного размещения сателлитов без соприкосновения их друг с другом. Это условие будет выполнено, если расстояние между осями сателлитов будет больше диаметра окружности вершин наибольшего сателлита d_a2,3. Математически это условие для механизмов, представленных на рис. 9, выражается неравенством

(2.3)

В числителе правой часта неравенства (2.3) выбирают z₂ в том случае, если z₂ > z₃ , и наоборот, если z₂ < z₃, то выбирают z_3. В знаменателе ставят относительное межосевое расстояние, т.е. если зацепление внешнее, то сумму чисел зубьев, если зацепление внутреннее - то разность чисел зубьев колес.

Если необходимо определить наибольшее число сателлитов, которое может иметь планетарный механизм с известными числами зубьев, условие соседства приводят к виду

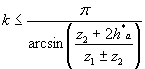
(2.4)

5. Условие сборки с симметрией зон зацепления выражается соотношением

(2.5)

где k - число сателлитов; Р = 0, 1, 2, 3... - целое число; Ц - любое целое число.

Выполнение этого равенства фактически означает следующее: если один из сателлитов свободно устанавливается на вертикальной оси (рис. 10), то все последующие сателлиты будут свободно входить в зацепление с соответствующими колесами в той же позиции. Для этого необходимо повернуть водило на угол

(2.6)

У двухвенцовых сателлитов зубья одного венца одинаково ориентированы относительно зубьев второго венца.

 

 

§ 3. Методика синтеза отдельных схем планетарных механизмов

 

В исходных данных курсового проекта числа зубьев колес не заданы, и их необходимо определить на стадии проектирования кинематической схемы. Задача определения чисел зубьев сводится к составлению исходных уравнений, отражающих указанные условия и требования для каждой рассматриваемой схемы, и их совместному решению. Одним из простых методов определения чисел зубьев является метод сомножителей, при котором числа зубьев колес планетарного механизма определяют для заданного передаточного отношения, при правильном зацеплении зубьев колес (отсутствие подрезания зубьев и заклинивания передачи) и выполнении условия соосности. При этом проверяют условия сборки, соседства и учитывают конструктивные ограничения.

Планетарный двухрядный механизм со смешанным зацеплением (рис. 9, б). Дано: U₁⁽⁴⁾_H, k и m. Перепишем все ранее выведенные формулы и условия синтеза:

уравнение передаточного отношения

(2.7)

уравнение соосности

a_W = r_W1 + r_W2 = r_W4 - r_W3

или при равных модулях во всех зацеплениях механизма

z1 + z2 = z4 – z3

(2.8)

Уравнение (2.5) сборки имеет вид

Условие (2.3) совместности при z₂ > z₃ имеет вид

в случае, если z₃ > z₂,

Решение проводят методом сомножителей. Из уравнения (2.7) передаточного отношения определяют числовое значение (z₂z₄)/(z₁z₃) и полученное число раскладывают на сомножители А, В, С и D которым числа зубьев z₁, z₂, z₃, z₄ должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма a_W1=a_W2, вводят дополнительные множители, поставленные в скобки:

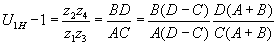
С учетом условия соосности для этой схемы

z₁ = A(D - C)q;

z₂ = B(D - C)q;

z₃ = C(A + B)q;

z₄ = D(A + B)q.

Общий множитель q подбирают так, чтобы все числа зубьев были целыми и z₁ > 17; z₂ > 17; z₃ ³ 20; z₄ ³ 85, а z₄ – z₃ ³ 8.

Затем следует проверить, как выполняются условия сборки (2.5), соседства (условие (2.3)) и требования к габаритным размерам.

 

Планетарные двухрядные механизмы с двумя внешними (рис. 9, г) или двумя внутренними (рис. 9, в) зацеплениями. Для указанных схем плане-тарных механизмов ведущим звеном является водило U_1H = w_H / w₁. При решении задачи полагают заданными U_1H, k и т.

Выписывают необходимые уравнения:

уравнение передаточного отношения

(2.10)

уравнение соосности

rW1 ± rW2 = rW3 ± rW4 или z1 ± z2 = z4 ± z3

(2.11)

(знак плюс соответствует внешнему зацеплению, знак (минус) соответствует внутреннему зацеплению);

уравнение сборки

условие соседства

Решение проводят методом сомножителей.

Из уравнения (2.10) определяют числовое значение отношения, которое заменяют отношением, составленным из сомножителей А, B, C и D, соответственно пропорциональных числам зубьев: BD/AC=(1 – 1/U_H1).

Чтобы обеспечить соосность двухрядного планетарного механизма (a_WI = a_WII), числа зубьев подсчитывают по формулам

z1 = A(D ± C)q; z2 = B(D ± C)q; z3 = C(A ± B)q; z4 = D(A ± B)q.

(2.12)

Последним этапом решения задачи синтеза является проверка по условиям сборки и соседства.

 

Однорядный планетарный механизм (рис. 9, а). Дано: U_1H, k и т. Выписывают все необходимые уравнения:

уравнение передаточного отношения

(2.13)

уравнение соосности для заданной схемы механизма r_W1 + 2r_W2 = r_W3. Если зубья колес планетарного механизма без смещений, то z₁ + 2z₂ = z₃;

уравнение сборки

(2.14)

условие соседства имеет вид

Далее решение проводят в такой последовательности:

1. Задают число зубьев центрального колеса z₁ > z_min = 17.

2. Из уравнения (2.13) определяют z₃ = z₁(U_1H - 1). Число зубьев опорного колеса z₃ должно быть целым числом, большим 85.

3. Из уравнения соосности (2.14) определяют z₂ = (z₃ – z₁)/2

Число эубьев у сателлита должно быть целым числом, большим или равным 20.

4. Проверяют условие сборки по уравнению (2.5):

5. Проверяют условие соседства по неравенству (2.3):

Если хотя бы одно из условий не выполняется, то следует выбрать другое значение x₁.

После определения чисел зубьев планетарного механизма и расчета радиусов делительных окружностей колес на листе изображают кинематическую схему механизма в двух проекциях и на одной из них строят треугольники скоростей (см. рис. 3, б). Угловые скорости колеса z₁ и водила Н пропорциональны тангенсам углов y₁ и y₂; передаточное отношение U_1H =w₁/w_H = tgy / tgy_H = AA¢/AA² Углы y₁ и y₂ однозначны, следовательно, и угловые скорости будут иметь одинаковое направление.

 

 

§ 4. Критерии оптимальности планетарного механизма

 

При синтезе планетарного механизма необходимо учитывал не только условия, определяющие его кинематику, но и дополнительные требования, позволяющие улучшить качество механизма. Условия кинематической работоспособности механизма рассмотрены в предыдущих параграфах. Соответствующие им решения многовариантны, поэтому в конце вычислительного процесса из них выбирают оптимальное. Таковых может быть несколько, в зависимости от числа оценочных параметров. В качестве критериев оптимальности планетарного механизма принимают (см. рис. 9):

1. наибольший радиальный габарит Г₁, или Г₂: Г₁, если Г₁ > Г₂; если Г₂ > Г₁;

2. сумму чисел зубьев S = z₁+z₂+z₃+z₄, косвенно опреде­ляющую массу и трудоемкость изготовления;

3. условие отсутствия кратности числу сателлитов k числа зубьев центральных колес.

Для поиска оптимальных решений у всех вариантов набора z₁,z₂,z₃,z₄ и k, удовлетворяющих кинематическим условиям, рассчитывают оценочные показатели S, Г₁, Г₂. Затем, последовательно сравнивая между собой величины S_i, находят наименьший критерий S_min. Затем соответствующий ему набор значений S_min, z₁, z₂, z₃ и k принимают за параметры оптимального механизма, имеющего наименьшую массу и трудоемкость изготовления колес механизма при прочих равных условиях. Аналогично, сравнивая размеры Г₁, если Г₁ > Г₂ или Г₂, если Г₂ > Г₁, находят наименьший показатель Г_min. Соответствующий ему набор параметров, Г_min, S, z₁, z₂, z₃, z₄ и k выделяют в оптимальный вариант механизма с наилучшим радиальным габаритом при прочих равных условиях.

Во всех решениях, удовлетворяющих кинематическим требованиям, проверяют кратность числа зубьев z₁, а затем z₄ - числу сателлитов k. Наборы Г, S, z₁, z₂, z₃, z₄ и k, не отвечающие этому условию, принимают за параметры оптимальных механизмов, наиболее динамически работоспособных при прочих равных условиях.

 

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: