 |
Передаточная функция и частотные характеристики программы интегрирования, реализованная на ЦВМ методом Эйлера.
|
|
|
|
Реализация программного интегрирования методом Эйлера: Рекуррентная формула выходного сигнала:
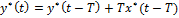
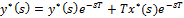
Передаточная функция программы интегрирования:
СММ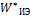 
:
| T |
|
Рассмотрим частотные характеристики:
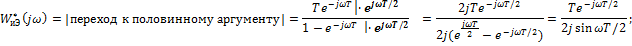
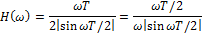
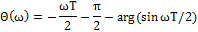
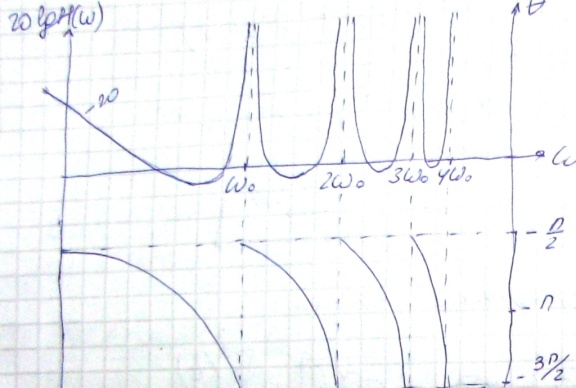
Рассмотрим ЛАФЧХ системы:
При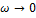 
: 
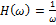, значит в области низких частот ЛАФЧХ такая же, как и у идеального интегратора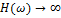 
;
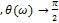Однако далее на частотах, примерно больших 
, характеристика не совпадает с характеристикой идеального дифференциатора, как по амплитуде, так и по сдвигу фаз.
При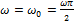 
: ;
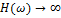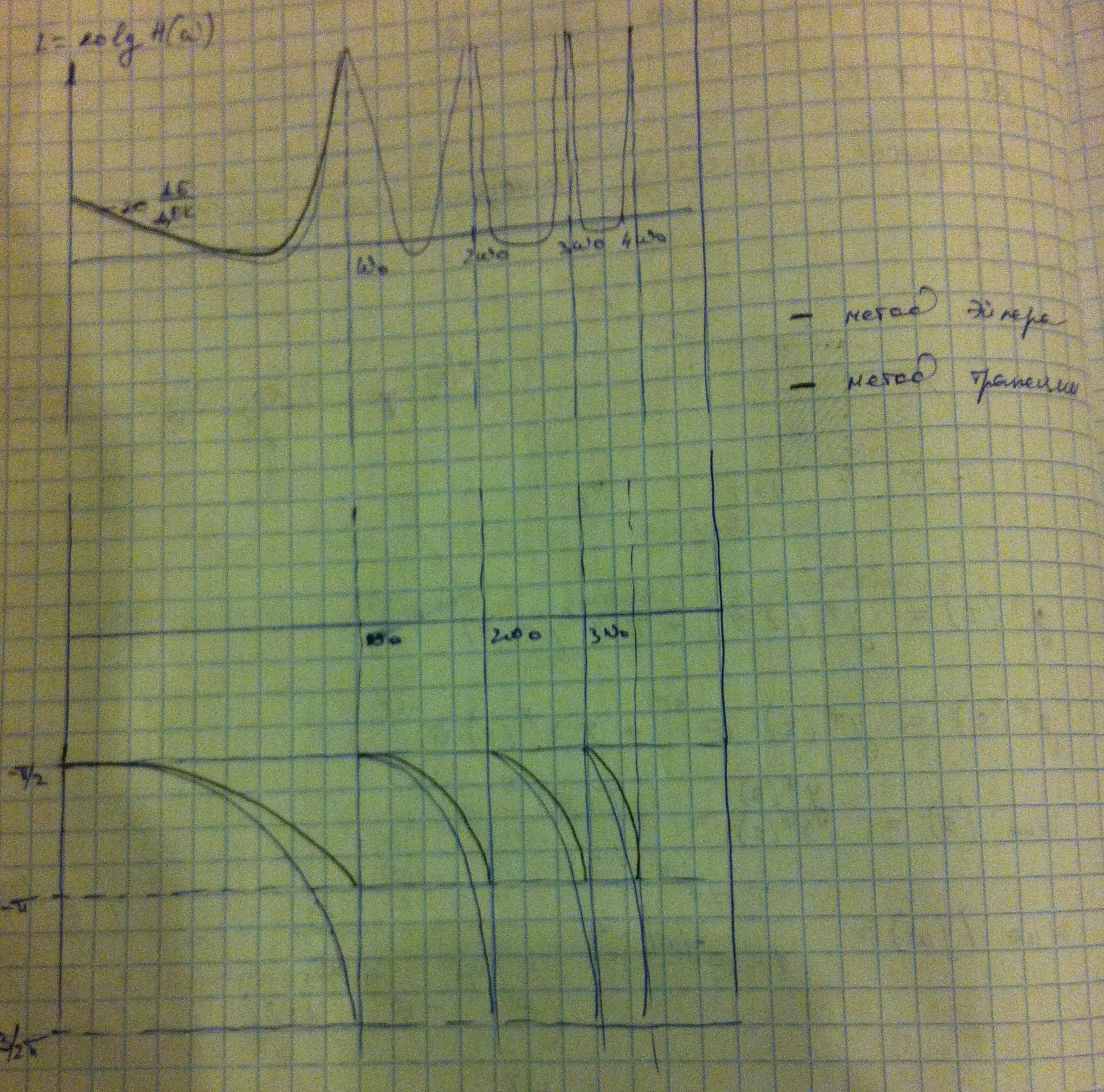
Передаточная функция и частотные характеристики программы интегрирования, реализованная на ЦВМ по методу трапеций.
y*(t)=y*(t-T) + Tx*(t-T) + (T2/2)x*(t-T)= y*(t-T) + Tx*(t-T) + (T/2)[x*(t-T) – x*(t-2T)]=
=[ 
] = y*(t-T) + (3/2)Tx*(t-T) – (1/2)Tx*(t-2T), y*(s)=y*(s)e(-sT) + (3/2)Tx*(s) e(-sT) – (1/2)Tx*(s) e(-2sT)
Передаточная функция: 
Амплитудная характеристика:
Частотная характеристика:
Передаточная функция и частотные характеристики программы дифференцирования.
=[переход к половинному аргументу]= 
при 
Передаточная функция и частотные характеристики программы реализации апериодического звена по методу Эйлера.
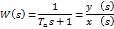
Соответствующее диффер. уравнение: 
Воспользуемся методом Эйлера: y*(t)=y*(t-T) + (T/Ta)(-y*(t-T) + x*(t-T))
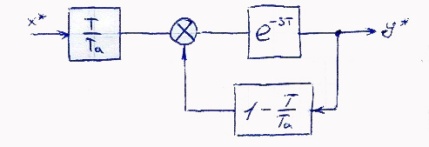
Передаточная функция имеет вид:
Структурная схема:
37. Передаточные функции дискретно-непрерывных систем на плоскости W*(s).
y(t)- непрерывный сигнал
y(s)= 
*(s)·W(s);
преобразование Лапласа дискретного входного сигнала. Будем рассматривать непрерывный выходной сигнал только в тактовые моменты времени, это означает, что мы вводим фиктивный ключ, который замыкается одновременно с первым.
Б)
Теперь рассмотрим дискретно-непрерывную систему: 
. Опять вводим фиктивный ключ
|
|
|
В)
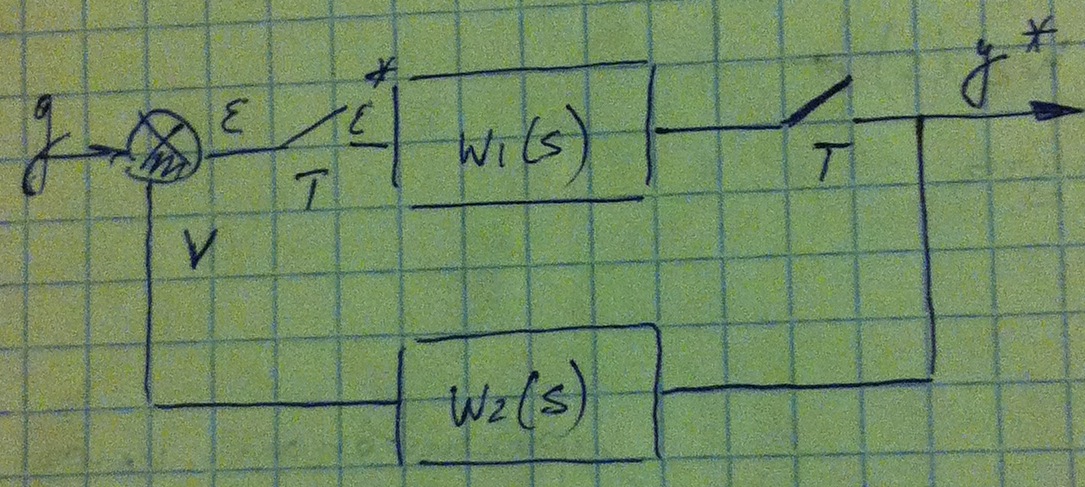
38. Исследование устойчивости дискретно-непрерывных систем на плоскости s и W*(s).
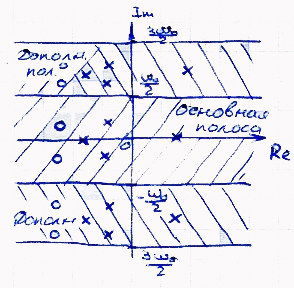
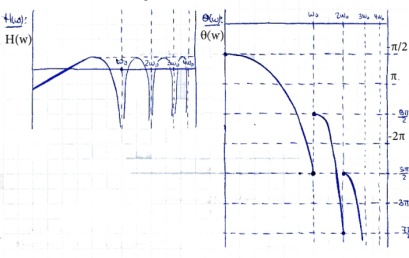При построении годографа возникает особенность: известно, что функция W*(jω) является периодической с периодом 2π/Т, а значит годограф при построении от 0 до бесконечности будет повторяться, поэтому нужно рассматривать годограф на отрезке (0;ω0), но лучше (-ω0/2; ω0/2). Можно построить годограф для положительной оси, а затем отобразить относительно действительной оси. Точно поострить годограф из-за бесконечного числа слагаемых нельзя, поэтому ограничиваются теми, которые дают наибольший вклад. n=0;-1;1 и т.д. Для исследования устойчивости дискретных систем применим критерий Найквиста. Допустим, что разомкнутая дискретная система устойчива, для того, чтобы замкнутая дискретная система была тоже устойчива, годограф не должен охватывать -1. Существенный недостаток состоит в поведении годографа вблизи границы устойчивости,т.к. отброшенные слагаемые могут повлиять на годограф.
Плоскость s: У передаточной функции разомкнутой системы есть особенность: нули и полюса в силу периодических свойств все те же нули и полюса будут и во всех доп. полосах, критерыий Найквиста работает на участке от 0 до ω0/2. Значит, рассматриваем те нули и полюса, которые попали в основную полосу справа. Допустим, полюс один, тогда для устойчивости замкнутой дискретной системы нужно, чтобы годограф при изменении Ω от 0 до ω0/2 охватил -1 в положительном направлении полраза.
Математический аппарат z-преобразования.
При переходе от s к z виду исчезает многозначность и удается избавиться от периодических свойств. Переход осуществляется заменой: 
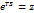(для дискретных сигналов только)
з 
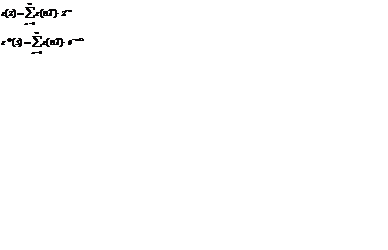
Свойства z – преобразований:
1. Линейность
з{ax(t) + by(t)}=ax(z) +by(z)
2. Сдвиг во времени
з{x(t-kT)}=z-kx(z)
3. Свойство частной производной
з 
4. з 
5. 
- это формула справедлива лишь тогда, когда ты знаешь, что этот предел существует
|
|
|
6.Наименьшее значение
|
|
|
