 |
Билинейное преобразование. Понятие псевдочастотных характеристик.
|
|
|
|
К билинейному преобразованию переходим путем замены переменных в z-форме для передаточной функции дискретной системы.
в результате замены приходим к 
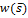
выразим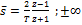 
пл-ти S выражается нулем плоскости z, подставляем 0 в 
получаем 
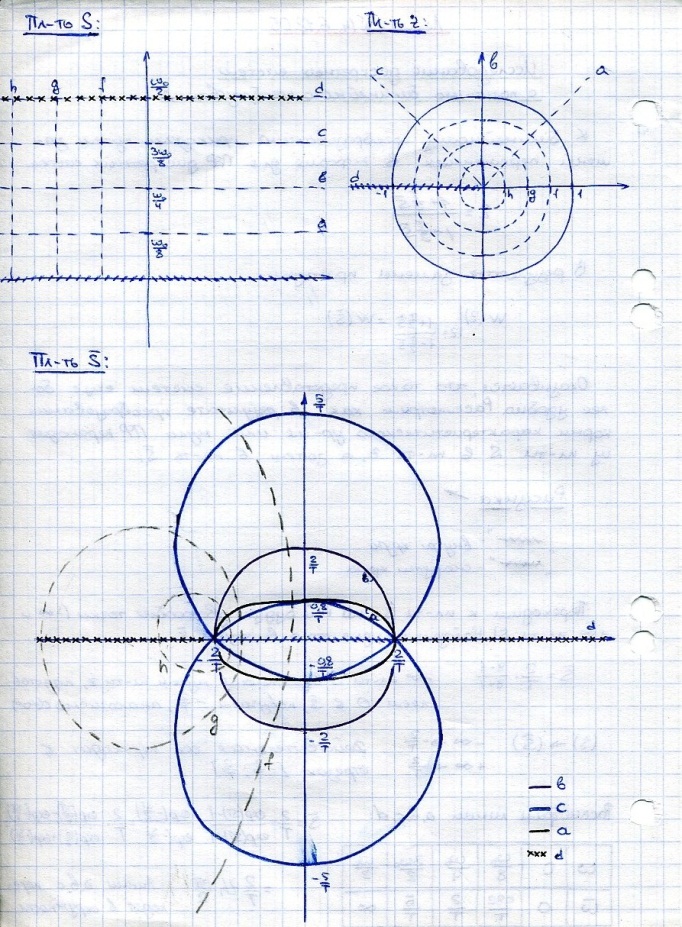
Действительная ось переходит в отрезок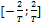 
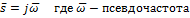
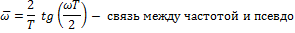
рассмотрим линии a b c d, они переходят в окружности.
| a | b | c | d | ||
| 
| 
| 
| 
| |
| 
| g w:val="EN-US"/></w:rPr><m:t>2</m:t></m:r></m:num><m:den><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/><w:lang w:val="EN-US"/></w:rPr><m:t>T</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="002B6683"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
| 
| 
|
Можно сделать вывод, что отрезок от 0 до 
перешел во всю положительную часть мнимой оси.
Рассмотрим вертикальные линии f, g, h. Эти линии тоже переходят в окружности. Центр окружности f лежит за точкой . Те же окружности можно нарисовать справа потому что верт линии с правой стороны дадут ту жу картину.
45. Передаточные функции дискретно-непрерывных систем с экстраполятором нулевого порядка на плоскости W(̄s̄).
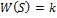- усилительное звено.
.
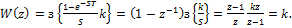
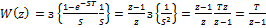
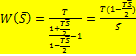
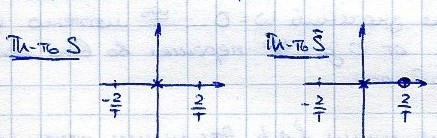
где a – постоянная времени апериодического звена.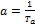 
При переходе из 
в 
коэффициент усиления остается постоянным.
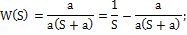
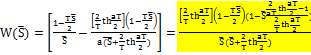
Вычисление переходного процесса в дискретные моменты времени с помощью вычетов.
Преобразование Лапласа для непрерывной системы: прямое 
и обратное 
, где C – абсцисса абсолютной сходимости интеграла (все особенности y(s) лежат слева). Рассматриваем систему только в дискретные моменты времени 
:
. Поскольку для дискретных систем плоскость S делится на основную и дополнительные полосы, можно записать интеграл как сумму по полосам. Сделаем замену 
: 
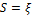. Меняем местами сумму и интеграл и делаем замену 
: 
|
|
|
= 
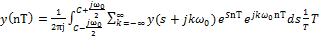
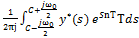. Применим z-преобразование: 
. Получим: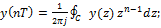 
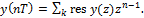Решение: 
.
Вычисление переходного процесса в дискретные моменты времени с помощью разложения сигнала Y(z) в степенной ряд.
Данный метод основан на работе с изображением выходного сигнала y(z) и базируется на определении z-преобразования: 
. Нужно разложить в степенной ряд по степеням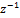 
и коэффициенты перед z будут давать нужные значения в тактовые моменты времени: 
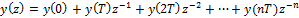. Запишем сигнал во временной области: 
.
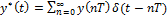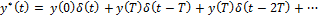
Один из способов разложения степенного ряда – деление многочлена на многочлен: 
.
Вычисление переходного процесса в дискретные моменты времени с помощью разложения сигнала Y(z)/z на простые дроби.
Данный метод работает с изображением y(z), но основан на разбиении y(z)/z на простые дроби. Тогда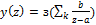 
, чему соответствует 
– сумма временных функций. Полученное таким образом выражение для y(t) в виде суммы временных функций дает правильный результат только для 
: 
. Мы рассматривали систему только в дискретные моменты времени, поэтому 
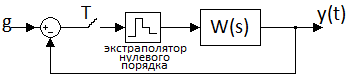
. А для исследования системы в межтактные моменты времени существует модифицированное z-преобразование: y(z,m), где m - доля между тактами, причем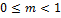 
. Пример: перед непрерывной системой ставится ключ с T и экстраполятор нулевого порядка. Считается передаточная функция от всей системы (учитывая наши введенные элементы), ищется выходной сигнал, который должен совпасть (с учетом ) с выходным сигналом просто системы (без введенных нами элементов).
|
|
|
