Отличие применяемых методов измерений магнитным ВИП и ультразвуковым ВИП

 

Сравнение возможностей ультразвукового и магнитного дефектоскопов по обнаружению особенностей по обнаружению особенностей трубопровода приведено в таблице № 8.

Таблица № 8

Наименование особенности	Обнаружение ультразвуковым ВИП	Обнаружение магнитным ВИП
Нарушение геометрии трубы:
Вмятина	+	+*
Гофра	+	+*
Овальность	-	-
Внутристенные дефекты:
Расслоение	+	-
Расслоение поверхнос.	+	+
Наклонное расслоение	+	-
Расслоение, ПСШ	+	-
Включение	+	-
Потери металла (внешние и внутренние):
«Питинговая коррозия»	+	+
Общая коррозия	+	+
Потери металла на вмятинах, гофрах	+	+
Риска вдоль трубы	+	-
Риска наклонная	+	+
Дефекты сварных швов:
Поперечные швы	-	+
Продолные швы	-	-
Особенности, связанные с ремонтом трубопровода:
Приварная муфта	+	+
Не приварная муфта	-	+
Заплата	+	+
Трубная арматура:
Задвижка	+	+
Тройник (отвод)	+	+
Вантуз	+	+
Сварное присоединение	+	+
Кожух	-	+

 

* - особенность может быть не обнаружена в районе поперечного сварного шва или если она имеет гладкий профиль.

 

Изучение основных элементов виброизмерительной аппаратуры и измерение вибрации роторных машин

 

 

Колебания машин.

1.1. Введение в колебания и вибрацию машин и механизмов.

Вибрация – это колебания относительно неподвижной точки. Это результат динамических сил, проистекающих в машинах, которые имеют подвижные части. Различные части машины вибрируют на разных частотах и с различной амплитудой. Вибрация, как правило, вызывает износ и усталость механизмов, и зачастую, влияет на полный вывод механизма из работоспособного состояния.

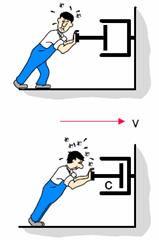
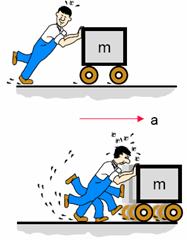
1.2. Механические параметры и компоненты вибрации.

Перемещение	Скорость	Ускорение
F=k×d	F=c×v	F=m×v

1.3. Простейшие формы вибрации систем.

Из рисунка 1.1 видно, что колебания простейшей системы, состоящей из массы и упругого элемента можно описать синусоидальной диаграммы с амплитудой (D) и периодом (T). Частота колебаний (f) определяется как величина обратно пропорциональная периоду. Произведение частоты на 2p дает нам угловую частоту пропорциональную корню отношения коэффициента пружины и массы, которая является собственной частотой данной системы.

В общем случае перемещение может быть описано как , где d – мгновенное значение, D – пиковое значение.

 

 

Рисунок 1.1. Колебания простейшей системы.

1.4. Колебания без демпфирования.

 

На рисунке 1.2. изображено колебание одномассовой системы без демпфирования (затухания). Как видно из рисунка при достижении максимума перемещения кинетическая энергия равна нулю, соответственно потенциальная энергия (скорость) имеет максимальное значение и равна . В среднем положении потенциальная энергия равна нулю, при этом кинетическая достигает максимального значения .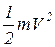

Для гармонических колебаний перемещения можно записать следующее

 

.

 

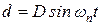С помощью дифференцирования мы можем определить скорость

 

,

 

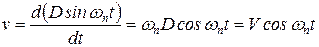где V – пиковое значение скорости, и определяется как .

Используя закон сохранения энергии мы можем получить собственную частоту колебаний системы

 

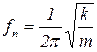
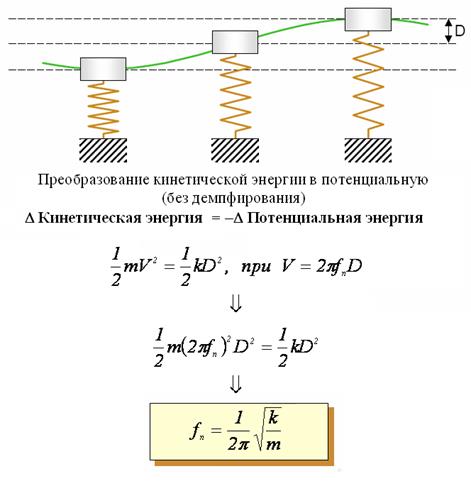
Рисунок 1.2. Колебания одномассовой системы без демпфирования.

 

На рисунке 1.3. изображено изменение колебаний одномассовой системы при увеличении массы. Как видно из рисунка увеличение массы приводит к уменьшению частоты и увеличению периода колебаний.

Рисунок 1.3. Колебания одномассовой системы при увеличении массы.

1.5. Колебания с демпфированием.

На рисунке 1.5. проиллюстрировано изменение колебаний одномассовой системы с демпфирующим элементом. Результатом демпфирования является снижение амплитуды колебаний во времени.

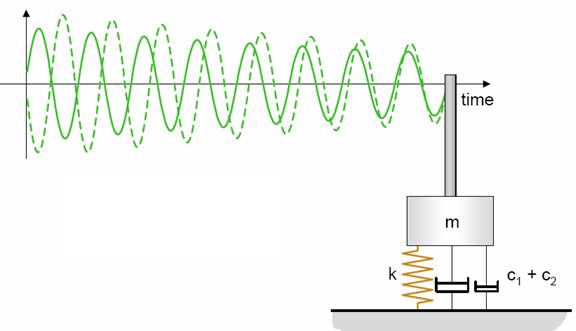
Рисунок 1.4. Колебания одномассовой системы с демпфирующим элементом.

1.6. Вынужденные колебания.

При приложении внешних сил (F) на систему, система начинает колебаться и выходить из состояния равновесия и колеблется с частотой, которую имеет внешняя сила. Но это не означает что система будет колебаться с такой же амплитудой и углом (фазой) (рисунок 1.5.а).

Как видно из рисунка в случае совпадения собственной частоты и частоты возбуждающей силы, в отсутствие демпфера может произойти явление резонанса (рисунок 1.5.б).

При увеличении частоты возмущающей силы изменяется угол (фаза) колебаний системы, а также и амплитуда колебаний (рисунок 1.5.в).

 

Рисунок 1.5. Вынужденные колебания.

Принимая во внимание, что реальные механические системы имеют более сложное строение, рассмотрим колебания системы, состоящей из двух простейших систем (рисунок 1.6.)

Как видно из рисунка система состоит из двух простейших систем. При воздействии внешней периодической силы обе системы начинают колебаться на собственных частотах, отличие заключается в том, что верхняя система колеблется не только относительно внешней приложенной силы, но и от воздействия на нее нижней системы. Т.е. как видно из рисунка на амплитудно ‑ частотной характеристике имеется два пиковых значения.

 

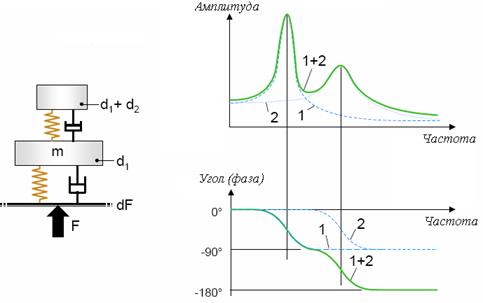
Рисунок 1.6. Колебания системы из двух простейших систем.

 

На рисунке 1.7 изображены система с одной и множеством степенями свободы.

Система с одной степенью свободы - система, которая может выполнять движение только в одном направлении.

В случае сложных систем движение может осуществляться во многих направлениях. В данных системах мы имеем возможность наблюдать за каждым пиком от степени свободы в амплитудно – частотной характеристике.

 

Рисунок 1.7. Колебания системы с множеством степенями свободы.

 

На практике же в большинстве случаев чрезвычайно сложно разделить различные механические компоненты. Это связано с тем, что каждая реальная механическая система, даже самая простейшая имеет в своем составе множество простейших систем и зачастую достаточно сложно разделить их частотные компоненты. Это можно рассмотреть на примере упрощенной схемы электродвигателя (рисунок 1.8).

 

Рисунок 1.8. Упрощенная схема электродвигателя.

 

1.7. Вынужденные колебания и вибрация.

 

В реальных системах частотные характеристики являются трудно распознаваемыми, это связано с конструктивными особенностями таких систем. На рисунке 1.9 изображено влияние основных параметров системы на вибрационное состояние системы и это только для электродвигателя.

 

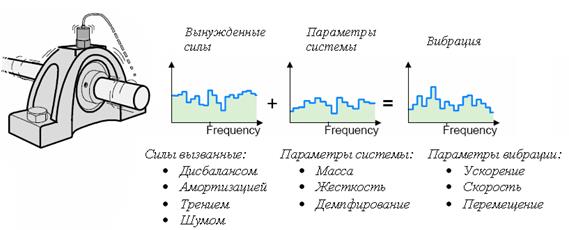
Рисунок 1.9.

1.8. Типы сигналов.

 

Первоначально сигналы можно разделить на две большие группы детерминированные и случайные (рисунок 1.10).

Детерминированные сигналы это сигналы, значения которых в любой момент времени или в произвольной точке пространства (а равно и в зависимости от любых других аргументов) являются заранее известными или могут быть достаточно точно определены (вычислены).

К периодическим относят гармонические и полигармонические сигналы.

К периодическим относят гармонические и полигармонические сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3,... - любое целое число, Т - период, являющийся конечным отрезком времени (рисунок 1.11).

Гармонические сигналы (или синусоидальные), описываются следующими формулами:

s(t) = A×sin(2pf_оt+f) = A×sin(w_оt+f),

или:

s(t) = A×cos(w_оt+j),

где А, f_o, w_o, j, f - постоянные величины: А - амплитуда сигнала, f_о - циклическая частота в герцах, w_о = 2pf_о - угловая частота в радианах, j и f - начальные фазовые углы в радианах. Период одного колебания T = 1/f_о = 2p/w_o. При j = f-p/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты f_о (при t = 0).

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:

 

s(t) = A_nsin(w_nt+j_n),

или непосредственно функцией s(t) = y(t ± kT_p), k = 1,2,3,..., где Т_p - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение f_p =1/T_p называют фундаментальной частотой колебаний. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (f_о = 0) и произвольного (в пределе - бесконечного) числа гармонических составляющих с частотами, кратными фундаментальной частоте f_p, и с произвольными значениями амплитуд A_n и фаз j_n. Другими словами, частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).

 

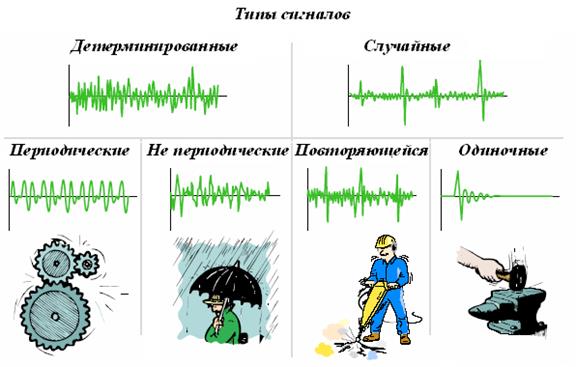
Рисунок 1.10. Типы сигналов.

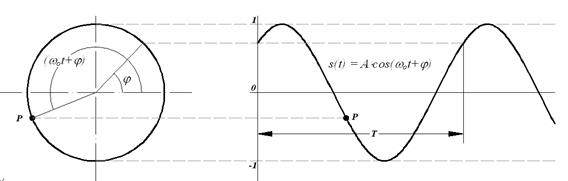
Рисунок 1.11. Периодический сигнал.

К непериодическим сигналам относят почти периодические и апериодические или переходные сигналы (рисунок 1.12).

 

Рисунок 1.12. Почти периодический сигнал и спектр его амплитуд.

 

Почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов, но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рисунке 1.13 показан пример апериодического сигнала, заданного формулой на интервале (0, ¥):

s(t) = exp(-a×t) - exp(-b×t),

где a и b – константы, в данном случае a = 0.15, b = 0.17. Частотный спектр апериодических сигналов непрерывен. Для их представления в частотной области используется интегральное преобразование Фурье, которым отображается спектральная плотность сигнала.

 

Рисунок 1.13. Апериодический сигнал и модуль его спектра.

 

К апериодическим сигналам относятся также импульсные сигналы, которые в радиотехнике и в отраслях, широко ее использующих, часто рассматривают в виде отдельного класса сигналов. Импульсы представляют собой сигналы, как правило, определенной и достаточно простой формы, существующие в пределах конечных временных интервалов. Сигнал, приведенный на рисунок 1.14, относится к числу импульсных.

 

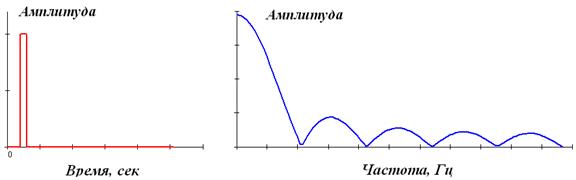
Рисунок. 1.14. Импульсный сигнал и модуль его спектра.

2. Основы вибродиагностики.

 

Диагностирование состояния машин и оценка степени опасности повреждения на основе данных контроля вибрации - один из наиболее эффективных методов повышения надежности оборудования.

Вибрационное диагностирование объектов проводится в три этапа: первичное описание вибрационного состояния объекта, выделение признаков и принятие решения.

На этапе поиска информативных признаков ограничивают число измеряемых параметров вибрации, шума и ударов. При этом из множества параметров, характеризующих вибрационный процесс, выделяют только те, которые прямо или косвенно характеризуют состояние объекта. По этим параметрам формируют информативную систему признаков, используемых при диагностировании.

Основные измеряемые параметры для определения состояния машин методами вибродиагностики, приведены в таблице 2.1.

 

Таблица №2.1. ‑ Основные измеряемые параметры.

Основные измеряемые параметры	Математическое описание	Обозначения
Виброперемещение	x(t)=X0sin(wt+j)	X0 -амплитуда виброперемещения
Виброскорость	v(t)=V0sin(wt+j)	V0=wX0
Виброускорение	a(t)=A0sin(wt+j)	A0=w2X0; w, j - круговая частота и фаза колебания соответственно

 

2.1. Количественная оценка амплитуд механических колебаний.

Для количественной оценки амплитуд механических колебаний, можно использовать разные значения, на рисунке 2.1 приведены: двойная амплитуда, пиковое значение, среднее значение и среднеквадратичного значения колебания синусоидальной формы.

Двойная амплитуда, отображающая полных размах колебаний. Является важным параметром, например, в случаях когда смещение механических колебаний детали машины является критическим с точки зрения максимально допустимых механических напряжений и зазоров.

 

Рисунок 2.1. – Количественная оценка амплитуд колебаний

Пиковое значение эффективно именно при оценке кратковременных механических ударов и т.д. Однако, пиковое значение отображает только максимальное значение исследуемых колебаний, и не заключает в себе их временное развитие.

Среднее значение (усредненное или абсолютное) отображает временное развитие исследуемых колебаний, но его практическое применение ограничено ввиду того, что оно не имеет непосредственной связи ни с коей физической величиной этих колебаний.

 

.

 

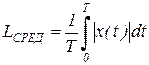Среднеквадратичное значение (СКЗ) является самым важным, так как в нем учитывается временное развитие исследуемых колебаний и оно непосредственно отображает значение, связанное с энергией и, следовательно, с разрушающей способностью этих колебаний. Отметим, что СКЗ синусоидальных колебаний равно умноженному на 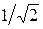пиковому значению этих колебаний.

 

.

 

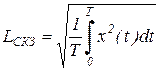2.2. Измерение колебаний машин.

2.2.1. Колебания машин.

При эксплуатации насосных агрегатов имеет место два принципиально различных метода измерения вибраций (колебаний) - при помощи датчиков измерения абсолютных колебаний и относительных колебаний. Колебания насосных агрегатов создаются преимущественно их вращающимися частями и пульсациями давления в насосе и подводящих трубопроводах. При этом, главным возбудителем колебаний является неуравновешенность роторов насоса и электродвигателя.

Ротор, имеющий дебаланс, создает во время вращения свободные центробежные силы, зависимые от частоты вращения (рисунок 2.2). Их величина вычисляется на основе следующего соотношения:

 

F = u × r × w2

(2.1)

 

где F - центробежная сила; u - дебаланс; r - радиус; w - частота вращения.

Вызванные дебалансом центробежные силы побуждают ротор и вал ротора к колебаниям. Через масляную пленку подшипников скольжения (или через подшипники качения) колебания и усилия передаются на опоры и на фундамент машины. Передаваемые колебания зависят от разных параметров. Самые существенные из них: жесткость и демпфирование масляной пленки, опор и фундаментов, а также масса роторов, опор и фундаментов.

 

Рисунок 2.2. Схема возникновения свободной центробежной силы F при дебалансе ротора.

 

 

Различают колебания трех видов (рисунок 2.3, 2.4).

 

Рисунок 2.3. Виды колебаний у машин.

 

 

Относительные колебания валов. Это быстрые движения вала ротора по отношению к вкладышу подшипника.

Абсолютные колебания опор подшипников. Под этим подразумеваются быстрые движения вкладыша подшипника и корпуса подшипника по отношению к жесткой опорной точке в пространстве.

Абсолютные колебания валов. Это быстрые движения вала ротора по отношению к жестко установленной опорной точке в пространстве.

 

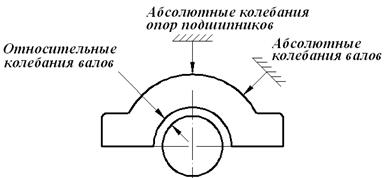
Рисунок 2.4. Виды колебаний и места их измерения (на примере подшипника скольжения).

 

В области механических колебаний приняты три измеряемые величины:

· вибросмещение (амплитуда колебаний) s - отклонение точки измерения от положения покоя; единица измерения - мкм (1 мкм = 10^-6 м);

· виброскорость v - скорость движения точки измерения вокруг своего положения покоя; единица измерения - мм/с;

· виброускорение а - ускорение движения точки измерения вокруг своего положения покоя; единица измерения - м/с².

Когда уровень вибрации оценивается для отдельной электрической машины в испытательном помещении, условия измерения и допустимые значения вибрации определяются по ГОСТ 20815 (МЭК 34-14-82).

Этот же стандарт устанавливает, что при измерении вибрации на месте эксплуатации, следует пользоваться специальными методиками, разработанными для машин конкретных типов.

По ГОСТ 20815 критерием, принятым для оценки интенсивности вибрации машин с частотой вращения 600 об/мин и выше, является среднеквадратичное значение виброскорости, имеющей размерность мм/с и обычно обозначаемой v_e или v_eff; v_e определяют непосредственным измерением или по результатам спектрального анализа в диапазоне от частоты вращения, на которой проводят измерения, до 2000 Гц по формуле

 

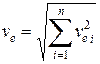
(2.2)

 

где - среднее квадратическое значение виброскорости, полученное при спектральном анализе для i -й полосы фильтра; i = 1, 2... n, при этом первая и n - я полосы фильтра должны включать соответственно нижнюю и верхнюю граничные частоты заданной для измерения полосы частот.

Для крупных машин (с высотой оси более 355 мм) с частотой вращения менее 600 об/мин определяют и нормируют пиковое значение виброперемещения S (мкм).

Интенсивность вибрации машины характеризуется наибольшим значением из числа измеренных в предписанных точках.

Для машин на подшипниках скольжения следует дополнительно учесть соотношения масс и жесткости объекта. Ротор с малой массой сможет побудить жесткую опорную конструкцию с большой массой только к незначительным колебаниям подшипников. Относительные колебания вала при этом в 10-30 раз больше, чем абсолютные колебания подшипников. Тогда в качестве измеряемой величины необходимо выбрать относительное колебание вала. Если масса роторов увеличивается не намного меньше массы подшипниковых узлов со стояками, то относительные колебания валов только в 3-10 раз больше, чем абсолютные колебания подшипников. В этом случае помимо измерения относительных колебаний валов рекомендуется измерять еще абсолютные колебания подшипников, чтобы получить более достоверную информацию о техническом состоянии машины.

Когда масса роторов сопоставима с массой подшипниковых опор или больше, абсолютные колебания валов могут достигнуть примерно таких же самых значений, как абсолютные колебания подшипников. В таких случаях рекомендуется измерять абсолютные колебания валов и корпусов подшипников.

Измерение абсолютных колебаний валов ввиду необходимости специальной измерительной аппаратуры вызывает большие трудности. Поэтому эти колебания учитываются, как правило, при эксплуатации только больших турбоагрегатов электростанций.

Чтобы выяснить причины, вызывающие вибрации насосного агрегата, необходимо провести диагностические работы с частотным анализом вибраций насосного агрегата. При частотном анализе с помощью виброизмерительной аппаратуры определяются все частотные составляющие вибраций, которые вызывают колебание машины.

Для правильной интерпретации частотных составляющих вибрации с присущими неисправностями, возникающими в диагностируемом оборудовании, необходимо четко представлять его конструкцию, знать характерные частотные составляющие вибрации, сопутствующие каждому виду неисправности для диагностируемого оборудования, иметь виброизмерительную аппаратуру, позволяющую определять необходимые частотные составляющие вибрации.

Частотный анализ вибраций с помощью виброизмерительной аппаратуры можно осуществлять, в основном, тремя способами: гармоническим анализом вибраций, полосовым выделением частотных составляющих и при применении перестраиваемых фильтров.

При гармоническом анализе вибрации виброизмерительная аппаратура сама определяет частоту вращения ротора машины, настраивает встроенный фильтр на эту частоту и фильтр «пропускает» только ту часть сигнала возмущения, которая соответствует частоте вращения ротора.

Данная величина вибрации называется 1-й гармонической составляющей вибрации или основной гармоникой вибрации. Еще ее называют оборотной составляющей вибрации. Изменяя положение переключателя прибора, можно увеличить (или уменьшить) в 2, 3, 4... раза частоту, на которую настроится встроенный фильтр и тем самым определить 2, 3, 4... гармонические составляющие вибрации. Если мы настраиваем фильтр на частоту ниже 1-й гармоники, то составляющие вибрации называются субгармониками.

Данный способ выделения гармонических составляющих вибрации является наиболее точным, но требует применения (кроме датчика вибрации) датчика, определяющего частоту вращения вала машины (например, фотоэлектрического или лазерного).

Более простым способом выделения частотных составляющих вибрации является применение полосовых фильтров. Встроенные полосовые фильтры настраиваются на определенную частоту, которая зависит от положения переключателя прибора. При этом фильтр пропускает полосу частот, соответствующую его характеристикам. Поэтому, изменяя положение переключателя, мы можем определить, какие частотные составляющие присутствуют в общем уровне вибрации. Под общим уровнем вибрации понимается вся совокупность вибраций, вызванная имеющимися неисправностями в эксплуатируемом оборудовании.

В ряде виброизмерительных приборов имеется перестраиваемый фильтр. Если это автоматически перестраиваемый фильтр, то прибор сам последовательно изменяет частоту пропускания фильтра, и по изменениям показаний индикатора можно определить, какие частотные составляющие и с какой величиной присутствуют в общем уровне вибрации. Однако визуально это сделать сложно. Поэтому для такого частотного анализа обычно используют самописцы, подключаемые к выходу прибора, и записывают амплитудно-частотную диаграмму, по которой впоследствии определяют отдельные частотные составляющие вибрации.

Для диагностических работ можно использовать любой из этих способов частотного анализа вибрации.

2.2.2. Относительные колебания валов.

 

Ротор, имеющий дебаланс, приводит к колебаниям вала. Центр вала движется во время вращения по траектории, именуемой кинетической траекторией вала (рисунок 2.5).

В случае изотропного вала и изотропных подшипников кинетическая траектория, вызванная дебалансом, составляет круг для каждого сечения ротора. Но обычно подшипники машин анизотропные, т.е. они имеют разную податливость в своих обоих главных направлениях жесткости. Поэтому их кинетическая траектория вала принимает характер эллипса, который в крайнем случае может приобрести форму прямой (см. рисунок 2.6).

 

PS:

Изотропность. - Изотропными телами называются такие, в которых по трем (и по всем другим) взаимно перпендикулярным направлениям упругость одинакова; вместе с тем одинаковы и другие свойства, как-то теплопроводность, электропроводность, скорость распространения света.

 

Величина, форма и положение кинетической траектории вала изменяется в зависимости от частоты вращения. Обычно кинетические траектории с наибольшим отклонением от оси вращения достигают максимума при критической частоте вращения вала.

Кинетическая траектория вала содержит все информации о колебаниях вала ротора. Для получения кинетической траектории вала в одной радиальной плоскости ротора следует закрепить два датчика относительной вибрации в двух перпендикулярных к друг другу направлениях (рисунок 2.7).

Каждый датчик принимает измеряемые в соответствующем направлении вибросмещения вала 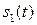и 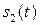. Синфазное сложение мгновенных вибросмещений дает мгновенную кинетическую амплитуду вала в плоскости измерения:

 

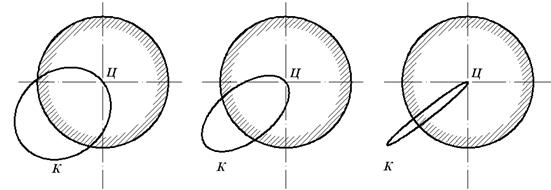
Рисунок 2.5. ‑ Кинетическая траектория вала с изотропными (А) и анизотропными (В и С) подшипниками. Ц – центр вала или центр вращения ротора, К - кинетическая траектория вала

 

Рисунок 2.7. ‑ Схема установки датчиков относительной вибрации для регистрации кинетической траектории вала: 1,2- направления измерений вибрации.

 

(2.3)

 

Пример кинетической траектории вала и соответствующие вибросмещения в двух, находящихся под прямым углом направлениях, приведен на рисунке 2.6. Движение содержит две гармоники - f и 2f; s₁ и s₂ - мгновенные значения амплитуд колебаний s₁(t) и s₂(t) в направлении измерений 1 и 2; s_о1 и s_o2 - наибольшие значения; s_u1 и s_u2 - наименьшие значения; s_max1 и _smax2 - максимальные значения; s_pp1 × s_pp2 - размах колебаний; s_r -мгновенная кинетическая амплитуда вала; s_max - максимальное значение амплитуды вала, максимальная амплитуда; К - кинетическая траектория вала; t - время.

Из возможных величин измерения - вибросмещение, скорость и ускорение - для оценки колебаний вала принимается вибросмещение, измеряемое в микронах (мкм). Величину вибросмещения можно оценить максимальной амплитудой s_max или наибольшим размахом колебаний s_ppm.

Измерение колебаний вала следует всегда проводить в зоне опоры. Максимальная амплитуда колебаний s_max определяется как наибольшее значение кинетической амплитуды s_r(t) в плоскости измерения. Наибольший размах колебаний s_ppm определяется как наибольшее значение зарегистрированных в обоих направлениях измерения размаха колебаний.

 

Рисунок 2.6. ‑ Пример кинетической траектории вала и соответствующие вибросмещения в двух, находящихся под прямым углом, направлениях

 

Для измерения относительных колебаний вала используются бесконтактные датчики вибросмещения, работающие по принципу вихревых токов.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: