 |
Свойства m-последовательностей
|
|
|
|
Свойства m-последовательностей
Период: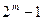 
После такого количества чисел '1' и '-1’ последовательность повторяется, поскольку начальные символы будут теми же. Последовательность должна быть достаточно длинной.
Автокорреляция:
Рассмотрите предыдущую последовательность
| -1 | -1 | -1 | -1 | -1 | -1 | -1 |
Если мы выполним следующую операцию:
= 15, складывающую квадраты чисел ( 
).
то получим,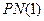 
Так же выполняя операцию: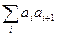 
= -1 =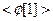 
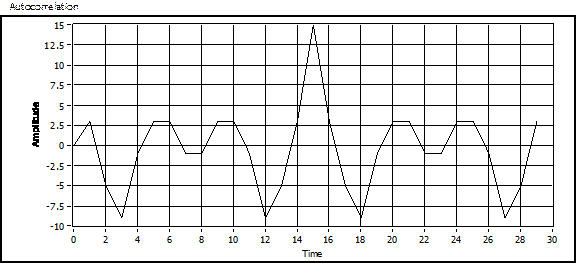
Это – точка автокорреляционной функции для определенного сдвига. Построим функцию на графике, чтобы было по 15 точек до и после 0:
a)
b)
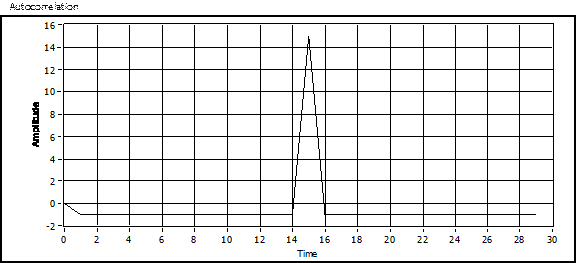
Рисунок 5: Корреляция a) пример последовательности и b) другой пример последовательности с полиномом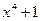 
, созданный с помощью LabVIEW и MathScript
Формульное определение дискретной автокорреляционной функции:
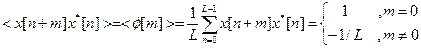
Заметим, если последовательность синхронизована (пик в корреляции = 1), конечный пользователь, имеющий точную последовательность, способен демодулировать сообщение. Другие пользователи получат сигнал с очень маленькой амплитудой относительно начальной. В этом заключается принцип Множественного Доступа с Кодовым Разделением Каналов (Code Division Multiple Access – CDMA), применяемый системами сотовой связи, согласно которому, одни и те же частота и время могут совместно использоваться несколькими пользователями с разными кодами.
Расширение спектра (Spreading)
Блок схема DSSS системы связи, использующей QPSK, представлена на Рисунке 6. Обратите внимание, что к фазовой (I) и квадратурной (Q) компонентам добавляется псевдослучайная последовательность.
Рисунок 6: Блок-схема широкополосного QPSK модулятора
|
|
|
Последовательность должна быть достаточно длинной (что касается сигнала сообщения), чтобы иметь шумоподобный спектр. Скорость передачи широкополосной последовательности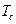 
и скорость передачи сообщения 
связаны соотношением:
В реальных системах N – целое число, которое равно количеству сдвигов фазы PN последовательности для каждого бита сообщения. Например, для систем GPS N = 1024.
Рисунок 7: Расширение спектра сообщения. Каждый бит сообщения будет содержать полную псевдослучайную последовательность
Новое сообщение теперь будет передаваться со скоростью 
и, следовательно, 
.
Выходной сигнал, комбинирующий последовательность с исходным сигналом, равен:
,
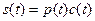где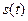 
- отправленный сигнал, 
- псевдошумовой сигнал и c(t) - битовая последовательность.
Демодуляция (Despreading)
Принимаемый сигнал является комбинацией переданного сигнала и шума в канале.
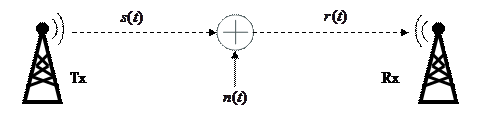
Рисунок 8: Модель канала с добавлением Гауссовского шума. LabVIEW VI 
Полученный сигнал будет снова промодулирован псевдошумовой последовательностью. Обратите внимание, что шум n(t ) также подвергнется этой обработке, однако, благодаря корреляционным свойствам, мощность шума не увеличится.
Полученный сигнал будет комбинацией переданного сигнала и шума:
Мы можем заменить посланный сигнал комбинацией PN последовательности и битовой последовательности.
Модулятор умножит эту последовательность на псевдошумовую :
Если синхронизирована, 
и 
подобны умножению во времени шума на шум, которое дает другой тип шума 
(аналогичный по амплитуде).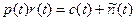 
Рассмотрим идеальный пример, представленный на рисунке 9.
Рисунок 9: Восстановление исходного сигнала двумя разными пользователями. Пользователь 1 имеет правильную последовательность. Пользователь 2 имеет другую последовательность и, следовательно, выходное сообщение будет иметь много ошибок (нет информации)
|
|
|
M-последовательности – основные, но единственные псевдошумовые последовательности. Они нашли применение лишь в системах GPS. С того момента, когда идея расширения спектра сигнала легла в основу CDMA систем, выделились две главные наиболее часто используемые последовательности: Золотые последовательности (WCDMA) и последовательности Уолша- Адамара (Walsh-Hadamard) (IS-95).
|
|
|
