 |
Золотые Последовательности (Gold Sequences)
|
|
|
|
Золотые Последовательности (Gold Sequences)
Золотые последовательности позволяют генерировать больше вариантов с помощью пары m-последовательностей.
Создание золотых последовательностей основано на предпочтительных парах m-последовательностей.
Например, возьмем многочлены 
и 
:
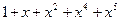Рисунок 10: Пример генератора Золотой последовательности, использовавшей пару m-последовательностей: и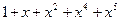
Вспомним, что m-последовательность генерировала только одну последовательность длиной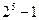 
. Объединяя две последовательности, мы можем получить до 31 ( 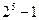) и плюс две m-последовательности, т. е. сгенерировать 33 последовательности, которые могут быть использованы, чтобы передавать другие входные сообщения (других пользователей CDMA).
Пара m-последовательностей и 
золотых последовательностей формируют 
доступных последовательностей, используемых в DSSS. Полезное свойство золотых кодов – их сбалансированность (количество 1 и -1 равно).
Последовательности Уолша-Адамара
Другими последовательностями, часто используемыми в системах CDMA, являются последовательности Уолша-Адамара. Эти последовательности ортогональны (то есть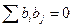 
где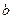 
- строка матрицы), что является удобным в многопользовательских системах. Последовательностями являются строки матрицы Адамара 
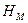, которая для 
определяется в виде:
Для больших матриц используется рекурсия:
Пример для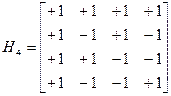 
Ортогональные коды имеют отличительное свойство взаимной корреляции (если не осуществлен никакой сдвиг).
Выводы
Мы изучили различные последовательности, с помощью которых могут передаваться сигналы, ведущие себя подобно шуму. Напоследок мы хотели бы отметить преимущества и недостатки использования широкополосных систем:
|
|
|
Преимущества:
· Секретность. Безопасная связь, поскольку сигнал " замаскирован" под шум
· Не происходит интерференция с другими сигналами в той же полосе.
· Возможность одновременного использования полосы частот несколькими пользователями (CDMA)
· Помехозащищенность
Недостатки:
· Увеличенная ширина полосы частот (радиотехнические схемы для широкополосных систем ведут себя по-разному на различных частотах)
· Увеличение сложности
Литература
[1]. G. L. Stü ber, “Principles of mobile communication, ” Kluwer Academic, Boston 1996.
[2]. J. G. Proakis, “Digital Communications, ” 4th Edition, McGraw-Hill Higher Education.
[3]. T. S. Rappaport, “Wireless communications: principles and practice, ” Pentrice Hall PTR, N. J., 1996.
[4]. T. Pratt, C. W. Bostian and J. E. Allnutt, “Satellite Communications, ” 2nd ed. John Wiley publication, 2002.
[5]. R: Prasad, T. Ojanperä, “An Overview of CDMA Evolution Toward wideband CDMA, ” IEEE communications surveys, Vol. 1, No. 1 Q4 1998.
Кодирование канала
Теорема кодирования канала с шумом
Передача цифровых данных через канал связи с заданной вероятностью ошибки возможна до определенной скорости, зависящей от уровня шума в канале.
Максимальная скорость передачи названа пределом Шеннона или пропускной способностью канала по имени Клода Шеннона, который первым доказал соответствующую теорему. Пропускная способность канала С, выражаемая в бит/с, для фиксированной полосы пропускания BW, в Герцах, мощности сигнала P и мощности шума N, вычисляется по формуле:
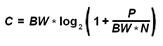
Канальное кодирование – это метод обработки исходных данных, при котором они могут быть восстановлены после прохождения через канал с шумом. Лучшие методы кодирования создают такой поток данных, который приближается к пределу Шеннона с минимальной вероятностью ошибок. Значительное уменьшение вероятности ошибок для потока, меньшего, чем предела Шеннона, достигается за счет сложного кодирования в передатчике и декодирования в приемнике. В качестве альтернативы, относительно простые коды могут достигать снижения вероятности ошибок за счет увеличения полосы пропускания. Скорость передачи кода для всех технологий кодирования канала, обозначается Rc и равна отношению длины данных до кодирования, k, и после кодирования, n, или Rc = k/n. Скорость кода Rc меньше 1, для простых, неэффективных технологий кодирования, и приближается к 1 для более эффективных.
|
|
|
|
|
|
