 |
Технология расширения спектра сигнала прямой последовательностью (Direct Sequence Spread Spectrum)
|
|
|
|
Технология расширения спектра сигнала прямой последовательностью (Direct Sequence Spread Spectrum)
DSSS - методика модуляции для цифровой передачи данных, которая заменяет отдельные биты псевдослучайной битовой последовательностью. Эта битовая последовательность предназначена для расширения спектра. Поскольку скорость передачи пост-модулированного потока выше, эффективно увеличивается и пропускная способность канала. Результирующая скорость передачи равна исходной скорости передачи, умноженной на длину расширяющей последовательности. Каждый бит расширяющего кода называется элементарной кодовой посылкой. Цифровая единица в исходной последовательности будет заменена расширяющим кодом, в то время как 0 будет заменен дополнением расширяющего кода. Чтобы демодулировать сигнал, получатель должен знать расширяющий код.
Основное преимущество DSSS состоит в том, что традиционная узкополосная интерференция не разрушает сигнал, поскольку он теперь «размазан» по большей полосе. Широкополосный шум, однако, будет все еще мешать приему исходного сигнала.
В LabVIEW при использовании Modulation Toolkit расширенные коды могут быть получены с помощью ВП Spread Symbols и декодированы с помощью ВП Despread Symbols.
Литература
[1] John G. Proakis and Masoud Salehi, Communications Systems Engineering.
Фильтрация в Системах Связи
Введение
В цифровых системах связи информация может передаваться с помощью несущего синусоидального колебания посредством изменения его фундаментальных характеристик: фазы, частоты и амплитуды. В физическом канале эти изменения могут быть сглажены в зависимости от фильтров, применяемых при передаче. Фактически, фильтрация играет важную роль для канала связи, поскольку она помогает устранить спектральную утечку, уменьшить ширину канала и ослабить межсимвольную интерференцию (Inter Symbol Interference – ISI).
|
|
|
Основы применения формирующих фильтров
Для выполнения двух важных требований, предъявляемых к беспроводным каналам связи, необходимо использовать формирующие («pulse shaping») фильтры. Эти требования: 1) генерация ограниченных по частоте каналов и 2) уменьшение межсимвольной интерференции (ISI) при многолучевых отражениях сигнала. Фактически, фильтр в виде функции sync, показанный ниже, удовлетворяет этим требованиям, поскольку он эффективно использует частотную область, и благодаря финитности функции, действующей на каждом символьном периоде модулированного сигнала. Импульс sync с FFT-спектром показан ниже.

Рисунок 1: Sync импульс во временной и частотной области
Как видно из рисунка, импульс sync периодичен и имеет максимальную амплитуду в середине символьного интервала. Кроме того, в частотной области импульс будет выглядеть как прямоугольник, который может эффективно ограничить канал связи в определенном частотном диапазоне.
Уменьшение ширины Канала
По существу, модуляция несущей синусоиды приводит к постоянным изменениям (переходам) в её фазе и амплитуде. Ниже показана временная область несущей синусоиды с частотой символов, равной половине частоты несущей. Можно видеть, что без использования фильтрации происходят резкие переходы.
|




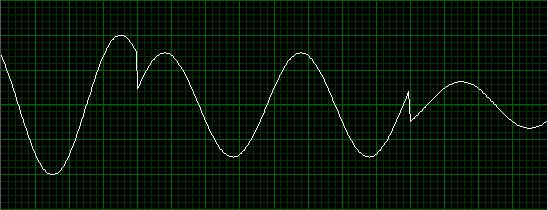
Рисунок 2: Изменения фазы и амплитуды в нефильтрованном модулированном сигнале
Известно, что резкие перепады амплитуды сигнала приводят к возникновению высокочастотных компонентов в частотной области. На рисунке (4) справа показано БПФ нефильтрованного сигнала. Как и следовало ожидать, значительная мощность канала вышла за пределы 1ГГц полосы частот. В многоканальных системах связи концентрация мощности модулированной несущей в ширине полосы пропускания чрезвычайно важно по нескольким причинам. Во-первых, мощность передачи уменьшается, когда сигнал более сконцентрирован в частотном диапазоне. Кроме того, канал, ограниченный в определенной полосе частот, не оказывает влияния на соседние каналы.
|
|
|
Применение формирующего фильтра к модулированной синусоиде сглаживает резкие переходы и ограничивает результирующий сигнал определенной полосой частот. Ниже показана модулированная синусоида во временной области.
|


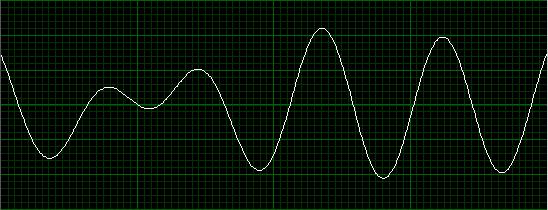
Рисунок3: Сглаженные изменения фазы и амплитуды отфильтрованного модулированного сигнала
Как показывает этот рисунок, при использовании фильтрации переходы фазы и амплитуды происходят более плавно. В результате, частотная информация синусоиды становится более сконцентрированной в определенной полосе частот. Это можно увидеть с помощью БПФ преобразование сигнала.

Рисунок 4: Частотная область фильтрованного и нефильтрованного сигнала
Практические занятия:
Создание математической модели процесса – стр. 95
|
|
|


