Свободные электромагнитные колебания

Глава 17. Электромагнитные колебания

Свободные электромагнитные колебания это происходящие под действием внутренних сил периодическое изменение заряда на конденсаторе, силы тока в катушке, а также электрических и магнитных полей в колебательном контуре.

Ø Незатухающие электромагнитные колебания

Для возбуждения электромагнитных колебаний служит колебательный контур, состоящий из соединённых последовательно катушки индуктивности L и конденсатора ёмкостью С (рис.17.1).

Рассмотрим идеальный контур, т. е. контур, омическое сопротивление которого равно нулю (R=0). Чтобы возбудить колебания в этом контуре, необходимо либо сообщить обкладкам конденсатора некоторый заряд, либо возбудить в катушке индуктивности ток. Пусть в начальный момент времени кон­денсатор заряжен до разности потенциалов U (рис. (рис.17.2, а); следователь­но, он обладает потенциальной энергией 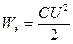. В этот момент времени ток в катушке I = 0. Такое состояние колеба­тельного контура аналогично состоянию математического маятника, отклоненного на угол α (рис. 17.3, а). В это время ток в катушке I=0. После соединения заряженного конденсатора с катушкой, под действием электрического поля, создаваемого зарядами на конденсаторе, свободные электроны в контуре начнут перемещаться от отрицательно заряженной обкладки конденсатора к положительно заряженной. Конденсатор начнёт разряжаться, и в контуре появится нарастающий ток. Переменное магнитное поле этого тока породит вихревое электрическое. Это электрическое поле будет направлено противоположно току и потому не даст ему сразу достигнуть максимального значения. Сила тока будет увеличиваться постепенно. Когда сила в контуре достигнет максимума, заряд на конденсаторе и напряжение между обкладками равно нулю. Это произойдёт через четверть периода t = π/4. При этом энергия электрического поля переходит в энергию магнитного поля W_э=1/2C U²₀. В этот момент на положительно заряженной обкладке конденсатора окажется столько перешедших на неё электронов, что их отрицательный заряд полностью нейтрализует имевшийся там положительный заряд ионов. Ток в контуре начнёт уменьшаться и станет уменьшаться индукция создаваемого им магнитного поля. Изменяющееся магнитное поле снова породит вихревое электрическое, которое на этот раз будет направлено в ту же сторону, что и ток. Поддерживаемый этим полем ток будет идти в прежнем направлении и постепенно перезаряжать конденсатор. Однако по мере накопления заряда на конденсаторе его собственное электрическое поле будет всё сильнее тормозить движение электронов, и сила тока в контуре будет становиться всё меньше и меньше. Когда сила тока уменьшится до нуля, конденсатор окажется полностью перезаряженным.

Состояния системы, изображенные на рис. 17.2 и 17.3, соответствуют последовательным моментам времени Т = 0; ; ; 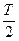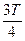и Т.

ЭДС само­индукции, возникающая в контуре, равна напряжению на обкладках кон­денсатора: ε = U

и

Полагая , получаем

(17.1)

Формула (17.1) аналогична дифференциальному уравнению гармонического колебания, рассмотренных в механике; его решением будет

q = q_maxsin(ω₀t+φ₀) (17.2)

где q_max - наибольший (начальный) заряд на обкладках конденсатора, ω₀ -круговая частота собственных колебаний контура, φ₀-начальная фаза.

Согласно принятым обозначениям, откуда

(17.3)

Выражение (17.3) называется формулой Томсона и показывает, что при R=0 период электромагнитных колебаний, возникающих в контуре, определяется только значениями индуктивности L и ёмкости С.

По гармоническому закону изменяется не только заряд на обкладках конденсатора, но и напряжение и сила тока в контуре:

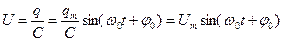(17.4)

 

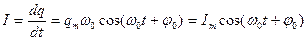(17.5)

 

где U_m и I_m – амплитуды напряжения и силы тока.

Из выражений (17.2), (17.4), (17.5) вытекает, что колебания заряда (напряжения) и тока в контуре сдвинуты по фазе на π/2. Следователь­но, ток достигает максимального значения в те моменты времени, ко­гда заряд (напряжение) на обкладках конденсатора равен нулю, и наоборот.

При зарядке конденсатора между его обкладками появляется электрическое поле, энергия которого

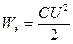или

При разрядке конденсатора на катушку индуктивности в ней возникает магнитное поле, энергия которого

В идеальном контуре максимальная энергия электрического поля равна максимальной энергии магнитного поля:

Энергия заряженного конденсатора периодически изменяется со временем по закону

или

Учитывая, что , получаем

Энергия магнитного поля соленоида изменяется со временем по закону

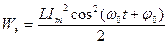(17.6)

Учитывая, что I_m=q_m ω₀, получаем

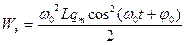(17.7)

Полная энергия электромагнитного поля колебательного контура равна

W =W_э +W_м= (17.8)

В идеальном контуре суммарная энергия сохраняется, электромагнитные колебания незатухающие.

Ø Затухающие электромагнитные колебания

Реальный колебательный контур обладает омическим сопротивлением, поэтому колебания в нём затухают. Применительно к этому контуру закон Ома для полной цепи запишем в виде

 

(17.9)

Преобразовав это равенство:

и сделав замену:

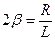и , где β- коэффициент затухания получим

(17.10)
- это дифференциальное уравнение затухающих электромагнитных колебаний.

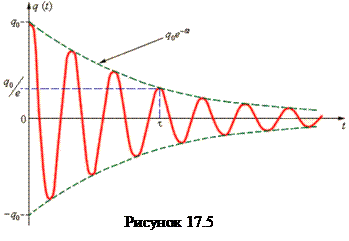
Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 17.5). При малых затуханиях ω ≈ ω₀, решением дифференциального уравнения будет уравнение вида

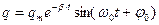(17.11)

Затухающие колебания в электрическом контуре аналогичны затухающим механическим колебаниям груза на пружине при наличии вязкого трения.

Логарифмический декремент затухания равен

(17.12)

Интервал времени в течение, которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.

Добротность Q колебательной системы определяется по формуле:

(17.13)

где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение: добротность – это отношение энергии в колебательной системе к потери энергии за 1 период.

Для RLC-контура добротность Q выражается формулой

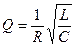(17.14)

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: