 |
Уравнения Колмогорова в теории потоков событий
|
|
|
|
Глава 1. Марковизируемые потоки событий
Рассмотрим некоторые классы потоков событий, обобщающие классы пуассоновских и рекуррентных потоков.
Модулированные пуассоновские потоки
Многочисленные исследования реальных потоков заявок, требований, сообщений, выполненные зарубежными и отечественными специалистами в различных областях, позволили сделать вывод о существенной неадекватности классических моделей потоков (пуассоновских и рекуррентных) реальным данным. Поэтому актуальной является задача существенного расширения множества математических моделей случайных потоков однородных событий, а также развития методов их исследования.
По определению случайным потоком однородных событий называется последовательность 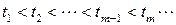 моментов наступления рассматриваемых событий.
моментов наступления рассматриваемых событий.
С другой стороны, обозначив 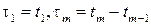 при
при  , случайным потоком однородных событий, будем называть последовательность
, случайным потоком однородных событий, будем называть последовательность 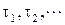 .
.
Случайный поток однородных событий будем также определять в виде случайного процесса  – числа событий рассматриваемого потока, наступивших за время
– числа событий рассматриваемого потока, наступивших за время 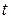 , то есть на интервале
, то есть на интервале 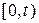 .
.
Рассмотрим класс модулированных пуассоновских потоков.
Пусть задан некоторый случайный процесс  и множество неотрицательных чисел
и множество неотрицательных чисел 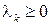 .
.
Случайный поток однородных событий будем называть модулированным пуассоновским (MP-потоком), управляемым случайным процессом  , если выполнены условия
, если выполнены условия
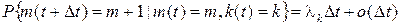 ,
,
 .
.
Среди множества MP-потоков выделим класс марковских модулированных пуассоновских потоков (MMP-потоков).
Модулированный пуассоновский поток будем называть MMP-потоком, если управляющий процесс  является цепью Маркова с непрерывным временем.
является цепью Маркова с непрерывным временем.
Можно рассмотреть и другие классы MP-потоков, управляемых случайными процессами из других классов.
|
|
|
В литературе для MP-потоков также встречается название дважды стохастические потоки.
MAP-потоки
Значительное разнообразие потоков определяется множеством MAP-потоков (Markovian Arrival Process). Их рассмотрение начнём с класса синхронных MAP-потоков.
Пусть задана цепь Маркова  , определяемая матрицей
, определяемая матрицей 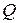 её инфинитезимальных характеристик
её инфинитезимальных характеристик 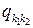 .
.
Случайный поток однородных событий будем называть синхронным MAP-потоком, если моменты наступления его событий совпадают с моментами изменения состояний управляющей этим потоком цепи Маркова  .
.
Выделим некоторое состояние цепи Маркова  , которое будем называть репродуктивным.
, которое будем называть репродуктивным.
Случайный поток однородных событий будем называть рекуррентным PH-потоком (рекуррентным потоком фазового типа), если его события наступают тогда и только тогда, когда управляющая цепь попадает в репродуктивное состояние.
Очевидно, что в таком потоке длины интервалов стохастически независимы и одинаково распределены, поэтому рассматриваемый поток является рекуррентным. А так как длины интервалов имеют фазовое или PH-распределе-ние, то использованное для него название оправдано.
Теперь выделим некоторое подмножество 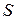 состояний управляющей цепи. Элементы
состояний управляющей цепи. Элементы  будем называть репродуктивными состояниями. Дадим следующее определение.
будем называть репродуктивными состояниями. Дадим следующее определение.
Случайный поток однородных событий будем называть полумарковским PH-потоком (полумарковским потоком фазового типа), если его события наступают тогда и только тогда, когда управляющая цепь попадает в любое репродуктивное состояние.
Определённые выше потоки, принадлежат достаточно широкому классу общих MAP-потоков.
Для определения общего MAP-потока, рассмотрим MMP-поток, и будем полагать, что для любых 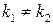 заданы вероятности
заданы вероятности 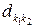 того, что в момент перехода цепи Маркова из состояния
того, что в момент перехода цепи Маркова из состояния  в состояние
в состояние 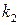 наступает ещё одно событие, а с вероятностью
наступает ещё одно событие, а с вероятностью 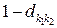 событие в этот момент не наступает. Определённый таким образом случайный поток однородных событий будем называть общим MAP-потоком или просто MAP-потоком.
событие в этот момент не наступает. Определённый таким образом случайный поток однородных событий будем называть общим MAP-потоком или просто MAP-потоком.
|
|
|
Для того, чтобы вернуться к MMP-потоку достаточно в MAP-потоке положить все 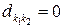 .
.
Если в MAP-потоке положить все 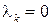 , а вероятности
, а вероятности 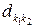 задать в виде
задать в виде
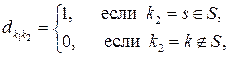
то получим полумарковский PH-поток.
Если в предыдущем случае множество 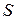 включает одно единственное состояние, то получаем рекуррентный PH-поток.
включает одно единственное состояние, то получаем рекуррентный PH-поток.
Все вышеперечисленные потоки являются ординарными. Определим достаточно общую модель неординарного потока.
BMAP-потоки
Потоки данного класса предложены Д.Лукантони в 1991 году. Они получили название групповых марковских входящих потоков (Batch Markovian Arri
val Process – BMAP).
Заявки в BMAP-потоке поступают группами случайного числа. Моменты реализации групп образуют MAP-поток. Будем полагать, что количество заявок в различных группах стохастически независимы и определены распределениями  , если управляющая потоком цепь Маркова находится в состоянии
, если управляющая потоком цепь Маркова находится в состоянии 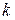 , а также распределениями
, а также распределениями 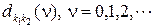 в момент перехода цепи из состояния
в момент перехода цепи из состояния  в состояние
в состояние 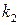 .
.
Таким образом, для задания BMAP-потока необходимо задать инфинитезимальную матрицу 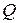 , набор неотрицательных чисел
, набор неотрицательных чисел 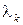 , а также набор распределений вероятностей
, а также набор распределений вероятностей 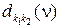 числа
числа 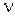 заявок в группах, поступающих в потоке.
заявок в группах, поступающих в потоке.
Очевидно, что идентификация реальных потоков моделями BMAP-потоков представляет определённые проблемы в связи с необходимостью оценки значений большого числа параметров таких потоков, поэтому ниже будут использованы, главным образом модели MAP-потоков.
Полумарковские потоки
Рассмотрим двумерный однородный марковский случайный процесс 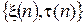 с дискретным временем
с дискретным временем 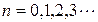 , первая компонента
, первая компонента  , которого принимает значения из некоторого дискретного множества. Для определённости будем полагать, что
, которого принимает значения из некоторого дискретного множества. Для определённости будем полагать, что
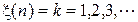 .
.
Вторая компонента 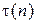 рассматриваемого процесса принимает неотрицательные значения (вообще говоря, из непрерывного множества).
рассматриваемого процесса принимает неотрицательные значения (вообще говоря, из непрерывного множества).
По определению, марковской переходной функцией  двумерного однородного марковского случайного процесса
двумерного однородного марковского случайного процесса 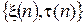 называется
называется

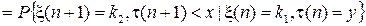 . (1.1)
. (1.1)
Будем рассматривать только такие двумерные случайные процессы 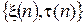 , для марковских переходных функций которых выполняются равенства
, для марковских переходных функций которых выполняются равенства
|
|
|
 =
= 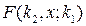 , (1.2)
, (1.2)
то есть условное распределение (1.1) не зависит от второго условия (не зависит от значений второй компоненты). В этом случае марковскую переходную функцию 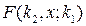 будем обозначать
будем обозначать
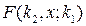 =
=  .
.
Матрицу 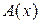 , элементами которой являются функции
, элементами которой являются функции  , будем называть полумарковской.
, будем называть полумарковской.
Случайный поток однородных событий
 (1.3)
(1.3)
будем называть полумарковским или SM-потоком, заданным матрицей 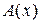 , если для длин
, если для длин 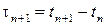 его интервалов выполняются равенства
его интервалов выполняются равенства
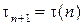 .
.
В силу свойства (1.2), первая компонента 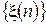 рассматриваемого двумерного марковского процесса
рассматриваемого двумерного марковского процесса 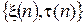 также является марковским процессом, точнее цепью Маркова с дискретным временем и матрицей
также является марковским процессом, точнее цепью Маркова с дискретным временем и матрицей  вероятностей
вероятностей 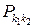 переходов за один шаг, определяемой равенством
переходов за один шаг, определяемой равенством
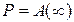 .
.
Эта цепь Маркова для рассматриваемого SM-потока называется вложенной по моментам времени (3).
Вторая компонента  , вообще говоря, является немарковским процессом (последовательностью зависимых случайных величин), но для её элементов можно определить условные функции распределения
, вообще говоря, является немарковским процессом (последовательностью зависимых случайных величин), но для её элементов можно определить условные функции распределения
 ,
,
а также по формуле полной вероятности в стационарном режиме и безусловную функцию распределения
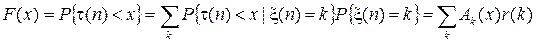 ,
,
где 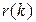 – стационарное распределение вероятностей значений цепи Маркова
– стационарное распределение вероятностей значений цепи Маркова 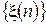 , которое определяется системой уравнений
, которое определяется системой уравнений
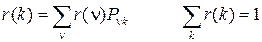 .
.
Эту систему уравнений можно переписать в матричном виде, обозначив векторы
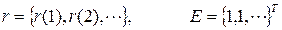 ,
,
следующим образом
 .
.
Если компоненты  двумерного процесса
двумерного процесса 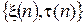 , условно независимы, то есть для элементов
, условно независимы, то есть для элементов  полумарковской матрицы
полумарковской матрицы 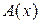 выполняется равенство
выполняется равенство
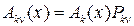 ,
,
то полумарковский поток будем называть потоком марковского восстановления.
Уравнения Колмогорова в теории потоков событий
|
|
|


