 |
Метод асимптотического анализа MMP-потоков в условии предельно редких изменений состояний потока
|
|
|
|
Как было указано выше, MMP-поток определяется набором неотрицательных величин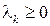 
и цепью Маркова 
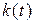, заданной матрицей 
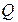её инфинитезимальных характеристик.
Значения цепи Маркова 
, определяющие условные интенсивности 
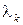наступления событий в потоке, будем называть состояниями MMP-потока.
Значения инфинитезимальных характеристик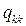 
определяют продолжительности времени пребывания потока в 
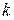-ом состоянии.
В системе уравнений для MMP-потока обозначим 
получим систему
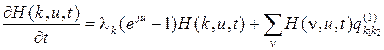. (1.67)
Выше было рассмотрено асимптотическое условие растущего времени 
В этом разделе рассмотрим асимптотическое условие предельно редких изменений состояний MMP-потока, формализуя которое, положим 
при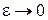 
. При выполнении этого условия продолжительность времени пребывания потока в 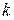-ом состоянии неограниченно возрастает, что оправдывает название рассматриваемого асимптотического условия.
Систему (1.67) перепишем в виде
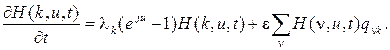(1.68)
Будем полагать, что для решения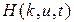 
этой системы выполняются начальные условия
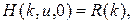
где значения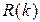 
определены выше.
Решение 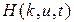системы (1.68), зависящее от малого параметра 
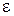, обозначим
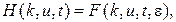(1.69)
тогда для 
получаем следующую задачу Коши
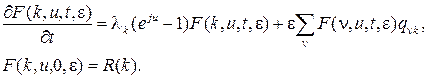(1.70)
Эту задачу будем решать в асимптотическом условии 
Асимптотика первого порядка
Можно доказать следующее утверждение.
Теорема 3. Если существует предел
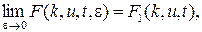
то
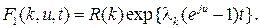(1.71)
Доказательство.
В задаче (1.70) выполним предельный переход при 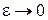, получим равенства
которые представляют собой совокупность по всем 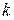независимых задач Коши, каждая из которых имеет следующее решение
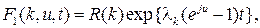
совпадающее с (1.70).
Теорема доказана.
Следствие. В условии предельно редких изменений состояний MMP-потока распределение вероятностей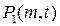 
числа 
событий потока, наступивших за время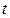 
, является взвешенной с весами 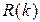суммой пуассоновских распределений с параметрами 
, то есть имеет вид
|
|
|
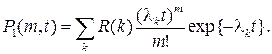(1.72)
Доказательство.
Так как для характеристической функции величины можно записать равенство
то при 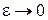в силу (1.69) и (1.71) имеет место приближённое (асимптотическое) равенство
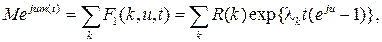
из которого следует равенство (1.72).
Следствие доказано.
Равенство (1.71) будем называть асимптотикой первого порядка в условиях предельно редких изменений состояний MMP-потока.
Равенство (1.72) будем называть аппроксимацией первого порядка допредельного распределения в асимптотическом условии предельно редких изменений состояний MMP-потока.
Асимптотика произвольного порядка
Для более детального исследования допредельной модели, решение задачи Коши (1.70) запишем в виде
и докажем следующее утверждение.
Теорема 4. Если для функции существует разложение
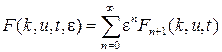, (1.73)
то коэффициенты этого разложения имеют вид
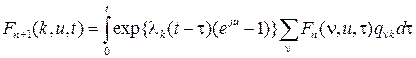. (1.74)
Доказательство.
Подставив разложение (1.73) в (1.70), получим равенства
.
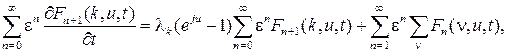
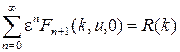Приравнивая коэффициенты при одинаковых степенях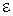 
, при 
для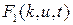 
, получим задачу Коши
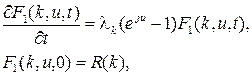
рассмотренную выше, решение 
которой имеет вид (1.71).
При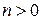 
, для 
получим следующую задачу Коши
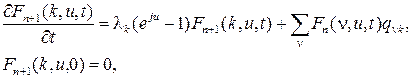
в которой, аналогично вышеизложенному, система представляет собой совокупность независимых по всем 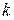задач Коши для неоднородных линейных дифференциальных уравнений с нулевыми начальными условиями, решение которых имеет вид совпадающий с (1.74).
Теорема доказана.
Доказанная теорема формирует рекуррентный алгоритм (1.74) последовательного нахождения асимптотик всё более высокого порядка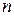 
.
Для нахождения соответствующих аппроксимаций распределения вероятностей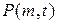 
целесообразно воспользоваться процедурой, изложенной в десятом разделе этой главы, реализация которой сводится к численному либо аналитическому интегрированию (1.64).
|
|
|
|
|
|
