 |
Потоки с дискретной компонентой
|
|
|
|
Основной задачей исследования случайных потоков однородных событий является проблема нахождения распределения вероятностей
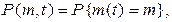
которую для рассматриваемых потоков можно решить, определив распределение вероятностей двумерного случайного процесса 
, то есть
откуда найти одномерное маргинальное распределение
.
Так как процесс является двумерной цепью Маркова, то для распределения вероятностей 
нетрудно составить систему уравнений Колмогорова, решив которую, найдём распределение .
Приведём примеры таких систем уравнений для различных классов потоков.
1. Для MMP-потока запишем равенства
,
откуда получим
(1.4)
2. Для синхронного MAP-потока аналогично запишем
откуда получим
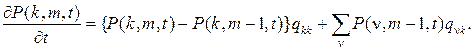(1.5)
3. Для рекуррентного PH-потока с репродуктивным состоянием 
можно записать
следовательно, система уравнений Колмогорова в этом случае имеет вид
(1.6)
4. Для полумарковского PH-потока с множеством S репродуктивных состояний запишем следующие равенства
откуда получим
(1.7)
5. Для общего MAP-потока запишем следующие равенства
откуда, положив 
, получим
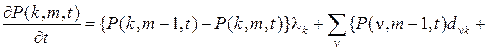
(1.8)
Выбирая в этом уравнении соответствующие значения параметров 
и 
, получим все ранее составленные уравнение Колмогорова для вышеперечисленных потоков.
Совершенно аналогично нетрудно получить уравнение Колмогорова для BMAP-потока.
Потоки с непрерывной компонентой
Рассмотрим потоки с непрерывной компонентой.
6. Для исследования рекуррентного потока определим процесс 
как длину интервала от момента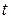 
до момента 
наступления следующего события в рассматриваемом потоке.
Для рекуррентного потока двумерный случайный процесс 
является марковским, поэтому для его распределения вероятностей
|
|
|
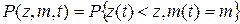
по формуле полной вероятности нетрудно получить равенство
,
из которого следует, что распределение 
является решением уравнения Колмогорова
. (1.9)
Равенство, определяющее уравнение (1.9) получено следующим образом.
Для его левой части запишем
.
Относительно случайного события 
, рассматриваемого в момент времени 
сформулируем две гипотезы, реализуемые в момент времени :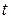
,
,
для которых
,
здесь при выполнении второй гипотезы остаточная длина 
интервала отличается от полной длины на бесконечно-малую порядка 
, так как событие потока наступило в интервале 
. Эти две гипотезы образуют не полную группу событий, но в формуле полной вероятности слагаемые, соответствующие другим гипотезам дают бесконечно-малую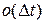 
.
Поток марковского восстановления
Для потока марковского восстановления двумерный процесс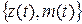 
является немарковским, поэтому определим ещё один случайный процесс так, что бы составленный трёхмерный процесс стал марковским.
Определим случайный процесс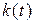 
равенством
,
то есть процесс 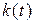на интервале 
сохраняет то значение, которое он получил в начале этого интервала и которое совпадает со значением 
вложенной цепи Маркова. Отметим, что реализации процесса 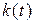непрерывны справа.
Для потока марковского восстановления трёхмерный процесс 
является марковским, поэтому для его распределения вероятностей
по формуле полной вероятности нетрудно получить равенство
из которого следует, что распределение вероятностей 
является решением уравнения Колмогорова
. (1.10)
Полумарковский поток
Для полумарковского потока, заданного полумарковской матрицей 
, предложенный выше трёхмерный случайный процесс , будет немарковским, поэтому вместо процесса 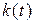определим процесс 
следующим образом
,
то есть процесс на интервале 
принимает и сохраняет то значение 
, которое вложенная цепь Маркова примет в конце рассматриваемого интервала. Отметим, что реализации процесса непрерывны слева. Для полумарковского потока трёхмерный случайный процесс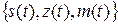 
будет марковским, поэтому для его распределение вероятностей
|
|
|
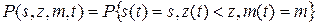
по формуле полной вероятности нетрудно получить равенство
,
из которого следует, что распределение вероятностей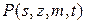 
является решением уравнения Колмогорова
. (1.11)
|
|
|
