 |
Глава 6 Механические колебания
|
|
|
|
§6.1 Свободные колебания
Движения, которые точно или приблизительно повторяются через одинаковые промежутки времени, называются механическими колебаниями.
Механическая система, находящаяся в состоянии колебательного движения, называется осциллятором. Примерами простейших механических осцилляторов являются пружинный, математический и физический маятник. Колебания этих систем совершается под действием возникающей силы, пропорциональной смещению системы из положения равновесия. Если возвращающая сила при малых колебаниях зависит от смещения линейно, то осциллятор называется гармоническим.
Если же возвращающая сила зависит от смещения более сложно, например Fв = -кх+gx2+hx3, то такой осциллятор называется ангармоническим.
В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания.
Свободными (собственными) колебаниями называют такие, которые происходят под действием внутренних сил без внешних воздействий за счёт первоначально полученной телом энергии. Такие колебания возникают в системе после того, как система была выведена из состояния равновесия и предоставлена самой себе. Примером таких колебаний является пружинный, математический и физический маятник. Отличительной особенностью систем, в которых происходят свободные колебания, является наличие у них положения устойчивого равновесия. Именно около этих положений и совершаются свободные колебания.
§6.1.1 Пружинный маятник
Рассмотрим свободные колебания пружинного маятника. Наша цель — определить траекторию движения тела.
Пружинный маятник – это некоторое тело на пружине, массой которой можно пренебречь по сравнению с массой тела. Пружина может располагаться либо вертикально (вертикальный пружинный маятник), либо горизонтально (горизонтальный пружинный маятник (рис.4.1).
|
|
|
Пусть тело массой m укреплено на пружине, упругость которой k. В отсутствии сил трения на тело, выведенное из положения равновесия, действует сила упругости Fупр = -kx, пропорциональная смещению тела х от положения равновесия и направленная к этому положению. Благодаря инертности колеблющееся тело не
останавливается в положении равновесия (когда сила упругости обращается в нуль), а продолжает двигаться в прежнем направлении.
|
ma= F или 
,
где 
следует
(6.1)
Разделим части уравнения (6.1) на массу колеблющегося тела m и получаем
(6.2)
Сделаем замену
(6.3)
Величина ω0 является собственной частотой колебаний маятника.
Учитывая это, формулу (6.2) можно записать в виде
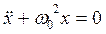(6.4)
Выражение (6.4) является дифференциальным уравнением свободных незатухающих колебаний.
Из формулы (4.3) учитывая, что 
получим, что
периода колебаний пружинного маятника равен
(6.5)
§6.1.2 Математический маятник
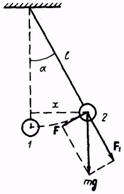Математический маятник – это идеализированная система, представляющая собой материальную точку, подвешенную на длинной, тонкой, невесомой и нерастяжимой нити, находящейся в поле тяжести Земли (рис. 6.2).
При отклонении материальной точки от положения равновесия на малый угол α, такой, что выполняется условие sinα = α, на тело будет действовать возвращающая сила F=-mgsinα=-mgα, пропорциональная смещению. Знак минус указывает, что сила направлена в сторону, противоположную смещению. Силы, которые по своей природе не являются силами упругости, но формально подчиняются закону Гука, называются квазиупругими силами.
По второму закону Ньютона
m a =-mgα, (6.6)
где 
, (6.7)
|
|
|
Сделаем замену
(6.8)
и получим
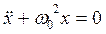(6.9)
- дифференциальное уравнение математического маятника
и период колебаний математического маятника
(6.10)
§4.1.3 Физический маятник
Физический маятник, представленный на рис.6.3 является твердым телом, имеющим неподвижную ось вращения, не проходящую через его центр масс (точка С). При отклонении тела от положения равновесия на малый угол α на тело действует момент силы тяжести относительно горизонтальной оси вращения, проходящей через точку О,
М = -mgℓsinα (6.11)
[ℓ — расстояние от центра масс (точка С) до оси вращения О; знак минус указывает, что направление момента сил тяжести противоположно направлению отклонения].
Так как при малых углах sinα = α, то М = -mgℓα
Исходя из основного уравнения динамики вращательного движения, найдем
Jβ = M, где 
(6.12)
Тогда
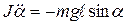или 
Разделим последнее уравнение на J, получим
(6.13)
Введём замену 
откуда получим
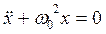(6.14)
- дифференциальное уравнение физического маятника
и период колебаний физического маятника
(6.15)
Величину
(6.16)
называют приведённой длиной физического маятника (длина такого математического маятника, который имеет такой же период колебаний, что и данный физический маятник).
§6.1.4 Гармонические колебания
Общим решением полученных дифференциальных уравнений является выражение вида:
x = Asin(ω0t+φ0) или x = Acos(ω0t+φ0) (6.17)
Оно определяет смещение осциллятора от положения равновесия х в зависимости от времени t.
Колебания, при которых координаты колеблющегося тела меняются с течением времени по закону синуса (или косинуса), называются гармоническими.
Уравнение (6.17) называется уравнением колебаний гармонического осциллятора.
Рассмотрим входящие в выражение (6.17) величины, которыми характеризуются любые колебательные движения:
v А – амплитуда колебаний (максимальное отклонение гармонического осциллятора от положения равновесия);
v ωt+φ0 - фаза колебаний (скалярная величина, определяющая состояние колебательной системы в данный момент времени;
v φ0 - начальная фаза (величина, определяющая состояние колебательной системы в начальный момент времени);
v ω - циклическая, или угловая частота собственных колебаний гармонического осциллятора (число колебаний за 2π секунд).
|
|
|
Важнейшее свойство гармонических колебаний – их изохронность, т.е. независимость периода от амплитуды и начальной фазы. Именно это свойство позволяет использовать маятники в часах для отсчёта равных промежутков времени.
|
|
|
