 |
Сложение взаимно перпендикулярных гармонических колебаний
|
|
|
|
Рассмотрим осциллятор, изображённый на рисунке. Он представляет собой материальную точку, закреплённую на пружине в центре рамы, такой осциллятор способен совершать два независимых взаимно перпендикулярных гармонических колебания по оси Х и по оси У.
Пусть материальная точка одновременно участвует в двух колебаниях: одно направлено вдоль оси ОХ, другое — вдоль оси ОУ. Допустим, что частоты колебаний одинаковы, т.е. ω01 = ω02= ω0 тогда траекторию движения материальной точки в параметрической форме задают следующие уравнения:
х =A1sinω0t (6.49 а)
у =A2sin(ω0t + φ0) (6.49 б)
(φ0 - разность фаз обоих колебаний).
Возбудив одновременно оба колебания. Поскольку смещение х и у являются функцией времени, то и результирующее смещение будет зависеть от времени: тело будет перемещаться в плоскости ХОУ по некоторой траектории, вид которой зависит от соотношения частот и начальных фаз обоих колебаний.
Таким образом, задача о сложении двух взаимно перпендикулярных колебаний сводится к задаче отыскания траектории движения осциллятора. Чтобы определить траекторию результирующего колебания, нужно из заданных уравнений исключить время. Из уравнения (6.49 а) найдём
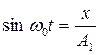тогда 
(6.50)
Как известно, sin(α+β) = sinαcosβ + cosαsinβ, тогда уравнение (6.49 б) можно записать в виде
откуда
Возводя это выражение в квадрат, имеем
После приведения подобных членов получим
(6.51)
Уравнение (6.51) представляет собой уравнение эллипса, отнесенного к осям ОХ и ОУ.
Рассмотрим частные случаи, вытекающие из этого уравнения.
· При φ = 0 уравнение (6.51) принимает вид
(6.52)
откуда 
, т. е. получим уравнение прямой, проходящей через начало координат.
· При φ =±π уравнение (6.51) принимает вид
|
|
|
откуда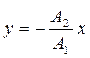 
(6.53)
Результирующее движение и в этом случае представляет собой гармоническое колебание вдоль прямой.
· При φ = π/2 уравнение (6.51) переходит в уравнение
(6.54)
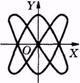
Это уравнение эллипса (рис. 6.17). При равенстве амплитуд, т. е. А1= А2, эллипс превращается в окружность.
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Вид фигур Лиссажу зависит от отношения частот 
и разности начальных фаз φ01 - φ02 слагаемых колебаний.
Примеры решения задач
Пример. Складываются два гармонических колебания, описываемых уравнениями 
, м и 
,м. Сложив эти колебания с помощью метода векторных диаграмм, запишите уравнение результирующего колебания. Определите амплитуду и начальную фазу результирующего колебания.
Дано: , м; ,м.
Найти: х(t); А; φ.
Решение. Согласно заданным в задаче уравнениям, складываемые гармонические колебания имеют одинаковые циклические частоты (ω1=ω2=ω = π с-1); первое колебание характеризуется амплитудой А1=0,2м, второе – амплитудой А2=0,3м. Начальная фаза первого колебания 
, второго - 
.
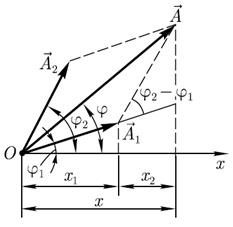Сложим колебания, воспользовавшись методом векторных диаграмм (см. рисунок). Поскольку векторы 
и 
вращаются с одинаковой угловой скоростью ω (равна циклической частоте колебаний), разность фаз (φ1-φ2) между ними сохраняется постоянной.
Δφ=φ2-φ1= 
.
Результирующее колебание (см.рисунок)
x=х1+х2=Acos(ωt+φ), (1)
где
, (2)
(3)
Вычисляя, получаем А=48,4 см; tgφ=1,11; φ=arctgφ =48º.
Используя полученные данные для А и, уравнение результирующего колебания можно записать в виде:
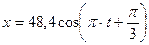, см (4)
т.е. сумма двух гармонических колебаний одного направления с одинаковой частотой является гармоническим колебанием (4) с той же частотой и амплитудой и фазой, определяемыми выражениями (2) и (3).
|
|
|
Ответ: 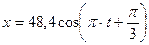,см; А=48,4см; 
.
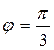Пример. Результирующее колебание, получающееся при сложении двух гармонических колебаний одного направления с одинаковыми амплитудами и начальными фазами, равными нулю, мало отличающихся по частоте, описывается уравнением x= Acos2t∙cos48t (t – в секундах).Определите циклические частоты складываемых колебаний и период биений результирующего колебания.
Дано: В1=В2=В; φ 1= φ 2= 0;. x= Acos2t∙cos48t.
Найти: ω1; ω 2; Т б.
Решение. При сложении двух гармонических колебаний одного направления с одинаковыми амплитудами, начальными фазами, равными нулю, и близкими частотами
х1= Вcosω1t;
х2= Вcosω2t,
результирующее колебание х имеет периодически изменяющуюся амплитуду:
. (1)
Учитывая, что результирующее колебание, заданное в задаче, имеет вид
x= Acos2t∙cos48t (2)
из уравнений (1) и (2) найдём
; 
Решая два последних уравнения, получим ω1=50с-1; ω2=46с-1.
Период биений
Ответ: ω1=50с-1; ω 2=46с-1; Т б=1,57с.
Пример. Точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями x= 0,2sinπt, м и у= -0,1cosπt,м. Определите: 1) уравнение траектории точки, вычертите траекторию движения точки, указав направление её движения; 2) скорость точки в момент времени t =0,2с.
Дано: x= 0,2sinπt, м; и у= -0,1cosπt,м; t=0,2с.
Найти: 1) y(x); 2) υ.
Решение. Для нахождения уравнения траектории точки следует из заданных в задаче уравнений исключить время t. Преобразуем уравнения
x= 0,2sinπt (1)
у= -0,1cosπt (2)
к виду
; 
Возведя оба уравнения в квадрат и сложив их, получаем
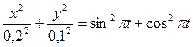
или
- искомое уравнение траектории точки – уравнение эллипса с полуосями А=0,2м и В=0,1 м (см. рисунок).
Чтобы определить направление движения точки, рассмотрим, как изменяется её положение с течением времени. При t=0 координаты точки х(0), у(0) = -0,1м. Далее, например, при t= 0,5с координаты точки х(0,5) =0,2 м,
у(0,5) =0. Следовательно, точка движется по траектории против часовой стрелки (см. рисунок).
Скорость точки при её движении по эллипсу
где 
и 
- скорость точки в слагаемых колебаниях. Поскольку складываются взаимно перпендикулярные колебания, то
, (3)
Из формул (1) и (2) получим
(4)
|
|
|
(5)
Подставив выражения (4) и (5) в формулу (3), найдём искомую скорость в момент времени t:
Ответ: 1) ; 2) υ=0,54м/с.
|
|
|
