Методы представления колебаний

Существуют различные методы описания гармонических колебаний. Приведём некоторые из них.

1. Аналитический метод

Задаётся уравнение колебаний гармонического осциллятора

х=Аsin(ωt+φ₀)

по которому и определяется смещение его от положения равновесия в любой момент времени.

2. Графический метод

Строятся график гармонического колебания (рис.6.4) х=Аsin(ωt+φ₀). По оси абсцисс (ОХ) откладывается время t или фаза колебаний ωt+φ₀, по оси ординат (ОУ) – смещение х от положения равновесия.

 

3. Метод векторной диаграммы

Этот метод состоит в следующем. Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде А колебания, а направление образует с осью х угол, равный начальной фазе колебания (рис. 6.5). Если привести этот вектор во вращение с угловой скоростью ω₀, то проекция конца вектора на ось х будет перемещаться в пределах от +А до -А, а колеблющаяся величина будет изменяться со временем по закону

x = Asin(ω₀t+φ₀), совершая гармоническое колебание.

 

§ 6.1.6 Скорость и ускорение колеблющейся точки

Чтобы найти скорость материальной точки при гармоническом колебании, возьмем производную от смещения колеблющейся точки x = Asin(ω₀t+φ₀) по времени:

(6.18)

где υ_max = Аω₀ — максимальная скорость (амплитуда скорости).

На основании тригонометрических формул преобразуем (4.18):

(6.19)

Сравнивая выражения для смещения и скорости замечаем, что фаза скорости на больше фазы смещения, т.е. скорость опережает по фазе смещение на Продифференцировав (4.18), найдем ускорение:

(6.20)

где а _max = А ω₀² - максимальное ускорение (амплитуда ускорения).

Вместо (6.20) запишем

а = а _max соs [π + (ω₀t+φ₀)] (6.21)

Из сравнения (6.21) и (6.17) следует, что фазы ускорения и смещения различаются на π, т. е. эти величины изменяются в противофазе. Это значит, что при положительном максимальном смещении ускорение максимально, но отрицательно. На рисунке показаны графические зависимости смещения, скорости и ускорения от времени (рис.6.6, а) и их векторные диаграммы (рис.6.6, б).

§ 6.1.7 Кинетическая и потенциальная энергии колебательного движения

Гармонический осциллятор обладает как кинетической, так и потенциальной энергией, которые последовательно переходят друг в друга при колебаниях осциллятора. Полная энергия осциллятора равна сумме кинетической и потенциальной энергии:

Е = Е_к+Е_п (6.22)

Кинетическая энергия осциллятора, колеблющегося по гармоническому закону, вычисляют по формуле:

(6.23)

с учётом mω² = k

Потенциальную энергию колебательного движения найдём, исходя из формулы для потенциальной энергии упругой деформации:

(6.24)

Складывая кинетическую и потенциальную энергию, получим полную механическую энергию материальной точки, колеблющейся по гармоническому закону:

(6.25)

Полученное выражение показывает, что энергия гармонического осциллятора от времени не зависит, т.е. с течением времени остаётся величиной постоянной, а зависит только от квадрата амплитуды и частоты.

При отсутствии сил трения полная механическая энергия системы не изменяется:

(6.26)

Графически зависимости кинетической, потенциальной и полной механической энергий колеблющейся системы от времени показаны на рис. 4.7, а.

 

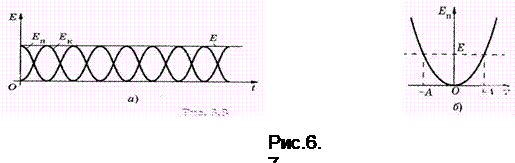Потенциальная яма (ограниченная область пространства, в которой потенциальная энергия меньше, чем в не её), соответствующая гармоническому колебанию, изображена на рис. 6.7, б. Она определяется зависимостью 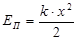. Отложив на оси ординат полную механическую энергию Е, по графику определяют интервал координат (-А, +А), за пределы которого частица, обладающая такой энергией, выйти не может.

 

Примеры решения задач

Пример. Тело массой m=2 кг подвешено к упругой пружине, совершает гармонические колебания. Определите жёсткость k пружины, если за время t=1,5мин число N полных колебаний равно 60.

Дано: m=2кг; t=1,5мин=90с; N=60.

Найти: k.

Решение: Период гармонических колебаний тела, подвешенного на пружине (пружинный маятник),

,

где m- масса тела; k- жёсткость пружины.

С другой стороны, период колебаний

,

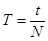где t – время, за которое совершается N полных колебаний.

Приравняв оба выражения

Найдём искомую жёсткость пружины

Ответ: k=35,1 Н/м.

 

Пример. При подвешивании грузов массами m₁ и m₂=2 m₁ к свободным пружинам пружины удлинились одинаково (Δх=15см). Пренебрегая массой пружин, определите: 1) периоды колебаний грузов; 2) какой из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз?

Дано: m₁; m₂=2 m₁; Δх=15см = 0,15м; А₁=А₂=А.

Найти: 1) Т₁; Т₂; 2) .

Решение. Из условия равновесия грузов на пружине следует, что

m₁g=k₁Δx и m₂g=k₂Δx

(удлинение в обоих случаях одинаково), где k₁ и k₂ – соответственно жёсткость первой и второй пружин. Тогда

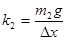и (1)

Периоды колебаний грузов на пружинах соответственно

и (2)

Подставив выражения (1) в формулу (2), найдём

и

т.е. периоды колебаний равны:

.

Механическая энергия груза, колеблющегося на пружине,

(3)

где А – амплитуда колебаний; - циклическая частота.

Поскольку по условию задачи А₁=А₂=А и нашли, что Т₁=Т₂, поэтому искомое отношение энергий, согласно формуле (3),

.

Следовательно, Е₁ в два раза меньше, чем Е₂.

Ответ: Т₁=Т₂=0,776 с; Е₂=2Е₁.

Пример. Один из математических маятников совершил N₁=20 колебаний, другой за то же время совершил N₂=12 колебаний. Определите длины обоих маятников, если разность их длин Δℓ=16см.

Дано: t₁=t₂=t; N₁=20; N₂=12; Δℓ=16см = 0,16м.

Найти: ℓ₁; ℓ₂.

Решение. Период колебаний

,

где t – время, за которое совершилось полных колебаний.

По условию задачи,

N₁Т₁=N₂ Т₂ (1)

где периоды колебаний первого и второго математических маятников

и (2)

(где g – ускорение свободного падения).

Из выражения (1) и (2) следует, что

(3)

Учитывая, что

Δℓ=ℓ₂-ℓ₁ (4)

И решая уравнения (3) и (4), найдём искомые длины математических маятников:

; .

Ответ: ℓ₁=9см; ℓ₂=25 см.

 

Пример. Тонкий обруч подвешен на вбитый в стену гвоздь и совершает гармонические колебания с периодом Т=1,56 с в плоскости, параллельной стене. Определите радиус обруча.

Дано: Т=1,56с.

Найти: R.

Решение. Тонкий обруч под действием силы тяжести совершает колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс. С обруча (см.рисунок).

Это – пример физического маятника.

Период колебаний физического маятника

(1)

где I– момент инерции маятника относительно оси, проходящей через точку подвеса О; ℓ - расстояние между точкой подвеса О и центром масс С маятника; m- масса обруча; g - ускорение свободного падения.

Согласно теореме Штейнера, момент инерции I диска относительно оси не проходящей через его центр масс,

I=I₀+m a ²,

где I₀–момент инерции обруча относительно оси, проходящей через центр масс обруча; a - расстояние между осями. Учитывая, что I₀=mR² (тонкостенный диск); а =R, последняя формула запишется в виде

I= mR²+ mR²= 2mR². (2)

Подставив выражение (2) в формулу (1), учитывая, что ℓ=R, найдём искомый радиус диска:

Ответ: R=30,2см.

 

Пример. Физический маятник в виде тонкого однородного стержня длиной 0,5м совершает гармонические колебания вокруг неподвижной оси, проходящей через точку подвеса О, не совпадающую с центром масс С. Определите, на каком расстоянии х от центра масс должна находиться точка подвеса, чтобы циклическая частота колебаний была максимальна.

Дано: ℓ =0,5 м; ω=ω_max.

Найти: x.

Решение: Период колебаний физического маятника

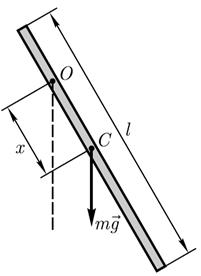где I – момент инерции стержня относительно горизонтальной оси, проходящей через точку подвеса О, не совпадающую с центром масс С стержня (см. рисунок); m - масса стержня; g- ускорение свободного падения; х – расстояние между точкой подвеса О и центром масс С.

Циклическая частота

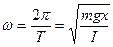(1)

Согласно теореме Штейнера, момент инерции стержня относительно оси, проходящей через точку подвеса, находящуюся от центра масс на расстоянии х,

(2)

где -момент инерции стержня относительно горизонтальной оси, проходящей через центр масс стержня (через середину стержня).

Подставив (2) в (1), получим

(3)

Найдём экстремум функции (3) (по условию задачи циклическая частота максимальна):

; ,

откуда

ℓ²-12х²=0

(нас интересуют только положительные решения), т.е. искомое расстояние

Ответ: х=14,4см.

 

Пример. Материальная точка массой m=10г совершает гармонические колебания с амплитудой А=40см и периодом Т=4с. В начальный момент времени t₀=0 смещение x₀ достигает максимально возможного значения. Запишите уравнение колебаний точки.

Дано: m=10г=10^-2кг; А= 40см; Т=4с.

Найти: x(t).

Решение: Уравнение гармонических колебаний

х=Аcos(ω₀t+φ₀), (1)

 

где циклическая частота (учли условие задачи); φ₀ - начальная фаза колебаний.

Согласно условию задачи, в момент времени t₀=0 смещение x₀=А (А- амплитуда колебаний). Тогда уравнение (1) можно записать в виде

откуда cos φ₀ =1. Следовательно, начальная фаза φ₀=0.

Используя найденные значения ω₀, φ₀ и заданное А, искомое уравнение колебаний точки:

,м

Пример 6.1. Материальная точка, совершающая гармонические колебания с

частотой ν=1Гц, в момент времени t=0 проходит положение, определяемое координатой x₀=4см, со скоростью υ₀=-16см/с. Определите амплитуду колебаний.

Дано: ν=1Гц; t=0; x₀=4см (4∙10^-2м); υ₀=-16см/с (-16∙10^-2м/с).

Найти: А

Решение: Уравнение гармонических колебаний материальной точки

x=Аcos(ω₀t+φ₀) (1)

где ω₀=2πν.

Скорость точки, совершающей гармонические колебания,

(2)

В начальный момент времени (t=0) смещение и скорость материальной точки, согласно (1) и (2)

х₀=Аcosφ₀ (3)

υ₀=-ω₀Аsinφ₀ (4)

Поделив (4) на (3), получим

откуда

Из формулы (3) амплитуда колебаний равна

Учитывая, что cosφ₀=0, 843, получаем А=4,74 см.

Ответ: А=4,74 см.

 

Пример. Материальная точка массой m=10г совершает гармонические колебания с частотой ν=0,2 Гц. Амплитуда колебаний равна 5 см. Определите: 1) максимальную силу, действующую на точку; 2) полную энергию колеблющейся точки.

Дано: m=10г=10^-2кг; ν=0,2 Гц; А=5см=5∙10^-2м

Найти: 1) Fmax; 2) E

Решение: Уравнение гармонических колебаний материальной точки

x=Аcos(ω₀t+φ₀) (1)

Тогда скорость и ускорение колеблющейся точки

Согласно второму закону Ньютона, сила, действующая на точку,

F=m a =-Aω₀²m∙cos (ω₀t+φ₀).

F=F_max при cos(ω₀t+φ₀)= ±1, поэтому искомое максимальное значение силы

F_max=Aω₀²m=4π²ν²Am

Учли, что ω₀=2πν.

Полная энергия колеблющейся точки

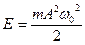
Подставив сюда ω₀, найдём искомую полную энергию:

Е=2π²mν²A²

Ответ: 1) F_max=0,8мН; 2) Е=19,7мкДж.

 

Пример. Материальная точка массой m= 5г совершает гармонические колебания с амплитудой А=10см и частотой ν =1Гц. В начальный момент времени t₀=0 смещение x₀=А. Определите кинетическую и потенциальную энергии в момент времени t = 2,2с

Дано: m=5г=5∙10^-3кг; А=10см=10∙10^-2м; ν=1Гц; t₀=0; x₀=А; t = 2,2с.

Найти: Т; П.

Решение: Кинетическая и потенциальная энергии материальной точки, совершающей гармонические колебания,

; (1)

; (2)

где циклическая частота ω₀=2π ν =2π с^-1 (учли условие задачи); φ₀- начальная фаза.

Уравнение гармонических колебаний:

x=Аcos(ω₀t+φ₀)

которое для условий задачи запишется в виде

x=0,1cos(2πt+φ₀),м

Для определения начальной фазы учтём, что при t₀=0 смещение x₀=А. Тогда можем, согласно (3), записать

x₀=0,1cos(2π∙0+φ₀)=0,1 м,

т.е. cosφ₀=1 и φ₀=0. Таким образом, фаза колебаний равна 2πt c^-1.

При заданной фазе колебаний уравнения (1) и (2) примут вид:

;

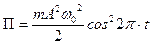
Ответ: Т=892мкДж; П=94,2мкДж.

 

§ 6.2 Затухающие колебания

До сих пор мы рассматривали свободные колебания осциллятора без учёта сопротивления среды, в которой происходят эти колебания.

В реальных условиях на колеблющееся тело всегда действуют силы сопротивления (трения), в результате чего амплитуда с течением времени уменьшается и колебания становятся затухающими.

Пусть маятник колеблется в вязкой среде (рис.). В этом случае на осциллятор кроме возвращающей силы F_упр = -kx будет действовать ещё одна сила – сила сопротивления среды F_с. При малых колебаниях скорость движения осциллятора мала, поэтому сила сопротивления пропорциональна скорости и направлена в противоположную сторону:

(6.27)

где r – коэффициент сопротивления среды, зависящий от плотности среды и геометрических размеров осциллятора; - относительная скорость движения осциллятора и среды.

Согласно второму закону Ньютона, результирующая этих сил и определяет то ускорение, с которым колеблется осциллятор. Уравнение движения осциллятора в этом случае имеет вид:

или

Разделив последнее уравнение на m, получим:

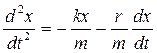
Введя обозначения 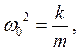и , имеем

или

(6.28)

- дифференциальное уравнение затухающих колебаний

где δ – коэффициент затухания; ω₀ – круговая частота собственных колебаний.

Решение этого уравнения записывается в виде:

x = A₀е^-δt sin(ωt+φ₀) (6.29)

Выражение А=±А₀ е^-δt, есть переменная во времени амплитуда колебания; А₀— амплитуда в момент t = 0; ω -частота затухающих колебаний; φ₀-начальная фаза колебаний.

График этой функции изображён на рисунке (кривая 1)пунктирнаялиния 2изображает ход убывания амплитуды. Осциллятор колеблется по закону синуса, но амплитуда колебания с течением времени уменьшается по экспоненте. Затухания происходят тем быстрее, чем больше δ, т.е. с увеличением внутреннего трения среды и уменьшением массы осциллятора.

Наглядной характеристикой затухания является отношение двух амплитуд, отличающихся по времени на период Т. Это соотношение называется декрементом затухания

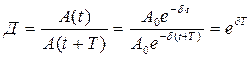(6.30)

Прологарифмируем это выражение:

(6.31)

Значение θ=δТ называется логарифмическим декрементом затухания.

Время в течении которого амплитуда убывает в е раз, называется временем жизни осциллятора. За время жизни τ осциллятора успевает совершить N колебаний.

(6.32)

Следовательно, логарифмический декремент затухания есть величина, обратная числу колебаний осциллятора за время его жизни.

Так как , то отсюда вытекает один из возможных методов экспериментального определения коэффициента сопротивления среды. Измерив отношение амплитуд за период и определив период находят δ, а потом по формуле рассчитывают r.

Частота ω свободных затухающих колебаний будет меньше частоты свободных колебаний осциллятора ω₀:

ω ² = ω₀² - δ² (6.33)

Это происходит потому, что сопротивление уменьшает скорость движения осциллятора. Однако уменьшение скорости частично компенсируется уменьшением амплитуды колебания, поэтому изменение частоты незначительно.

Период затухающих колебаний зависит от коэффициента сопротивления rи определяется формулой:

(6.34)

Уменьшение амплитуды колебания со временем приводит к непрерывному убыванию полной энергии осциллятора.

Так как Е∼А², А=А₀е^-δt то Е=Е₀е^-2δt

где Е₀ – значение энергии в начальный момент времени t = 0. Наличие сопротивления среды (силы трения), приводит к рассеянию (диссипации) механической энергии осциллятора, т.е. к необратимому переходу её в тепловую энергию.

§ 6.3 Вынужденные колебания. Резонанс

Для того, чтобы колебания осциллятора были незатухающими, надо компенсировать потери энергии на преодоления сопротивления среды. Это можно сделать следующим способом. Пусть пружинный маятник с железным грузом находится в поле тяжести электромагнита, по обмотке которого проходит переменный ток (рис):

I = I₀ sin ωt (6.35)

Магнитная сила, действующая на маятник, меняется по тому же закону F_в = F₀ sin ωt. Эта периодически изменяющаяся внешняя сила, действующая на осциллятор, называется вынуждающей силой.

Колебания, возникающие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями.

Получим дифференциальное уравнение вынужденных колебаний.

Ускорение, приобретаемое осциллятором, определяется тремя силами, действующими на него: вынуждающей силой, силой сопротивления и возвращающей (квазиупругой) силой:

F_в = F₀ sin ωt (6.36)

F_с = - r υ

F_упр = -kx

Дифференциальное уравнение вынужденных колебаний в общем случае имеет вид

(6.37)

разделим на m, сохраняю обозначения предыдущего параграфа и полагая ещё , приводим уравнение к виду

(6.38)

Это и есть дифференциальное уравнение вынужденных колебаний.

Решение этого уравнения состоит из двух слагаемых:

x = A₀е^-δt sin(ωt+φ₀)+А sin(ωt+φ₀) (6.39)

Первое слагаемое – свободные затухающие колебания осциллятора, которые по истечению некоторого времени, называемого временем установления, исчезает, второе слагаемое – вынужденные колебания; А – амплитуда колебаний; ω - частота вынужденных колебаний, совпадающая с частотой вынуждающей силы; φ₀- сдвиг по фазе между фазой вынужденных

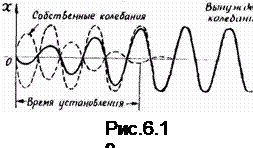колебаний и фазой вынуждающей силы.

На рисунке показано установление вынужденных колебаний.

Вынужденные колебания являются гармоническими с частотой равной частоте вынуждающей силы.

Амплитуда А зависит от амплитуды и частоты вынуждающей силы.

(6.40)

Фаза вынужденных колебаний определяется из условия

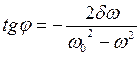(6.41)

Знак «-»указывает на то, что вынужденные колебания отстают по фазе от вынуждающей силы.

Зависимость амплитуды колебаний от частоты вынуждающей силы при различных δ приведены на рис. При ω → 0 амплитуда стремится к предельной величине, равной смещению осциллятора под действием постоянной силы F₀:

(6.42)

Когда частота вынуждающей силы приближается к частоте собственных колебаний осциллятора, амплитуда колебаний возрастает и при некоторой частоте достигает максимального значения. Это явление называется резонансом. Значение резонансной частоты может быть найдено из условия минимума подкоренного выражения.

Найдём производную подкоренного выражения по ω и приравняем её к нулю:

у = ω₀² - 2 ω₀²ω² + ω⁴ + 4δ²ω²

(у - подкоренное выражение),

Сократив на 4ω, имеем -ω₀² + ω² + 2δ² =0, откуда

(6.43)

Максимальное значение амплитуды при резонансе равно.

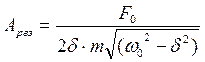(6.44)

Амплитуда будет тем больше, чем меньше δ. При δ → 0, когда частота вынуждающей силы совпадает с собственной частотой колебаний осциллятора ω_р = ω₀, амплитуда вынужденных колебаний стремится к бесконечности:

А_max→ ∞.

Существуют и такие колебательные системы, которые сами регулируют периодическое восполнение растраченной энергии и поэтому могут колебаться длительное время. Незатухающие колебания, существующие в какой-либо системе при отсутствии переменного внешнего воздействия, называются автоколебаниями, а сами системы — автоколебательными. Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы, в отличие от вынужденных колебаний они не определяются внешними воздействиями.

Классическим примером механической автоколебательной системы являются часы, в которых маятник (или баланс) является колебательной системой, пружина (или поднятая гиря) — источником энергии, а анкер — регулятором поступления энергии от источника в колебательную систему. Некоторые биологические системы (сердце, легкие) являются автоколебательными.

 

Примеры решения задач

 

Пример. Запишите уравнение затухающих колебаний материальной точки, если смещение х₀ точки при составляет 10см, период затухающих колебаний Т=3с, логарифмический декремент затухания θ=0,03, начальная фаза колебаний равна нулю.

Дано: ; и х₀=10см=0,1м; Т= 3с; θ=0,03.

Найти: 1) х(t).

Решение. Уравнение затухающих колебаний, если начальная фаза равна нулю, имеет вид:

, (1)

Где А₀ - амплитуда колебаний в момент времени t=0.

Циклическая частота

(2)

Коэффициент затухания δ найдём из выражения для логарифмического декремента затухания: θ=δТ, откуда

.

Амплитуду А₀ найдём из начальных условий (х₀=10см при =1с), согласно уравнению (1), где

,

откуда

.

Подставив в формулы (2), (3) и (4) заданные цифры найдём 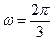с^-1; δ=0,01; А₀=10,1см. Тогда, подставив эти значения в уравнение (1), запишем искомое уравнение затухающих колебаний:

Ответ:

Пример. Маятник совершил 100 полных колебаний, при этом его амплитуда уменьшилась в 10 раз. Определить логарифмический декремент затухания маятника.

Дано: N=100; .

Найти: θ.

Решение. Логарифмический декремент затухания

, (1)

где условный период затухающих колебаний (ν - частота колебаний); δ – коэффициент затухания.

Амплитуда затухающих колебаний в момент времени t=0.

Из формулы (1) найдём δ= ν θ, где частоту ν вычислим, зная число N полных колебаний за время t, за которое произошло указанное уменьшение амплитуды:

,

откуда 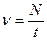и тогда

. (3)

Подставив выражение (3) в формулу (2), получаем

,

Откуда искомый декремент затухания

Ответ: θ=0,023

 

Пример. Логарифмический декремент θ затухания камертона, колеблющегося с частотой ν=100Гц, составляет 0,002. Определите промежуток времени, за который амплитуда возбужденного камертона уменьшится в 50 раз.

Дано: ν=100Гц; θ=0,002; .

Найти: t.

Решение. Амплитуда затухающих колебаний изменяется со временем по закону

, (1)

где А₀ – начальная амплитуда (в момент времени t=0); δ - коэффициент затухания.

Логарифмический декремент затухания θ =δТ, где 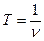- условный период затухающих колебаний. Тогда

δ=θ ν

и выражение (1) можно записать виде

,

откуда искомый промежуток времени

Ответ: t =19,6 с

 

Пример. Точка массой m=20 г совершает затухающие колебания, начальная амплитуда А₀ которых равна 6см, начальная фаза φ₀=0, коэффициент затухания δ=1,6 с^-1. В результате действия на это тело внешней периодической силы установились вынужденные колебания, описываемые уравнением x=3cos(10πt-0,75π), см. Найдите: 1) уравнение собственных затухающих колебаний; 2) уравнение внешней периодической силы.

Дано: m=20г=0,02кг; x=3cos(10πt-0,75π), см; x=0,03cos(10πt-0,75π), м; φ₀=0; А₀ = 6см=0,06м; δ=1,6 с^-1.

Найти: 1) х(t); 2) F(t).

Решение. Уравнение собственных затухающих колебаний с нулевой начальной фазой

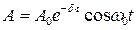(1)

Для определения собственной частоты ω₀ колебательной системы запишем выражение для сдвига фаз φ между собственными и вынужденными колебаниями

(2)

где ω – циклическая частота внешней вынуждающей силы, которая, согласно заданному в задаче уравнению вынужденных колебаний, равна 10π. Из этого же уравнения следует, что φ = -0,75π, т.е. tgφ=1. Тогда, согласно (2),

,

откуда после подстановки числовых значений получаем ω₀=10,5π с^-1.

Уравнение (1) собственных затухающих колебаний после подстановки числовых значений запишется в виде:

, м.

Уравнение внешней вынуждающей силы

F=F₀cosωt,

где F₀ и ω - соответственно амплитуда и частота внешней вынуждающей силы (по условию задачи ω =10π c^-1).

Зная выражение для амплитуды вынужденных колебаний

(из заданного уравнения вынужденных колебаний А=0,03 м), найдём амплитуду вынуждающей силы:

.

Подставив числовые значения, получаем F₀=8,85∙10^-2 Н. Тогда искомое уравнение внешней периодической силы

F=8,85∙10^-2 cos10πt, Н.

Ответ: , м., F=8,85∙10^-2 cos10πt, Н.

Пример. Колебательная система совершает затухающие колебания с частотой ν =800Гц. Определите резонансную частоту ν_рез, если собственная частота ν₀ колебательной системы составляет 802 Гц..

Дано: ν =800Гц; ν₀ =802 Гц.

Найти: ν_рез.

Решение. Циклическая частота затухающих колебаний

, (1)

где ω₀-собственная циклическая частота колебательной системы; δ – коэффициент затухания.

Резонансная частота

(2)

Из уравнений (1) и (2) находим

ω₀²=ω²+δ²; (3)

ω₀²=ω²_рез+2δ². (4)

Умножив уравнение (3) на 2 и вычитая из него (4), получаем

ω²_рез=2ω²- ω₀² (5)

Учитывая, что ω=2πν, из уравнения (5) найдём искомую резонансную частоту:

Ответ: ν_рез=798Гц

 

§ 6.4 Сложение гармонических колебаний, направленных по одной прямой

Рассмотрим механическую систему из трёх маятников, изображённую на рисунке (рис.6.12). Два нижних маятника 1 и 2, которые могут колебаться в вертикальных плоскостях, вызывают колебания маятника 3. При одновременном действии маятников 1 и 2 маятник 3 суммирует колебания, обусловленные нижними маятниками. Происходит сложение колебаний одного направления, и маятник 3 совершает колебание х = х₁ + х₂. Найдём это результирующее колебание. Пусть колебания маятника 3, возникающее при действии нижних маятников, происходят с одинаковой частотой, с той же частотой колеблется маятник 3: ω₀₁ = ω₀₂= ω₀

Запишем уравнения для смещения маятника 3:

x₁=A₁sin(ω₀₁t + φ₀₁) (при неподвижном 2)

x₂=A₂sin(ω₀₂t + φ₀₂) (при неподвижном 1)

Для нахождения результирующего колебания воспользуемся методом векторных диаграмм.

Изобразим положение векторов А₁ и А₂ в начальный момент времени (рис. 6.13), углы между этими векторами и осью ОХ равны начальным фазам складываемых колебаний φ₀₁ и φ₀₂. Вектор А характеризует результирующее колебание.

Рис. 6.12

Так как А₁ и А₂ вращаются с одинаковой угловой

скоростью, то и сумма их – вектор А- будет вращаться с той же угловой скоростью, т. е. результирующее движение является гармоническим с круговой частотой ω₀:

х=x₁+ x₂=A₁sin(ω₀t + φ₀₁) +A₂sin(ω₀t + φ₀₂) =Asin(ω₀t+φ₀) (6.45)

Значение амплитуды результирующего колебания найдём на основании теоремы косинусов

А² = А₁²+ А₂² - 2А₁А₂ соs (φ₀₂ - φ₀₁) и

(6.46)

Амплитуда сложного колебания зависит от разности начальных фаз исходного колебания.

Проанализируем полученное выражение.

· Если разность начальных фаз равна чётному числу π, т.е. φ₀₂ - φ₀₁= 0, 2π, 4π, … 2kπ, где k = 0, 1, 2,..., тогда соs 2kπ = 1. В этом случае колебания совпадают по фазе и амплитуда результирующего колебания принимает максимальное значение, равное сумме амплитуд слагаемых колебаний

(6.47)

 

При равенстве амплитуд А₁ = А₂ размах колебаний маятника 3 возрастает вдвое.

· Если разность начальных фаз равна нечётному числу π, т.е. φ₀₂ - φ₀₁= π, 3 π, 5 π, … (2k + 1)π, где k = 0, 1, 2, тогда соs (2k + 1) π = -1. В этом случае колебания совершаются в противоположных фазах и результирующая амплитуда минимальна и равна разности ам

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: