Следствия из уравнения Бернулли

В качестве следствий из уравнения Бернулли рассмотрим два случая: горизонтальное течение жидкости и истечение жидкости из отверстия.

1. При горизонтальном течении жидкости (например, в горизонтальной трубе) (h₁= h₂), поэтому уравнение (1.91) принимает вид

(8.7)

т. е. при горизонтальном течении жидкости сумма динамического и статического давлений не изменяется при отсутствии трения.

Динамическое давление связано с движением жидкости и проявляется в том случае, если жидкость при встрече с препятствием теряет скорость (υ→ 0). На неподвижную площадку, перпендикулярную скорости течения, жидкость оказывает давление , а на площадку, ориентированную вдоль линии тока — давление Р. Как следует из формулы (8.7), давление Р меньше там, где скорость потока больше (сужение трубки тока).

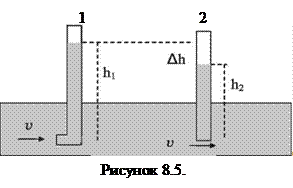Статическое давление измеряется с помощью манометра 2, нижний срез которого параллелен направлению потока (рис. 8.5). Если измерительная трубка 1 имеет изгиб и отверстие трубки направлено навстречу потоку, то частицы жидкости, входя в отверстие, тормозятся, т. е. возникнет сила торможения, и трубка покажет большее давление. Манометр 1 называется трубкой Пито, он измеряет полное давление — сумму статического и динамического давлений.

Разность уровней в трубках 1 и 2 определяет динамическое давление. На этом основано измерение скорости потока или скорости тел, движущихся в жидкостях или газе, например измерение скорости макетов самолетов в аэродинамических трубах.

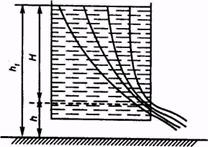2. При истечении жидкости из отверстия будем считать, что внешнее давление Р (например, атмосферное) неизменно и выходное отверстие по сечению мало по сравнению с площадью поверхности жидкости в сосуде (рис. 8.6).

Скорость υ частиц жидкости в сечении выходного отверстия считаем одинаковой. Одинаковой будет и скорость движения частиц поверхности, так как ее поверхность остается горизонтальной. Напишем урав­нение Бернулли для любой трубки тока, одно сечение которой лежит на выходном отверстии, другое — на поверхности жидкости в сосуде:

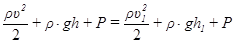
или

Так как h₁-h₂ = Н (см. рис. 1.25) и скорость υ» υ₁, то членом υ₁² можно пренебречь. Тогда

υ²=2gН,

откуда (8.8)

Следовательно, скорость истечения будет такой же, как и в том случае, если бы частицы жидкости свободно падали с высоты h.

Формула (8.8) получила название формулы Торричелли, она справедлива как для боковых, так и для донных отверстий и не зависит от угла наклона выходного отверстия.

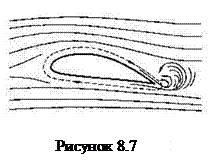3. Возникновение подъемной силы крыла самолета тоже является следствием уравнения Бернулли. При обтекании крыла самолета набегающим потоком воздуха на задней кромке крыла образуется завихрение, в котором воздух вращается против часовой стрелки (если крыло движется справа налево). По закону сохранения момента импульса должен возникнуть круговой поток по часовой стрелке. Такое движение воздуха возникает вокруг крыла. В результате скорость воздушного потока над крылом оказывается больше, чем под крылом. Но согласно уравнению Бернулли, там где скорость больше, давление меньше. Значит давление воздуха на нижнюю часть крыла самолета больше, чем на верхнюю. Эта разность давлений и создает подъемную силу.

Заметим еще, что на уравнении Бернулли основано действие многих технических устройств и, в частности, работа пульверизатора и карбюратора.

Уравнение Бернулли широко применяется в технике, например для расчетов водопроводов, нефтепроводов, газопроводов, насосов и т. п. На его основании сконструирован ряд приборов и устройств, таких как расходомер Вентури, карбюратор, водоструйный насос (эжектор), трубка Пито и т. д.