Движение тел в вязкой среде. Закон Стокса.

Вязкость проявляется не только при движении жидкости или газ; по сосудам, но и при движении тел в жидкости или газе. При небольшие скоростях тел, в соответствии с уравнением Ньютона, сила сопротивления движущемуся телу пропорциональна вязкости жидкости, скорости движения тела и зависит от размеров тела. Так как невозможно указать общую формулу для силы сопротивления, то ограничимся рассмотрением частного случая.

Наиболее простой формой тела является шар. Для него зависимость силы сопротивления от перечисленных выше факторов выражается законом Стокса:

F_c = 6π η r υ (8.23)

где r — радиус шара; υ — скорость его движения. Этот закон получен в предположении, что стенки сосуда не влияют на движение тела. Закон Стокса справедлив лишь при малых числах Рейнольдса (см. § 8.6).

При падении шара в вязкой среде (рис. 8.12) на него действуют три силы: а) сила тяжести Р= 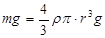; выталкивающая (архимедова) сила 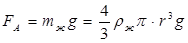, где m — масса вытесненной шаром жидкости, ρ_ж — ее плотность; в) F_тр— сила

сопротивления, вычисляемая по формуле (8.21).

Пусть шар, свободно падая в воздухе, попадает в жидкость. Жидкость тормозит движение шара и его скорость уменьшается. Так как сила сопротивления прямо пропорциональна cкорости, то и она будет уменьшаться до тех пор, пока движение не станет равномерным. В этом случае (рис. 8.12)

(8.24)

 

в скалярной форме

mg +F_А + F_с = 0

 

при подстановке соответствующих выражений для сил

(8.25)

υ₀ — скорость равномерного движения (падения) шара. Из (8.25) получаем

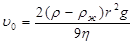(8.26)

Отсюда запишем формулу, которую используют для нахождения вязкости:

(8.27)

 

§ 8.6 Ламинарное и турбулентное течения. Число Рейнольдса

Наблюдения показывают, что в жидкости возможны две формы движения: ламинарное движение и турбулентное.

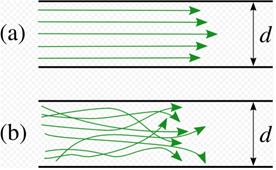
Рассмотренное ранее течение жидкости является слоистым, или ламинарным.

Ламинарное течение — течение жидкости, при котором слои скользят друг относительно друга, не перемешиваясь (рис. а). Для него справедливы уравнения Бернулли и Пуазейля. Увеличение скорости течения вязкой жидкости (газа) вследствие неоднородности давления по поперечному сечению трубы создает завихрение, и движение становится вихревым или турбулентным.

Турбулентное течение — течение, сопровождающееся образованием вихрей и перемешиванием слоёв.

При турбулентном течении жидкости или газа скорость частиц в каждом месте непрерывно и хаотически изменяется, движение является нестационарным.

С увеличением скорости потока ламинарное течение может перейти в турбулентное, а скорость, при которой происходит этот переход, называется критической.

Характер течения жидкости в трубе зависит от свойств жидкости, скорости её течения, размеров трубы и определяется так называемым числом Рейнольдса:

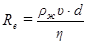(8.28)

ρ_ж — плотность жидкости (газа); υ— средняя по сечению трубыскорость жидкости (газа); d - диаметр трубы.

При малых значениях числа Рейнольдса наблюдается ламинарное течение; при (Rе > Rе_кр), (Rе_кр критическое значение) ламинарное течение переходит в турбулентное. Например, для гладких цилиндрических труб Rе_кр ≈ 2300.

 

Примеры решения задач

Пример. Полый шар плавает на границе двух несмешивающихся жидкостей (см. рисунок) так, что соотношение частей шара во второй и первой жидкости равно . Плотности жидкостей и тела соответственно равны ρ₁=0,8г/см³, ρ₂ =1г/см³ и ρ =2,7 г/см³. Определите объём шара V, если размер его внутренней полости V₀=20см³.

Дано: ; V₀=20см³=2∙10^-5м³; ρ₁=0,8г/см³=8∙10²кг/м³; ρ₂=1 г/см³=1∙10³кг/м³; ρ=2,7 г/см³=2,7∙10³кг/м³.

Найти: V.

Решение. Поскольку шар находится в равновесии, сила тяжести Р, действующая на тело, уравновешивается силой Архимеда F_А:

Р= F_А.

Учитывая, что

Р= ρ(V-V₀)g

и

F_А = m₁g+ m₂g

(ρ – плотность материала шара; V- его объём; V₀- объём внутренней полости шара; g - ускорение свободного падения; m₁ и m₂ – соответственно масса жидкостей в объёмах V₁ и V₂), можно записать

ρ ₁gV₁+ ρ ₂gV₂= ρ (V₁+ V₂ – V₀)g (1)

Из выражения (1), учитывая, что V₂= n V₁ (условие задачи) найдём

Искомый объём шара

Ответ: V=30,1см³.

 

Пример. В сообщающиеся трубки с водой площадью сечения S=0,5см² долили в левую масло объёмом V₂=40мл, в правую керосин объёмом V₂=30мл. Определите разность Δh установившихся уровней воды в трубках, если плотность воды

ρ =1г/см³, плотность масла ρ₁ =0,9 г/см³, плотность керосина ρ₂ =0,8 г/см³.

Дано: S=0,5 см²=0,5∙10^-4м²; V₁=40мл=4∙10^-5м³; V₂=30мл=3∙10^-5м³; ρ=1г/см³= 1∙10³кг/м³; ρ₁=0,9 г/см³= 0,9∙10³кг/м³; ρ₂=0,8 г/см³= 0,8∙10³кг/м³.

Найти: Δh.

Решение. Предположим, что уровень воды в левом сосуде понизится (см. рисунок). Для уровня поверхности воды в левом сосуде давление равно давлению столба масла

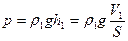, (1)

где h₁- высота столба масла; V₁- объём масла; S- площадь сечения трубки. Для правого сосуда давление на той же горизонтали будет равно сумме давлений столба керосина и избыточного столба воды высотой Δh

, (2)

где h₂- высота столба керосина.

Поскольку давление на одной горизонтали одинаково, приравняв выражения (1) и (2), найдём

,

Откуда искомая разность уровней

Ответ: Δh=24см.

Пример 8.1. Открытый цилиндрический сосуд, стоящи на ножках высотой h₁=1,33м, заполнен водой до отметки h=3,8м (см. рисунок). Пренебрегая вязкостью воды, определите площадь сечения S цилиндра, если через отверстие диаметром d₁=2.5 см у его основания струя, вытекающая из отверстия, падает на пол на расстоянии ℓ=4.5м от цилиндра.

Дано: h₁=1,33м; d₁=2.5 см=2,5∙10^-2м; ℓ=4.5м; h=3,8 м.

Найти: S.

Решение. Согласно уравнению неразрывности,

Sυ = S₁υ₁

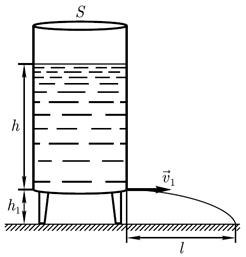где υ – скорость понижения воды в баке; υ₁- скорость вытекания струи; S₁- площадь отверстия. Тогда

.

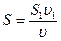Согласно уравнению Бернулли для сечений S и S₁,

,

где р и р₁ – статические давления жидкости соответственно для поверхности воды и отверстия; - плотность воды. Учитывая, что р₁=р (бак открыт), из выражения (2) 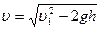. Подставив эту формулу в (1), найдём

(3)

Согласно кинематическим уравнениям 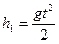и ℓ=υ₁t (t - время падения струи воды на Землю), найдём

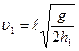. (4)

Подставив (4) в (3) и учитывая, что 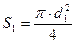, получаем искомую площадь сечения

Ответ: S=120см².

 

Пример 8.1. Водомер представляет собой горизонтальную трубу переменного сечения, в которую впаяны две вертикальные манометрические трубки одинакового сечения. По трубе протекает вода. Пренебрегая вязкостью воды, определите её массовый расход, если разность уровней в манометрических трубках Δh=8 см, а сечения трубы у оснований манометрических трубок соответственно равны S₁= 6см² и S₂=12см². Плотность воды ρ=1 г/см³.

Дано: Δh=8 см=0,08м; S₁= 6см²=6∙10^-4м²; S₂=12см² = 12∙10^-4м²;

ρ=1 г/см³=1∙10³ кг/м³.

Найти: Q.

Решение. Массовый расход воды- это масса воды, протекающая через сечение за единицу времени,

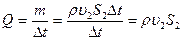(1)

где ρ – плотность воды; υ₂- скорость течения воды в месте сечения S₂. При стационарном течении идеальной несжимаемой жидкости выполняется уравнение неразрывности

S₁υ₁= S₂υ₂ (2)

и уравнение Бернулли для горизонтальной трубы (h₁=h₂)

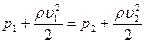(3)

где р₁ и р₂ – статические давления в сечениях манометрических трубок; υ₁ и υ ₂ - скорость течения воды в местах сечений S₁ и S₂. Учитывая, что

p₂-p₁=ρgΔh,

и решая систему уравнений (2), (3), получаем

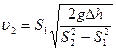
Подставив это выражение в (1), найдём искомый массовый расход воды:

Ответ: Q=0,868 кг/с.

 

Пример 8.1. Для определения объёма перекачки газа используется прибор, основанный на принципе действия трубки Пито (см. рисунок). При перекачке азота по трубе за время t =1мин проходит объём газа V=59,3м³. Определите диаметр трубы, если разность уровней воды в коленах трубки Пито Δh =1см. Плотность азота ρ =1,25 кг/м³, плотность воды ρ₁=1 г/см³.

Дано: t =1мин=60с; V=59,3м³; Δh =1см =1∙10^-2м; ρ =1,25 кг/м³;

ρ₁ =1 г/см³=1∙10³ кг/м³.

Найти: d.

Решение. Согласно уравнению Бернулли, разность давлений газа, оказываемых на колена трубки (см.рисунок),

(1)

где ρ – плотность газа; υ- скорость течения газа.

С другой стороны, разность давлений в коленах определяется разностью уровней жидкости в коленах трубки

Δр=ρ₁gΔh (2)

Приравняв выражения (1) и (2),

,

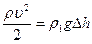Найдём скорость движения тела

(3)

Объём газа V, перекачиваемого за время t

V=Sυt

где S- площадь сечения трубы.

Подставляя в эту формулу выражение (3) и , найдём

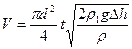
Откуда искомый диаметр трубы

Ответ: d=31,7 см.

 

Пример 8.1. Пренебрегая вязкостью воды, определите объём V воды в цилиндрическом баке диаметром d=1м, если через отверстие диаметром d₁=2см на дне бака вся вода вытекла за время t=30мин..

Дано: d=1м; t =30мин=1800с; d₁ =2см =2∙10^-2м.

Найти: V.

Решение. Если за время dt уровень воды в баке понижается на dh, то уменьшение объёма воды за это же время

dV=-Sdh, (1)

где S – площадь основания бака, а знак «-» указывает на то, что высота слоя воды уменьшается. С другой стороны уменьшение объёма воды за время dt

dV=S₁υdt, (2)

где S – площадь отверстия; υ - скорость истечения воды из отверстия, определяемая согласно формуле Торричелли (применима при S₁ << S),

(3)

где h – высота уровня воды в данный момент времени.

Приравняв выражение (1) и (2) и учитывая формулу (3), можем записать

,

откуда

.

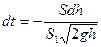Время вытекания всей воды из бака

(4)

где h₁ - первоначальный уровень воды. Из выражения (4)

(5)

Первоначальный объём воды

V=h₁S, (6)

Подставив в формулу (6) выражение (5), и учитывая, что 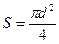, , 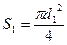найдём искомый объём воды

.

Ответ: V=2м³.

 

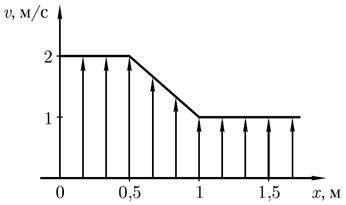
Пример 8.1. В области соприкосновения двух параллельно текущих слоёв воды их скорость изменяется, как показано на рисунке. Определите силу внутреннего трения F, если площадь S соприкосновения слоев равна 3м². Динамическая вязкость воды η=10^-3Па∙с.

Дано: S = 3м²; η=10^-3Па∙с.

Найти: F.

Решение. Сила внутреннего трения между слоями текущей жидкости

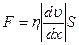, (1)

где η – динамическая вязкость жидкости; - градиент скорости; S - площадь соприкосновения слоёв.

Согласно заданному графику,

.

Подставляя значения физических величин в формулу (1), искомая сила внутреннего трения F=6∙10^-3Н.

Ответ: F=6 мН

 

Пример 8.1. Шарик радиусом r=2мм падает в глицерине с постоянной скоростью υ=8,5 мм/с. Определите число Рейнольдса Re и плотность ρ₁ материала шарика, если критическое число Рейнольдса Re_кр =0,5. Плотность глицерина ρ=1,26г/см³, динамическая вязкость глицерина η=1,48 Па∙с.

Дано: r=2мм =2∙10^-3 м; υ=8,5мм/с=8,5∙10^-3 м/с; Re_кр =0,5; η=1,48 Па∙с; ρ=1,26г/см³=1,26∙10³ кг/м³).

Найти: Re; ρ₁.

Решение. Характер течения жидкости зависит от числа Рейнольдса, определяемого формулой

,

где ρ– плотность жидкости; υ - скорость жидкости; d - диаметр шарика; η - динамическая вязкость жидкости. Учитывая данные задачи, получаем Re=0,029. Поскольку Re < Re_кр, то движение жидкости является ламинарным.

Стокс установил, что при небольших скоростях и размерах тел (при малых Re) сопротивление среды обусловлено практически только силой трения, определяемой по формуле

F=6πηrυ,

где r – радиус шарика.

При установившемся движении шарика в глицерине (υ=const) сила тяжести шарика (Р) уравновешивается выталкивающей силой (F_A) и силой трения (F):

P=F_A+F или

ρ₁gV =ρgV+6πηrυ (1)

где g – ускорение свободного падения; V- объём шарика. Подставив в уравнение (1) и решив его, найдём искомую плотность материала шарика:

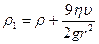
Ответ: Re=0,029; ρ₁=2,7 г/см³.

 

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: