 |
Подход на основе БПФ. Двухступенчатый Алгоритмический Подход. Алгоритм Расчёта Сдвига Частоты. Точная Компенсация Частотного Сдвига
|
|
|
|
Подход на основе БПФ
Самый простой подход к вычислению частоты состоит в том, чтобы вычислить БПФ входящего сигнала и определить пик. Это упрощённый подход, требующий выполнения традиционных алгоритмов. Однако существенным недостатком подхода на основе БПФ является значительное количество времени, требующегося для обработки. В результате он редко используется в коммерческих приложениях.
Двухступенчатый Алгоритмический Подход
Второй подход состоит в использовании двухступенчатого алгоритма вычисления частоты. На первой ступени приблизительно измеряется разница между ожидаемой частотой и наблюдаемой в приёмнике. На второй ступени применяется дополнительный алгоритм, чтобы обеспечить более точное определение. Этот подход используется в пакете Modulation toolkit среды LabVIEW и, поэтому, будет рассматриваться более подробно.
Алгоритм Расчёта Сдвига Частоты
Этап частотной компенсации может быть выполнен независимо от схемы модуляции. Цель этого этапа в процессе вычисления частоты состоит в том, чтобы компенсировать частотный сдвиг, действуя непосредственно на входной сигнал с комплексной огибающей. Математически мы можем представить модулированный сигнал с комплексной огибающей следующим уравнением:
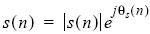
Более того, если произведена выборка с заданной частотой Fs, сигнал можно представить так:

Здесь θ v(n) представляет фазовую ошибку, которую порождает частотный сдвиг. Таким образом, в связи с тем, что результатом фазовой ошибки является изменение частоты, мы можем представить частотную ошибку как:
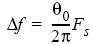
Fs представляет скорость выборки. Итак, чтобы компенсировать сдвиг частоты, мы должны применить смещение ∆ ƒ к нашему комплексному сигналу. Выполнив это, представим комплексный сигнал следующим уравнением:
|
|
|
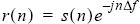
Точная Компенсация Частотного Сдвига
Для точной компенсации частотного сдвига потребуется несколько больше математических расчётов, при этом подход останется тем же. Как и раньше, мы представляем модулированный сигнал с комплексной огибающей следующим уравнением:
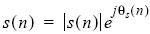
Уравнение можно дополнить, если сделать выборку с частотой передачи символов R. В результате получим следующее выражение:
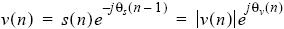
Здесь θ v(n-1) представляет абсолютную фазу предыдущего символа. На данном этапе применяется распознавание по максимальному правдоподобию, заданное следующим уравнением:

Откуда комплексный сигнал представляется в виде:

Если частоту выборки обозначить Fs, частотный сдвиг можно записать в следующем виде:
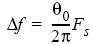
В результате сигнал с учетом выполненной компенсации частотного сдвига будет иметь следующее выражение:
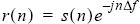
Определение Фазы
Поскольку теперь частотная ошибка системы вычислена, необходимо определить фазу несущей для восстановления символа. Существует две категории методов вычисления фазы: 1) методы, не управляемые решением (non-decision directed) и 2) методы, управляемые решением (decision directed).
Методы, неуправляемые решением
Два метода, которые мы будем рассматривать, это – фазовая автоподстройка частоты и алгоритм, называемый схемой Костаса (Costas loop – синфазно-квадратурная схема).
Фазовая автоподстройка частоты (Phase-Locked Loop – PLL) – алгоритм с обратной связью, позволяющий приёмнику синхронизироваться с фазой принятого сигнала. Для этого вначале необходимо вычислить фазу сигнала и затем подстроить собственную фазу приемника. При каждой итерации измеряется фазовая ошибка полученного сигнала, которая используется для пропорционального регулирования сдвига фазы на следующем повторении. В результате приёмник за какое-то время (overtime) может точно захваттть фазу передатчика.
|
|
|
Цикл Коста похож на PLL, однако в нём используется двухфазовые детекторы для измерения фазы принятого сигнала. Выход каждого из этих детекторов проходит через фильтр нижних частот и подается на вход другого фазового детектора, который используется для управления гетеродином. Он позволяет пропорционально регулировать фазу для следующего повторения. Цикл Коста – это рекурсивный алгоритм, при помощи которого приёмник может точно синхронизироваться с передатчиком через какой-то промежуток времени.
Методы, управляемые решением
Имеется несколько методов, управляемых решением, для восстановления фазы. Эти методы включают цикл обратной связи, управляемый решением, метод минимума среднеквадратичной ошибки и детектирование по критерию максимального правдоподобия. В данном разделе мы сфокусируемся на механизме детектирования по критерию максимального правдоподобия, применяемом в пакете Modulation toolkit.
|
|
|


