 |
Основы Фильтрации. фильтр с косинусоидальным сглаживанием Нет фильтрации. Скорость передачи символов и Ширина полосы
|
|
|
|
Основы Фильтрации
До настоящего момента мы рассматривали модуляцию несущего сигнала без фильтрации, чтобы проиллюстрировать понятие скорости передачи символов. Однако если посмотреть на необработанный модулированный сигнал, видна необходимость фильтрации. Как видно на приведённом ниже рисунке, в таком сигнале содержатся резкие изменения фазы и амплитуды. Несмотря на то, что такое поведение не влияет на качество демодуляции, резкие переходы являются причиной наличия высокочастотных компонентов в спектре сигнала.




|

В результате, если не используется фильтрация, резкие переходы являются причиной помех, возникающих за пределами выделенной полосы канала. Эти помехи могут попадать в полосы смежных каналов и являться причиной межсимвольной интерференции (ISI). В результате, ISI можно уменьшить двумя способами, с передающей стороны при помощи формирующего (pulse-shaped) фильтра, и со стороны приёмника при помощи согласованного фильтра.
Ниже показан сигнал во временной области, к которому применена формирующая фильтрация. Как показано на этом рисунке, теперь переходы фазы и амплитуды происходят намного более гладко.


|

Кроме того, результат сглаживания можно ясно увидеть в частотной области обоих сигналов, что показано ниже:
фильтр с косинусоидальным сглаживанием Нет фильтрации

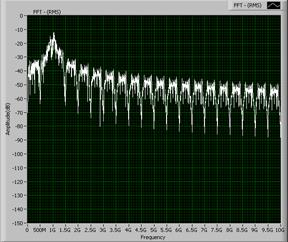
 (Raised Cosine Filter Alpha = 0. 5)
(Raised Cosine Filter Alpha = 0. 5)
Итак, мы видим, насколько полезна фильтрация для уменьшения ширины канала. Однако в этой демонстрации мы больше сконцентрируемся на установлении взаимосвязи между скоростью передачи символов и шириной полосы канала.
|
|
|
Скорость передачи символов и Ширина полосы
Как уже упоминалось, скорость передачи символов прямо пропорциональна ширине полосы канала. Фактически, ширина полосы канала определяется уравнением:
Bw = Rs (1 + α )
В данном уравнении ‘Bw’ – это ширина полосы канала, ‘Rs’ –скорость передачи символов, ‘α ’ – параметр фильтра. Ниже показано АЧХ канала с высокой скоростью передачи символов. Обратите внимание, что для формирования канала применялся фильтр с косинусоидальным сглаживанием (α = 0. 5). Частота несущей равна 1 ГГц, скорость передачи символов – 500 МГц. Согласно нашему уравнению, ширина полосы канала тогда станет 500 МГц * (1. 5) = 750 МГц. С центральной частотой 1 ГГц канал будет занимать полосу от 650 МГц до 1350 МГц.




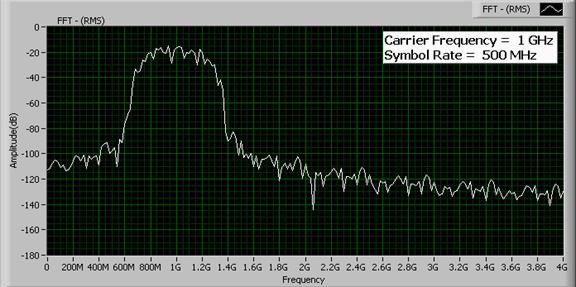
Теперь покажем ту же систему, только скорость передачи символов равна 100 МГц. В результате ширина полосы канала равна одной пятой от исходной. Таким образом, при α = 0. 5 ширина полосы равна:
Bw = 100 МГц (1 + 0. 5) = 150 МГц
С центральной частотой 1 ГГц канал будет занимать полосу от 925 МГц до 1075 МГц. АЧХ канала приведена ниже.



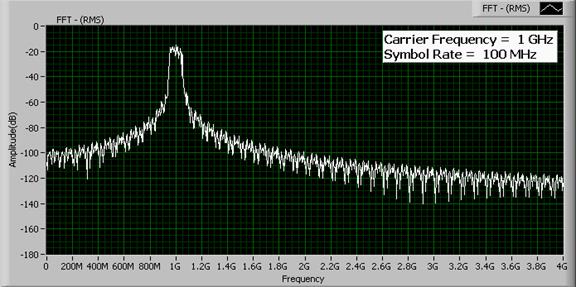
Два графика иллюстрируют взаимосвязь между скоростью передачи символов и шириной канала, демонстрируя, что ширина полосы канала увеличивается с увеличением скорости передачи символов. Итак, для максимального увеличения числа каналов в заданной частотной области необходимо использовать низкую скорость передачи символов. Однако это приводит к уменьшению пропускной способности канала. Таким образом, существует компромисс между скоростью передачи символов (и отсюда пропускной способностью канала) и требуемой шириной полосы канала.
|
|
|


