 |
Методы Максимального Правдоподобия (MT Max Eye)
|
|
|
|
Методы Максимального Правдоподобия (MT Max Eye)
Одним из подходов к осуществлению синхронизации символа в пакете LabVIEW Modulation toolkit является метод Max Eye (Максимального правдоподобия). При использовании этого метода оптимальный дискретный сдвиг вычисляется посредством выбора такого сдвига, который приводит к максимуму открытие глазковой диаграммы. Однако этот метод восприимчив к шуму в канале, который закрывает глазковую диаграмму. Поэтому в случаях, когда речь идёт о значительном шуме в канале связи, осуществление точного восстановления несущей крайне затруднительно.
Ошибка Частоты
Как уже упоминалось, восстановление несущей важно для восстановления информации о частоте и фазе передаваемого сигнала. Для того чтобы показать важность восстановления несущей, сначала покажем схему «созвездие» сигнала, в котором частота не вычислена должным образом. Это можно сделать в LabVIEW путём введения значительной частотной ошибки с помощью ВП Add Phase Noise (Добавить Фазовый Шум). Из-за частотной ошибки можно наблюдать (справа) кольцевой рисунок, показывающий, что схема «созвездие» вращается. Такое поведение свидетельствует о том, что демодулятор не способен восстановить нужную информацию о частоте передаваемого сигнала.
Фазовая Ошибка
Вторая важная характеристика восстановления несущей – это корректировка фазовой ошибки. На рисунке справа смоделировано возникновение именно фазовой ошибки, так как каждый из символов повторно попадает в одну и ту же область. Это показывает, что мы правильно вычислили частоту несущей. В противном случае схема «созвездие» стала бы вращаться. Однако области имеют одинаково сдвинутые фазы по сравнению с идеальной символьной картой. Таким образом, мы можем определить, что PLL всё ещё имеет небольшой фазовый сдвиг от несущего сигнала.
|
|
|
Влияние Шума на Восстановление Несущей
По существу, шум в канале больше всего осложняет распознавание информации о частоте и фазе передаваемого сигнала. Из-за этого, вы часто будете видеть, что схема «созвездие» начинает вращаться при увеличении уровня шума. В нормальных условиях механизм восстановления несущей достаточно устойчив и позволяет вычислить небольшую фазовую и частотную ошибку. Однако в экстремальных обстоятельствах даже при использовании лучших алгоритмических подходов невозможно точно дешифровать эту информацию.
Демонстрация
В следующем примере мы рассмотрим влияние белого гауссовского шума на восстановление несущей. Более подробно мы рассмотрим, что может случиться, если шум в канале достаточен, чтобы помешать захвату несущей. Для демонстрации этого следуйте шагам, описанным ниже:
1) Запустите демонстрацию QAM модуляции и выберите схему 16-QAM. Когда появится запрос файла, выберите “smiley_tiny (recommended).jpg. ” Данная демонстрация открывает JPG файл, затем конвертирует его в поток битов, который модулирует, используя схему QAM модуляции, и далее выполняет обратный процесс для восстановления исходного изображения. По умолчанию отношение сигнал/шум в канале установлено на максимальное значение, так что схема «созвездие» показывает символы, почти идеально находящиеся на своих позициях. Это говорит о том, что при каждом повторении и фазу, и частоту несущей можно правильно определить. Поэтому изображение, предназначенное для передачи («Image to Modulate»), и демодулированное изображение («Demodulated Image») очень похожи друг на друга. Вид лицевой панели этого ВП показан ниже:
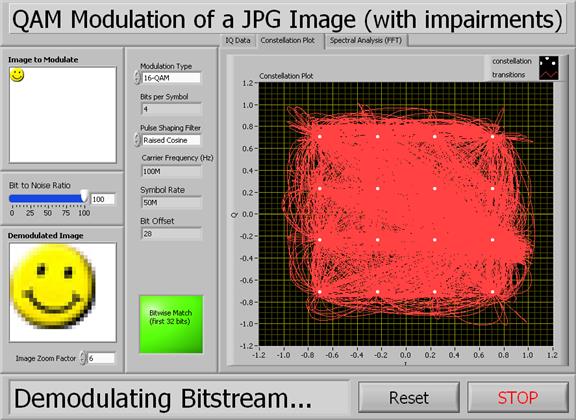
2) Теперь медленно уменьшайте отношение сигнал/шум (Bit to Noise Ratio)” и наблюдайте за изменением схемы «созвездие». Фактически, когда это отношение уменьшается, уровень шума возрастает. В результате восстановленные символы начинают дрожать, чем отличаются от идеально расположенных символов. Как показывает схема «созвездие», шума достаточно, чтобы быть причиной некоторого дрожания каждого места расположения символа. Однако каждый из этих символов всё ещё может отображаться в правильном битовом значении. Таким образом, изображение восстановлено корректно.
|
|
|
3) Теперь рассмотрим восстановление частоты, выполняемое при помощи PLL, при добавлении шума в количестве достаточном, чтобы информация о фазе и частоте несущего сигнала не могла быть определена. Для этого значение “Bit to Noise Ratio” должно быть установлено примерно на 30 (используя 16-QAM). Медленно начинаем уменьшать это значение, пока схема «созвездие» не начнёт вращаться, как показано на диаграмме внизу. Эта диаграмма иллюстрирует две ключевые особенности. Во-первых, обратите внимание, что демодулированное изображение восстановлено неточно и имеет некоторое сходство с исходным изображением. Это показывает, что, по меньшей мере, некоторые из символов расположены в местах, которые близки к ожидаемым. Во-вторых, и это более важно, заметьте, что схема «созвездие» сейчас имеет кольцевой вид или вид, похожий на мишень. Визуально это говорит нам о том, что схема «созвездие» сейчас вращается и что частота несущей не может быть должным образом определена.
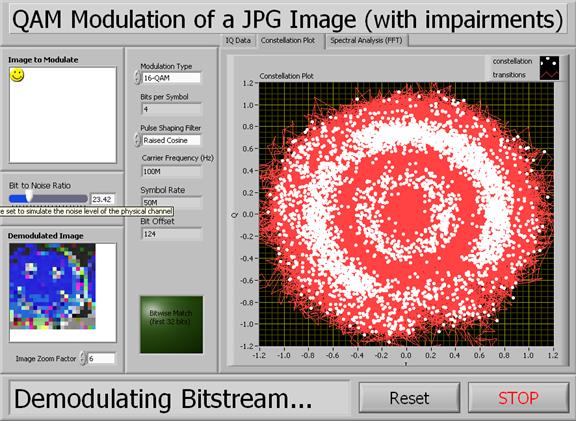
4) Теперь мы попытаемся «сломать» обратное преобразование путём добавления такого количества шума, что PLL вообще не сможет восстановить исходную фазу и частоту несущей. Вспомните, что PLL – это петля обратной связи. Поэтому определение фазы и частоты таким образом, при котором они сильно отличаются от ожидаемых значений, может стать причиной серьёзных трудностей. Уменьшите “Bit to Noise Ratio” до 0. Как вы можете видеть на схеме “созвездие» (см. внизу), каждый символ из-за шума в канале появляется практически в случайном месте.
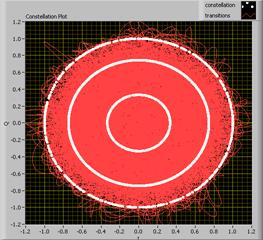
5) Удерживайте уровень шума на максимуме в течение, по меньшей мере, пятнадцати итераций цикла. Таким образом мы дезориентируем PLL, поскольку задаём значения фазы и частоты, которые очень отличаются от ожидаемых. Поэтому, даже если шум удаляется из канала, PLL не может восстановить начальную фазу и амплитуду.
|
|
|
6) Теперь удалите весь шум из канала, изменяя “Bit to Noise Ratio” до 100. Как вы можете видеть на схеме «созвездие» справа, символы не могут отображаться на своих идеальных позициях, так как PLL неправильно вычисляет фазу и частоту. Итак, схема «созвездие» начинает вращаться. При некоторых обстоятельствах PLL после нескольких повторений начнет работать. Однако, как правило, мы должны перезапустить ВП преобразования с понижением частоты, чтобы PLL смогла опять захватить несущую.
7) Наконец, проведём опыт с количеством итераций, которые выполняет PLL при максимальном шуме до его устранения из физического канала. Вы заметите, что в некоторых случаях схема «созвездие» сначала как будто показывает значительное дрожание, однако затем устанавливаются соответствующие фаза и амплитуда. Справа показан вид схемы «созвездие», когда PLL почти захватила частоту несущей. Здесь символы расположены близко к их идеальным местам, но каждый символ последовательно сдвинут по кругу. В этом особом случае PLL полностью захватывает фазу и частоту несущей на последующих итерациях.
|
|
|
