Классификация шифров замены

 

Если ключ зашифрования совпадает с ключом расшифрования: k ₃ = k_p, то такие шифры называют симметричными, если же k ₃ 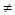k_р — асимметричными.

В связи с указанным различием в использовании ключей сделаем еще один шаг в классификации:

 

Отметим также, что в приведенном определении правило зашифрования Е_k (х) является, вообще говоря, многозначной функцией. Выбор ее значений представляет собой некоторую проблему, которая делает многозначные функции Е_k(х) не слишком удобными для использования. Избавиться от этой проблемы позволяет использование однозначных функций, что приводит к естественному разделению всех шифров замены на однозначные и многозначные замены (называемых также в литературе омофонами).

Для однозначных шифров замены справедливо свойство:

 

 

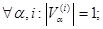
для многозначных шифров замены:

 

 

 

Исторически известный шифр — пропорциональной замены представляет собой пример шифра многозначной замены, шифр гаммирования - пример шифра однозначной замены. Далее мы будем заниматься в основном изучением однозначных замен, получивших наибольшее практическое применение. Итак, далее М = N и .

Заметим, что правило зашифрования Е_k естественным образом индуцирует отображение , которое в свою очередь продолжается до отображения . Для упрощения записи будем использовать одно обозначение Е_k для каждого из трех указанных отображений.

В силу инъективности (по k)отображения Е_k и того, что | U| = |V|, введенные в общем случае отображения   являются биекциями , определенными равенствами

 

.

Число таких биекций не превосходит N!.

Для шифра однозначной замены определение правила зашифрования можно уточнить: в формуле включение следует заменить равенством

 

 

Введем еще ряд определений.

Если для некоторого числа q N выполняются включения v_i В^q, i =1 ,N, то соответствующий шифр замены будем называть шифром равнозначной замены. В противном случае — шифром разнозначной замены:

 

В подавляющем большинстве случаев используются шифры замены, для которых U А^р, для некоторого р N. При р = 1 говорят о поточных шифрах замены, при р > 1 — о блочных шифрах замены:

 

 

Следующее определение. В случае r= 1 шифр замены называют одноалфавитным шифром замены или шифром простой замены. В противном случае – многоалфавитным шифром замены:

 

Ограничиваясь наиболее важными классами шифров замены и исторически известными классами шифров перестановки, сведем результаты классификации в схему, изображенную на рисунке.

Одноалфавитные шифры

 

Следует подчеркнуть, что стрелки, выходящие из любого прямоугольника схемы, указывают лишь на наиболее значимые частные подклассы шифров. Пунктирные стрелки, ведущие из подклассов шифров перестановки, означают, что эти шифры можно рассматривать и как блочные шифры замены в соответствии с тем, что открытый текст делится при шифровании на блоки фиксированной длины, в каждом из которых производится некоторая перестановка букв. Одноалфавитные и многоалфавитные шифры могут быть как поточными, так и блочными. В то же время шифры гаммирования, образующие подкласс многоалфавитных шифров, относятся к поточным, а не к блочным шифрам. Кроме того, они являются симметричными, а не асимметричными шифрами.

Шифр Виженера

Наиболее известными являются шифры замены, или подстановки, особенностью которых является замена символов (или слов, или других частей сообщения) открытого текста соответствующими символами, принадлежащими алфавиту шифротекста. Различают одноалфавитную и многоалфавитную замену. Вскрытие одноалфавитных шифров основано на учете частоты появления отдельных букв или их сочетаний (биграмм, триграмм и т. п.) в данном языке. Классические примеры вскрытия таких шифров содержатся в рассказах Э. По "Золотой жук" и А.Конан Дойля "Пляшущие человечки".

Примером многоалфавитного шифра замены является так называемая система Виженера. Шифрование осуществляется по таблице, представляющей собой квадратную матрицу размерностью п X n, где п - число символов используемого алфавита. На рис.4 показана таблица Виженера для русского языка (алфавит Z₃₂- 32 буквы и пробел). Первая строка содержит все символы алфавита. Каждая следующая строка получается из предыдущей циклическим сдвигом последней на символ влево.

 

Рисунок 4.Таблица Виженера для алфавита Z₃₂

Выбирается ключ или ключевая фраза. После чего процесс зашифрования осуществляется следующим образом. Под каждой буквой исходного сообщения последовательно записываются буквы ключа; если ключ оказался короче сообщения, его используют несколько раз. Каждая буква шифротекста находится на пересечении столбца таблицы, определяемого буквой открытого текста, и строки, определяемой буквой ключа. Пусть, например, требуется зашифровать сообщение:

 

ГРУЗИТЕ АПЕЛЬСИНЫ БОЧКАМИ ТЧК БРАТЬЯ КАРАМАЗОВЫ ТЧК

 

С помощью ключа ВЕНТИЛЬ запишем строку исходного текста с расположенной под ней строкой с циклически повторяемым ключом:

 

ГРУЗИТЕ АПЕЛЬСИНЫ БОЧКАМИ ТЧК БРАТЬЯ КАРАМАЗОВЫ ТЧК

 

ВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕНТИЛЬВЕ

 

В результате зашифрования, начальный этап которого показан на рисунке 5, получим шифротекст:

 

ЕХЩРЭАБЕЫЧУДККТИСЙЩРМЕЩЬЗЭРМДОБИЭУАДЧТШЛЕВМЪФГКЛЩП

Рисунок 5. Принцип шифрования по таблице Виженера

 

Расшифрование осуществляется следующим образом. Под буквами шифро-текста последовательно записываются буквы ключа; в строке таблицы, соответствующей очередной букве ключа, происходит поиск соответствующей буквы шифротекста. Находящаяся над ней в первой строке таблицы буква является соответствующей буквой исходного текста.

Для увеличения надежности шифра можно рекомендовать его использование после предварительной псевдослучайной перестановки букв в каждой строке таблицы. Возможны и другие модификации метода.

II. Советы по выполнению частотного анализа английских текстов

 

(1)Начните с подсчета частоты появления каждой из букв шифр-текста. Примерно пять букв должны появляться с частотой менее 1 процента, и они вероятно, представляют собой j, k, q, х и z. Одна из букв должна появляться с частотой более 10 процентов, и она, по-видимому, представляет собой е. Если шифр-текст не подчиняется этому распределению частот, то, возможно, исходное сообщение написано не на английском языке. Вы можете определить, какой это язык, если проанализируете частотное распределение букв в шифр-тексте. К примеру, в итальянском языке обычно ecть, три буквы с частотностью более 10 процентов и 9 букв с частотностью менее 1 процента. В немецком языке буква е имеет чрезвычайно высокую частотность – 19 процентов, поэтому любой шифр-текст, в котором одни из букв встречается столь же часто, является, вполне возможно, немецким. После того как вы определили язык, для выполнения частотного анализа вам следует воспользоваться соответствующей таблицей частотности букв для данного языка. Если у вас есть нужная таблица частотности букв, то нередко удается дешифровать даже шифр-тексты на неизвестном языке.

(2)Если установлена взаимосвязь с английским языком, но, как часто и происходит, сразу же открытый текст не появляется, тогда обратите внимание на пары повторяющихся букв. В английском языке чаще всего повторяющимися буквами будут ss, ее, tt, ff, 11, mm и оо. Если в шифр-тексте имеются какие-либо повторяющиеся символы, то вы можете считать, что они представляют собой одну из этих пар.

(3)Если в шифр-тексте имеются пробелы между словами, то постарайтесь определить слова, состоящие из одной, двух или трех букв. Единственными словами в английском языке, состоящими из одной буквы, являются а и I. Чаще всего встречающимися двухбуквенными словами будут of, to, in, it, is, be, as, at, so, we, he, by, or, on, do, if, me, my, up, an, go, no, us, am. Наиболее часто появляющиеся трехбуквенные слова – the и and.

(4)Если удастся, подготовьте таблицу частотности букв для сообщения, которое вы стараетесь дешифровать. Например, в военных донесениях стремятся опускать местоимения и артикли, и отсутствие таких слов, как I, he, а и the, будет снижать частотность некоторых из чаще всего встречающихся букв. Если вы знаете, что работаете с военным донесением, вам следует использовать таблицу частотности букв, созданную на основе других военных донесений.

(5) Одно из самых полезных для криптоаналитика умений – это способность благодаря собственному опыту или чисто интуитивно – распознавать слова или даже целые фразы. Аль-Халил, один из первых арабских криптоаналитиков, продемонстрировал свои способности, когда взломал греческий шифр-текст. Он предположил, что шифр-текст начинается с приветствия «Во имя бога». Установив, что эти буквы соответствуют определенному фрагменту шифр-текста, он смог использовать их в качестве лома и раскрыть остальной шифр-текст. Это получило название криб.

(6) В некоторых случаях наиболее часто встречающейся буквой в шифр-тексте может быть Е, следующей по частоте появления – Т и так далее. Другими словами, частотность букв в шифр-тексте уже совпадает с частотностью букв в таблице. По-видимому, буква Е в шифр-тексте является действительно е, и то же самое, похоже, справедливо и для других букв, и все же шифр-текст выглядит тарабарщиной. В этом случае вы столкнулись не с шифром замены, а с шифром перестановки. Все буквы остались теми же самыми, но находятся они не на своих местах.

III. Задания на криптоанализ классических шифров

 

3.1 Шифр столбцовой перестановки

 

При решении заданий на криптоанализ шифров перестановки необходимо восстановить начальный порядок следования букв текста. Для этого используется анализ совместимости символов, в чем может помочь таблица сочетаемости.

 

Таблица 1. Сочетаемость букв русского языка

Г	С	Слева		Справа	Г	С
3	97	л, д, к, т, в, р, н	А	л, н, с, т, р, в, к, м	12	88
80	20	я, е, у, и, а, о	Б	о, ы, е, а, р, у	81	19
68	32	я, т, а, е, и, о	В	о, а, и, ы, с, н, л, р	60	40
78	22	р, у, а, и, е, о	Г	о, а, р, л, и, в	69	31
72	28	р, я, у, а, и, е, о	д	е, а, и, о, н, у, р, в	68	32
19	81	м, и, л, д, т, р, н	Е	н, т, р, с, л, в, м, и	12	88
83	17	р, е, и, а, у, о	Ж	е, и, д, а, н	71	29
89	11	о, е, а, и	3	а, н, в, о, м, д	51	49
27	73	р, т, м, и, о, л, н	и	с, н, в, и, е, м, к, з	25	75
55	45	ь, в, е, о, а, и, с	к	о, а, и, р, у, т, л, е	73	27
77	23	г, в, ы, и, е, о, а	л	и, е, о, а, ь, я, ю, у	75	25
80	20	я, ы, а, и, е, о	м	и, е, о, у, а, н, п, ы	73	27
55	45	д, ь, н, о, а, и, е	н	о, а, и, е, ы, н, у	80	20
11	89	р, п, к, в, т, н	о	в, с, т, р, и, д, н, м	15	85
65	35	в, с, у, а, и, е, о	п	о, р, е, а, у, и, л	68	32
55	45	и, к, т, а, п, о, е	р	а, е, о, и, у, я,ы, н	80	20
69	31	с, т, в, а, е, и, о	с	т, к, о, я, е, ь, с, н	32	68
57	43	ч, у, и, а, е, о, с	т	о, а, е, и, ь, в, р, с	63	37
15	85	п, т, к, д, н, м, р	У	т, п, с, д, н, ю, ж	16	84
70	30	н, а, е, о, и	ф	и, е, о, а, е, о, а	81	19
90	10	у, е, о, а, ы, и	X	о, и, с, н, в, п, р	43	57
69	31	е, ю, н, а, и	ц	и, е, а, ы	93	7
82	18	е, а, у, и, о	ч	е, и, т, н	66	34
67	33	ь, у, ы, е, о, а, и, в	ш	е, и, н, а, о, л	68	32
84	16	е, б, а, я, ю	щ	е, и, а	97	3
0	100	м, р, т, с, б, в, н	ы	л, х, е, м, и, в, с, н	56	44
0	100	н, с, т, л	ь	н, к, в, п, с, е, о, и	24	76
14	86	с, ы, м, л, д, т, р, н	э	н, т, р, с, к	0	100
58	42	ь, о, а, и, л, у	ю	д, т, щ, ц, н, п	11	89
43	57	о, н, р, л, а, и, с	я	в, с, т, п, д, к, м, л	16	84

 

Таблица 2. Сочетаемость букв английского языка

Г	С	Слева		Справа	Г	С
19	81	l,c,d,m,n,s,w,t,r,e,h	A	n,t,s,r,l,d,c,m	6	94
55	45	y,b,n,t,u,d,o,s,a,e	В	e,l,u,o,a,y,b,r	70	30
61	39	u,o,s,n,a,i,l,e	С	h,o,e,a,i,t,r,l,k	59	41
52	48	r,i,l,a,n,e	D	e,i,t,a,o,u	54	46
8	92	c,b,e,m,v,d,s,l,n,t,r,h	E	r,d,s,n,a,t,m,e,c,o	21	79
69	31	s,n,f,d,a,i,e,o	F	t,o,e,i,a,r,f,u	52	48
36	64	o,d,u,r,i,e,a,n	G	e.h.o.r.a.t.f.w.i.s	42	58
7	93	g,e,w,s,c,t	H	e,a,i,o	90	10
13	87	f,m,w,e,n,l,d,s,r,h,t	I	n,t,s,o,c,r,e,m,a,l	17	83
28	72	y,w,t,s,n,e,c,b,a,c	J	u,o,a,e,m,w	88	12
53	47	y,u,i,n,a,r,o,c	К	e,i,n,a,t,s	68	32
52	48	m,p,t,i,b,u,o,e,l,a	L	e,i,y,o,a,d,u	65	35
69	31	s,d,m,r,i,a,o,e	M	e,a,o,i,p,m	71	29
89	11	u,e,o,a,i	N	d,t,g,e,a,s,o,i,c	32	68
21	79	o,d,l,p,h,n,e,c,f,s,i,r,t	о	n,f,r,u,t,m,l,s,w,o	18	82
47	53	r,l,t,n,i,p,m,a,o,u,e,s	P	o,e,a,r,l,u,p,t,i,s	59	41
20	80	o,n,l,e,d,r,s	Q	u	100	0
70	30	p,i,u,t,a,o,e	R	e,o,a,t,i,s,y	61	39
48	52	d,t,o,u,r,n,s,i,a,e	S	t,e,o,i,s,a,h,p,u	41	59
43	57	u,o,d,t,f,e,i,n,s.a	Т	h,i,o,e,a,t,r	38	62
35	65	p,f,t,l,b,d,s,o	и	n,s,t,r,l,p,b,c	8	92
88	12	r,u,o,a,i,e	V	e,i,o,a	99	1
48	52	g,d,y,n,s,t,o,e	w	a,h,i,e,o,n	80	20
95	5	u,n,i,e	X	p,t,i,a,u,c,k,o	38	62
24	76	b,n,a,t,e,r,l	Y	a,o,s,t,w,h,i,e,d,m	38	62
88	12	o,n,a,i	z	e,i,w	86	14

 

При анализе сочетаемости букв друг с другом следует иметь в виду зависимость появления букв в открытом тексте от значительного числа предшествующих букв. Для анализа этих закономерностей используют понятие условной вероятности.

Систематически вопрос о зависимости букв алфавита в открытом тексте от предыдущих букв исследовался известным русским математиком А.А.Марковым (1856 — 1922). Он доказал, что появления букв в открытом тексте нельзя считать независимыми друг от друга. В связи с этим А. А. Марковым отмечена еще одна устойчивая закономерность открытых текстов, связанная с чередованием гласных и согласных букв. Им были подсчитаны частоты встречаемости биграмм вида гласная-гласная (г,г), гласная-согласная (г,с), согласная-гласная (с,г), согласная-согласная (с,с) в русском тексте длиной в 10⁵ знаков. Результаты подсчета отражены в следующей таблице:

 

Таблица 3. Чередование гласных и согласных

	Г	С	Всего
Г	6588	38310	44898
С	38296	16806	55102

 

Пример решения:

Дан шифр-текст: СВПООЗЛУЙЬСТЬ_ЕДПСОКОКАЙЗО

Текст содержит 25 символов, что позволяет записать его в квадратную матрицу 5х5. Известно, что шифрование производилось по столбцам, следовательно, расшифрование следует проводить, меняя порядок столбцов.

 

С	В	П	О	О
З	Л	У	Й	Ь
С	Т	Ь	_	Е
Д	П	С	О	К
К	А	Й	З	О

 

Необходимо произвести анализ совместимости символов (Таблица сочетаемости букв русского и английского алфавита, а также таблицы частот биграмм представлена выше). В первом и третьем столбце сочетание СП является крайне маловероятным для русского языка, следовательно, такая последовательность столбцов быть не может. Рассмотрим другие запрещенные и маловероятные сочетания букв: ВП (2,3 столбцы), ПС (3,1 столбцы), ПВ (3,2 столбцы). Перебрав их все, получаем наиболее вероятные сочетания биграмм по столбцам:

 

В	О	С	П	О
Л	Ь	З	У	Й
Т	Е	С	Ь	_
П	О	Д	С	К
А	З	К	О	Й

 

Получаем осмысленный текст: ВОСПОЛЬЗУЙТЕСЬ_ПОДСКАЗКОЙ

Предыдущая12345678Следующая

Поделиться:

Воспользуйтесь поиском по сайту: