Теория криптоанализа шифра Виженера

 

Рассмотрим шифр модульного гаммирования с уравнением b_i = (a_i+ y_i) mod n, для которого гамма является периодической последовательностью знаков алфавита. Такая гамма обычно получается периодическим повторением некоторого ключевого слова. Например, ключевое слово KEY дает гамму KEYKEYKEY.... Рассмотрим задачу вскрытия такого шифра по тексту одной криптограммы достаточной длины.

Пусть µ - длина ключевого слова. Обычно криптоанализ шифра Виженера проводится в два этапа. На первом этапе определяется число µ, на втором этапе — само ключевое слово.

Для определения числа µ применяется так называемый тест Казиски, названный в честь Ф. Казиски, применившего его в 1863 г. Тест основан на простом наблюдении о том, что два одинаковых отрезка открытого текста, отстоящих друг от друга на расстоянии, кратном µ, будут одинаково зашифрованы. В силу этого в шифр-тексте ищутся повторения длины, не меньшей трех, и расстояния между ними. Обратим внимание на то, что случайно такие одинаковые отрезки могут появиться в тексте с достаточно малой вероятностью.

Пусть d₁,d₂,... — найденные расстояния между повторениями и d — наибольший общий делитель этих чисел. Тогда µ должно делить d. Чем больше повторений имеет текст, тем более вероятно, что µ совпадает с d. Для уточнения значения µ, можно использовать так называемый индекс совпадения, введенный в практику У. Фридманом в 1920 г.

Для строки х = (x₁,...,_,x_m) длины т, составленной из букв алфавита А, индексом совпадения в х, обозначаемым I_c(х) будем называть вероятность того, что две случайно выбранные буквы из х совпадают.

Пусть A = { a_i,..., a_n }. Будем отождествлять буквы алфавита с числами, гак что

 

a₁ ≡ 0,..., a_n-1 ≡ n - 2, а_n = n -1.

 

Теорема. Индекс совпадения в х вычисляется по формуле

 

 (1)

 

где f_i — число вхождений буквы a_i в х, i  Z_n.

Доказательство. Будем вычислять I_с(х) как отношение числа благоприятных исходов к общему числу исходов. Благоприятным является исход, при котором на выбранных двух позициях в х расположены одинаковые буквы. Общее число исходов равно, очевидно, С²_m. Число благоприятных исходов есть

 

, (2)

 

В самом деле, переупорядочим буквы в х таким образом, чтобы сначала шли f_a1 букв а₁ затем — f_a2букв а₂ и т.д.(4):

 

, (3)

 

Теперь заметим, что при случайном выборе мест (i и j) в строке х благоприятными являются следующие исходы:

 

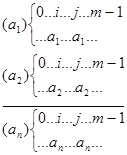
В случае (а₁) мы можем выбрать пару букв а, из набора (3) способами, в случае (а₂) пару букв а₂ из (3) — способами и т. д.

Таким образом, общее число благоприятных исходов выражается величиной (2), а индекс совпадения в х — формулой

 

 

и, следовательно, формулой (1).

Пусть х — строка осмысленного текста (например, английского). Допустим, как и ранее, что буквы в х появляются на любом месте текста с соответствующими вероятностями р₀,...,р_n-1 независимо друг от друга, где р_i — вероятность появления буквы i в осмысленном тексте, i  Z_n В такой модели открытого текста вероятность того, что две случайно выбранные буквы из х совпадают с i  Z_n равна p²_i следовательно,

 

, (4)

 

Взяв за основу значения вероятностей р_i для открытых текстов на английском языке, получаем приближение . Тем самым для английских текстов х можно пользоваться следующим приближением для индекса совпадения:

I_с(x) ≈ 0,066.

 

Аналогичные приближения можно получить и для других языков. Так, для русского языка получаем приближение:

I_с(x) ≈ 0,053.

 

Приведем значения индексов совпадения для ряда европейских языков:

 

Таблица 7. Индексы совпадения европейских языков

Язык	Русский	Алгл.	Франц.	Нем.	Итал.	Испан.
	0,0529	0,0662	0,0778	0,0762	0,0738	0,0775

 

Рассуждения, использованные при выводе формулы (4), остаются, очевидно, справедливыми и в случае, когда х результат зашифрования некоторого открытого текста простой заменой. В этом случае вероятности р_i переставляются местами, но сумма  остается неизменной.

Предположим, что х — реализация независимых испытаний случайной величины, имеющей равномерное распределение на Z _n. Тогда индекс совпадения вычисляется по формуле

 

 

Вернемся к вопросу об определении числа µ.

Пусть y = y₁ y ₂ …y _n — данный шифр-текст. Выпишем его с периодом µ:

 

и обозначим столбцы получившейся таблицы через Y^↓₁,..., Y^↓_µ. Если µ это истинная длина ключевого слова, то каждый столбец Y^↓_i, i 1, µ, представляет собой участок открытого текста, зашифрованный простой заменой, определяемой подстановкой

 

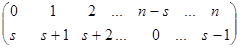 (5)

 

для некоторого s 0,n-l (числа берутся по модулю n).

В силу сказанного выше, (для английского языка) I_с(Y^↓_i) ≈ 0,066 при любом i. С другой стороны, если µ отлично от длины ключевого слова, то столбцы Y^↓_i будут более "случайными", поскольку они являются результатом зашифрования фрагментов открытого текста некоторым многоалфавитным шифром. Тогда I_с(Y^↓_i) будет ближе (для английского языка) к числу1/28 ≈ 0,038

Заметная разница значений I_с(x) для осмысленных открытых текстов и случайных последовательностей букв (для английского языка — 0,066 и 0,038, для русского языка — 0,053 и 0,030) позволяет в большинстве случаев установить точное значение µ.

Предположим, что на первом этапе мы нашли длину ключевого слова µ. Рассмотрим теперь вопрос о нахождении самого ключевого слова. Для его нахождения можно использовать так называемый взаимный индекс совпадения.

Пусть х = (х_],...,х_п),у = (у₁,...,у_т) — две строки букв алфавита А. Взаимным индексом совпадения х и у, обозначаемым МI_с(х, у), называется вероятность того, что случайно выбранная буква из х совпадает со случайно выбранной буквой из у.

Пусть f₀ f₁ …f_n и f¹₀ f¹₁ … f¹_n-1 — числа вхождений букв алфавита в х и у

соответственно.

Теорема. Взаимный индекс совпадения в х и у вычисляется по формуле (эта теорема доказывается точно так же, как и предыдущая теорема.)

, (6)

 

Пусть k = (k₁,..., k_µ,) — истинное ключевое слово. Попытаемся оценить индексы MI_c(Y^↓_i, Y^↓_j)

Для этого напомним, что Y^↓₃ является результатом зашифрования фрагмента открытого текста простой заменой, определяемой подстановкой (5) при некотором s. Вероятность того, что Y^↓_i и Y^↓_j произвольная пара букв равна 0, имеет вид p_n-si*p_n-sj (где р_а — вероятность появления буквы а в открытом тексте); вероятность того, что обе буквы есть 1, равна p_n-si+1*p_n-sj+1 и так далее. На основании этого получаем:

 

 

Заметим, что сумма в правой части последнего равенства зависит только от разности (s_i – s_j)mod n, которую назовем относительным сдвигом Y^↓_i и Y^↓_j. Заметим также, что

 

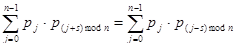, (7)

 

поэтому Y^↓_i и Y^↓_j с относительными сдвигами s и п-s имеют одинаковые взаимные индексы совпадения. Приведем таблицу значений сумм (7) для английского языка:

 

Таблица 8. Взаимный индекс совпадения при сдвиге s

Сдвиг s	0	1	2	3	4	5	6
	0,066	0,039	0,032	0,034	0,044	0,033	0,036
Сдвиг s	7	8	9	10	11	12	13
	0,039	0,034	0,034	0,038	0,045	0,039	0,043

 

Обратим внимание на то, что ненулевые "сдвиги" дают взаимные индексы совпадения, изменяющиеся в пределах от 0,032 до 0,045, в то время как при нулевом сдвиге индекс MI_c(x,y) близок к 0,066. Это наблюдение позволяет определить величины относительных сдвигов s_i – s_j столбцов Y^↓_i и Y^↓_j. Для этого заметим, что при некотором значении s(i,j) 0, n-1столбец Y^s(i,j)↓_j, полученный из Y^↓_j прибавлением к каждому его элементу числа S(i,j) (по модулю n), имеет нулевой относительный сдвиг с Y^↓_j.

Пусть Y^0↓_j, Y^1↓_j,…, Y^n-1↓_j – результаты зашифрования Y^↓_j каждой из простых замен (5). Несложно вычислить взаимные индексы

 

 

(всего, таким образом, имеется С²_µn значений). Для этого воспользуемся формулой, полученной из (6):

 

 

Если s равно s_i – s_j - (относительному сдвигу Y^↓_i и Y^↓_j), то взаимный индекс впадения должен быть (для английского языка) близок к 0,066, так как относительный сдвиг Y^↓_i и Y^↓_j равен нулю. Если же s не равно s_i – s_j то взаимный индекс совпадения должен колебаться в пределах 0,032 - 0,045.

Используя изложенный метод, мы сможем связать системой уравнений относительные сдвиги различных пар столбцов Y^↓_i и Y^↓_j. В результате останется 26 (для английского языка) вариантов для ключевого слова, из которых можно выбрать наиболее предпочтительный вариант (если ключевое слово является осмысленным).

Следует отметить, что предложенный метод будет эффективным для не слишком больших значений µ. Это объясняется тем, что для хороших сближений индексов совпадения требуются тексты достаточно большой длины.

Пример криптоанализа текста:

Задан некоторый текст зашифрованный шифром Виженера, требуется определить ключевое слово и прочитать открытый текст.

 

Шифрованный текст:

 

влцдутжбюцхъяррмшбрхцэооэцг брь цмйфктъъюьмшэсяцпунуящэйтаьэдкци брь цгбрпачкъуцпъбьсэгкцъгуущарцёэвърюуоюэкааэбрняфукабъарпяъафкъиьжяффнйояфывбнэнфуюг брь сшьжэтбэёчюъюръегофкбьчябашвёэуъъюаднчжчужцёэвлрнчулбюпцуруньъшсэюъзкцхъяррнрювяспэмасчкпэужьжыатуфуярюравртубурьпэщлафоуфбюацмнубсюкйтаьэдйюнооэгюожбгкбрънцэпотчмёодзцвбцшщвщепчдчдръюьскасэгъппэгюкдойрсрэвоопчщшоказръббнэугнялёкьсрбёуыэбдэулбюасшоуэтъшкрсдугэфлбубуъчнчтртпэгюкиугюэмэгюккъъпэгяапуфуэзьрадзьжчюрмфцхраююанчёчюъыхьъцомэфъцпоирькнщпэтэузуябащущбаыэйчдфрпэцъьрьцъцпоилуфэдцойэдятррачкубуфнйтаьэдкцкрннцюабугюуубурьпйюэъжтгюркующоъуфъэгясуоичщщчдцсфырэдщэъуяфшёчцюйрщвяхвмкршрпгюопэуцчйтаьэдкци брь цыяжтюрбуэтэбдуящэубъибрювъежагибрбагбрымпуноцшяжцечкфодщоъчжшйуъцхчщвуэбдлдъэгясуахзцэбдэулькнъщбжяцэьрёдъьвювлрнуяфуоухфекьгцчччгэъжтанопчынажпачкъуъмэнкйрэфщэъьбудэндадъярьеюэлэтчоубъцэфэвлнёэгфдсэвэёкбсчоукгаутэыпуббцчкпэгючсаъбэнэфъркацхёваетуфяепьрювържадфёжбьфутощоявьъгупчршуитеачйчирамчюфчоуяюонкяжыкгсцбрясшчйотъъжрсщчл

 

Для определения числа букв в данном ключевом слове применяется так называемый тест Казиски. Тест основан на простом наблюдении о том, что два одинаковых отрезка открытого текста, отстоящих друг от друга на расстоянии, кратном µ (количество букв в слове), будут одинаково зашифрованы. В силу этого в шифр-тексте ищутся повторения длины, не меньшей трех, и расстояния между ними. Необходимо обратить внимание на то, что случайно такие одинаковые отрезки могут появиться в тексте с достаточно малой вероятностью

В данном тексте обнаружено четырехкратное повторение буквосочетания «брь». Выясним расстояние между ними и найдем наибольший общий делитель этих расстояний.

В результате получаем: 35, 85, 510

НОД = 5;

Следовательно, с определенной долей вероятности можно заключить, что длина кодового слова равна 5.

Для подтверждения гипотезы воспользуемся математической статистикой для определения длины ключевого слова. Для этого запишем шифр-текст в таблицу с 5 столбцами, предполагая, что длина ключевого слова равна 5.

Вычислим взаимные индексы совпадения I_C(x) букв в каждом из столбцов таблицы, для достоверного установления длины ключевого слова. Для этого посчитаем частоту повторения букв в каждом столбце. Таблица состоит из 5 столбцов, так как на предыдущем этапе нами было установлено, что ключевое слово по НОД может состоять из 5 букв.

 

Y1	Y2	Y3	Y4	Y5
в	л	ц	д	у
Т	ж	б	ю	ц
Х	ъ	я	р	р
М	ш	б	р	х
Ц	э	о	о	э
Ц	г	б	р	ь
Ц	м	й	ф	к
Т	ъ	ъ	ю	ь
М	ш	э	с	я
Ц	п	у	н	у
Я	щ	э	й	т
А	ь	э	д	к
Ц	и	б	р	ь
Ц	г	б	р	п
А	ч	к	ъ	у
Ц	п	ъ	б	ь
С	э	г	к	ц
Ъ	г	у	у	щ
А	р	ц	ё	э
В	ъ	р	ю	у
О	ю	э	к	а
А	э	б	р	н
Я	ф	у	к	а
Б	ъ	а	р	п
Я	ъ	а	ф	к
Ъ	и	ь	ж	я
Ф	ф	н	й	о
Я	ф	ы	в	б
Н	э	н	ф	у
Ю	г	б	р	ь
С	ш	ь	ж	э
Т	б	э	ё	ч
Ю	ъ	ю	р	ъ
Е	г	о	ф	к
Б	ь	ч	я	б
А	ш	в	ё	э
У	ъ	ъ	ю	а
Д	н	ч	ж	ч
У	ж	ц	ё	э
В	л	р	н	ч
У	л	б	ю	п
Ц	у	р	у	н
Ь	ъ	ш	с	э
Ю	ъ	з	к	ц
Х	ъ	я	р	р
Н	р	ю	в	я
С	п	э	м	а
С	ч	к	п	э
У	ж	ь	ж	ы
А	т	у	ф	у
Я	р	ю	р	а
В	р	т	у	б
У	р	ь	п	э
Щ	л	а	ф	о
У	ф	б	ю	а
Ц	м	н	у	б
С	ю	к	й	т
А	ь	э	д	й
Ю	н	о	о	э
Г	ю	о	ж	б
Г	к	б	р	ъ
Н	ц	э	п	о
Т	ч	м	ё	о
Д	з	ц	в	б
Ц	ш	щ	в	щ
Е	п	ч	д	ч
Д	р	ъ	ю	ь
С	к	а	с	э
Г	ъ	п	п	э
Г	ю	к	д	о
Й	р	с	р	э
В	о	о	п	ч
Щ	ш	о	к	а
З	р	ъ	б	б
Н	э	у	г	н
Я	л	ё	к	ь
С	р	б	ё	у
Ы	э	б	д	э
У	л	б	ю	а
С	ш	о	у	э
Т	ъ	ш	к	р
С	д	у	г	э
Ф	л	б	у	б
У	ъ	ч	н	ч
Т	р	т	п	э
Г	ю	к	и	у
Г	ю	э	м	э
Г	ю	к	к	ъ
Ъ	п	э	г	я
А	п	у	ф	у
Э	з	ь	р	а
Д	з	ь	ж	ч
Ю	р	м	ф	ц
Х	р	а	ю	ю
А	н	ч	ё	ч
Ю	ъ	ы	х	ь
Ъ	ц	о	м	э
Ф	ъ	ц	п	о
И	р	ь	к	н
Щ	п	э	т	э
У	з	у	я	б
А	щ	у	щ	б
А	ы	э	й	ч
Д	ф	р	п	э
Ц	ъ	ь	р	ь
Ц	ъ	ц	п	о
И	л	у	ф	э
Д	ц	о	й	э
Д	я	т	р	р
А	ч	к	у	б
У	ф	н	й	т
А	ь	э	д	к
Ц	к	р	н	н
Ц	ю	а	б	у
Г	ю	у	у	б
У	р	ь	п	й
Ю	э	ъ	ж	т
Г	ю	р	к	у
Ю	щ	о	ъ	у
Ф	ъ	э	г	я
С	у	о	и	ч
Щ	щ	ч	д	ц
С	ф	ы	р	э
Д	щ	э	ъ	у
Я	ф	ш	ё	ч
Ц	ю	й	р	щ
В	я	х	в	м
К	р	ш	р	п
Г	ю	о	п	э
У	ц	ч	й	т
А	ь	э	д	к
Ц	и	б	р	ь
Ц	ы	я	ж	т
Ю	р	б	у	э
Т	э	б	д	у
Я	щ	э	у	б
Ъ	и	б	р	ю
В	ъ	е	ж	а
Г	и	б	р	б
А	г	б	р	ы
М	п	у	н	о
Ц	ш	я	ж	ц
Е	ч	к	ф	о
Д	щ	о	ъ	ч
Ж	ш	й	у	ъ
Ц	х	ч	щ	в
У	э	б	д	л
Д	ъ	э	г	я
С	у	а	х	з
Ц	э	б	д	э
У	л	ь	к	н
Ъ	щ	б	ж	я
Ц	э	ь	р	ё
Д	ъ	ь	в	ю
В	л	р	н	у
Я	ф	у	о	у
Х	ф	е	к	ь
Г	ц	ч	ч	ч
Г	э	ъ	ж	т
А	н	о	п	ч
Ы	н	а	ж	п
А	ч	к	ъ	у
Ъ	м	э	н	к
Й	р	э	ф	щ
Э	ъ	ь	б	у
Д	э	н	д	а
Д	ъ	я	р	ь
Е	ю	э	л	э
Т	ч	о	у	б
Ъ	ц	э	ф	э
В	л	н	ё	э
Г	ф	д	с	э
В	э	ё	к	б
С	ч	о	у	к
Г	а	у	т	э
Ы	п	у	б	б
Ц	ч	к	п	э
Г	ю	ч	с	а
Ъ	б	э	н	э
Ф	ъ	р	к	а
Ц	х	ё	в	а
Е	т	у	ф	я
Е	п	ь	р	ю
В	ъ	р	ж	а
Д	ф	ё	ж	б
Ь	ф	у	т	о
Щ	о	я	в	ь
Ъ	г	у	п	ч
Р	ш	у	и	т
Е	а	ч	й	ч
И	р	а	м	ч
Ю	ф	ч	о	у
Я	ю	о	н	к
Я	ж	ы	к	г
С	ц	б	р	я
С	ш	ч	й	о
Т	ъ	ъ	ж	р
С	щ	ч	л

 

Частота повторения букв в столбцах:

1 столбец (общее количество букв m=198)

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	17	2	10	16	14	7	0	1	1	3	2	1	0
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	3	4	1	0	1	16	9	14	5	5	23	0	0
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	5	10	3	2	2	10	11

 

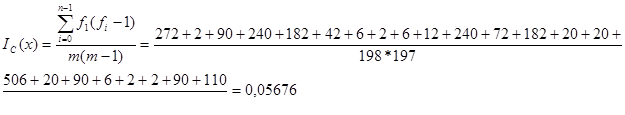
2 столбец (общее количество букв m=198)

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	2	2	0	7	1	0	0	4	4	5	0	3	11
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	3	5	2	10	18	0	2	3	14	2	7	9	11
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	9	26	2	5	14	15	2

 

 

3 столбец (общее количество букв m=198)

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	9	24	1	1	1	2	4	0	1	0	3	10	0
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	2	6	17	1	9	1	3	19	0	1	6	14	4
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	1	8	4	14	23	3	6

 

4 столбец (общее количество букв m=198)

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	0	5	8	5	13	0	9	16	0	3	9	15	2
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	4	9	4	14	27	5	3	13	13	2	0	1	0
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	2	5	0	0	0	9	2

 

5 столбец (общее количество букв m=197)

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	15	18	1	1	0	0	1	0	1	0	2	9	1
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	1	6	11	5	5	0	8	19	0	1	6	17	0
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	4	4	2	13	33	4	9

 

 

По полученным индексам совпадения можно сказать, что длина ключевого слова выбрана верно и равна 5.

После того как мы нашли длину ключевого слова произведем поиск его истинного значения. Для его нахождения можно использовать так называемый взаимный индекс совпадения

 

., где

- частота буквы i в столбцах  соответственно;

m, m` - число букв в столбцах  соответственно;

Так как каждый из столбцов таблицы является результатом зашифрования фрагмента открытого текста простой заменой, определяемой подстановкой, то попытаемся оценить взаимные индексы совпадения.

Взаимный индекс совпадения значения ключевого слова для русского языка должен находиться в приделах 0.053 – 0,07. И для его вычисления предварительно необходимо определить относительный сдвиг всех столбцов относительно первого.

 

Сдвиг 2-го столбца на 6 позиций

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	26	2	5	14	15	2	2	2	0	7	1	0	0
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	4	4	5	0	3	11	3	5	2	10	18	0	2
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	3	14	2	7	9	11	9

 

MI_c(Y1,Y2⁶)= 0.05494

 

Сдвиг 3-го столбца на 3 позиции

 

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	23	3	6	9	24	1	1	1	2	4	0	1	0
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	3	10	0	2	6	17	1	9	1	3	19	0	1
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	6	14	4	1	8	4	14

 

MI_c(Y1,Y3³)= 0.5798

 

Сдвиг 4-го столбца на 16 позиций

 

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	27	5	3	13	13	2	0	1	0	2	5	0	0
Обозначение	м	н	о	п	р	с	т	у	ф	х	ц	ч	ш
Количество	0	9	2	0	5	8	5	13	0	9	16	0	3
Обозначение	щ	ъ	ы	ь	э	ю	я
Количество	9	15	2	4	9	4	14

 

MI_c(Y1,Y4¹⁶)= 0.06068

 

Сдвиг 5-го столбца на 3 позиции

Обозначение	а	б	в	г	д	е	ё	ж	з	и	й	к	л
Количество	33	4	9	15	18	1	1	0	0	1	0	1	0
<

Предыдущая12345678Следующая

Поделиться:

Воспользуйтесь поиском по сайту: