Законы затухания люминесценции

1. Внутрицентровой люминесценции.

Легко показать. что закон затухания внутрицентровой люминесценции, имеющей мономолекулярный характер, представляет собой экспоненту.

Пусть N0- число возбужденных центров свечения в момент прекращения возбуждения, N - число возбужденных центров свечения в некоторый момент времени t, α - вероятность излучательного перехода возбужденного центра свечения в основное состояние.

Если в кристалле отсутствует тушение люминесценции, вероятность безизлучательных переходы полагают равной нулю. Тогда уменьшение числа возбужденных центров свечения -dN за малое время dt равно αNdt,т.е.

 

-dN=αNdt; N=N₀e^-αt

 

Интенсивность люминесценции пропорциональна уменьшению числа возбужденных центров свечения в единицу времени:

 

I ≅ -dN/dt = αN = αN₀e^-αt; I = I₀e^-αt= I₀e-t/τ                    (1)

 

где I₀ - интенсивность люминесценции в момент прекращения возбуждения, τ- время, за которое начальная интенсивность уменьшается в e раз, т.е. τ-длительность люминесценции. Очевидно, что τ как раз равно среднему времени жизни центра свечения в возбужденном состоянии.

2. Рекомбинационной люминесценции

Вначале найдем закон затухания люминесценции в идеализированном случае когда в кристаллофосфоре есть только центры свечения и полностью отсутствуют какие-либо центры захвата. Тогда число ионизированных центров свечения N и электронов в зоне проводимости n в точности равно между собой в любой момент времени.

Если β - вероятность рекомбинации электрона с центром свечения, то уменьшение количества ионизированных центров свечения за время dt можно выразить следующим образом:

 

-dN = βNndt = βN²dt.

 

Интегрируя, получим:

 

1/N = βt+ const.

 

Если отсчёт времени вести от момента снятия возбуждения и через N₀ обозначить число ионизированных центров свечения в момент t, то 

 

const = 1/N₀ и 1/N = βt + 1/N₀; N=N₀/(1+βN₀t)

Если пренебречь вероятностью безизлучательных переходов возбужденных центров свечения в основное состояние (как указывалось выше, после рекомбинации электрона с ионизированным центром свечения, последний находится в возбужденном состоянии), то интенсивность люминесценции можно считать пропорциональной -dN/dt. Поэтому

 

I ~ dN/dt = βN²; I = βN₀²/(1+βN₀t)²

 

при t = 0 I = I₀ = βN₀²

 

I = I₀/(1=(βI₀)^1/2t)²; I = I₀/(1+αt)²                             (2)

 

Таким образом, для кристаллофосфора, не имеющего центров захвата, закон затухания представляет собой гиперболу второго порядка. Опыт показывает, что в некоторых редких случаях затухание люминесценции кристаллофосфоров действительно идет по гиперболе второго порядка. Однако чаще всего, как было указано Беккерелем в 1868 г, экспериментально наблюдаемые законы затухания представляют собой гиперболу с показателем степени меньшим двух:

 

              I = I₀/(1+at)^α: где 1≤ α≥2                            (3)

 

Несовпадение выводов приведенного выше теоретического рассмотрения с результатами эксперимента вполне понятно, т.к. вывод закона затухания (2) был проведен для идеализированного положения вещей. Мы рассмотрели фосфор только с одними центрами свечения, без центров захвата. В реальном кристаллофосфоре наряду с центрами свечения имеется большое число различных центров захвата, Кроме того, бывают кристаллофосфоры, содержащие центры свечения двух, трех и т.д. видов. Задача теоретического отыскания закона затухания для реального кристаллофосфора очень сложна. Поэтому мы ограничимся рассмотрением только гипотетического кристаллофосфора следующие обозначения:

N - концентрация ионизированных центров свечения, n_э - концентрация электронов, локализованных на центрах захвата (число заполненных ловушек), ν - концентрация ловушек, n - концентрация электронов в зоне проводимости,σ_з - эффективное сечение захвата электрона ловушкой, σ_р - эффективное сечение захвата электрона центром свечения, ω или p - вероятность теплового освобождения электрона из ловушки глубины Е.

Постоянные σ_р и σ_з имеют размерность см². В первом приближении σ_р и σ_з можно рассматривать как площадь, ограниченную кругом радиуса, равного максимальному расстоянию, на котором может произойти рекомбинация или захват электрона.

P =σ_рU - вероятность рекомбинации электрона с центром свечения, σ_зU -  вероятность захвата электрона ловушкой.

Для любого момента времени в процессе затухания люминесценции кристалофосфора выполняются следующие соотношения:

                        dn/dt = ω n_з - βnN - σ_зnU(ν - n_з)                         (4)

 

                                    dN/dt = -βnN                                         (5)

 

                          dn_з/dt = -ω n_з + σ_зnU(ν - n_з)                               (6)

 

                                      N = n + n_з                                              (7)

 

Записанная система не решается в элементарных функциях.

Введем некоторые приближения, основанные на физических соображениях. Длительность послесвечения определяется большим из двух характеристических времен - средним временем жизни электрона в ловушке (τ = 1/ω) и средним временем жизни в зоне проводимости t₀. Если τ ~ t₀, или τ < t₀, то длительность послесвечения будет составлять малые доли секунды. Кристаллофосфор с длительным послесвечением имеет τ >> t₀, т.е. время жизни электрона в ловушке много больше его времени жизни в зоне проводимости. При выполнении условия τ >> t₀ можно ожидать малую квазистационарную концентрацию свободных электронов. Приближение, в котором dn/dt полагают равным нулю, т.е. число электронов в зоне проводимости считают некоторой малой постоянной величиной, называют квазистационарным.

В квазистационарном приближении уравнения (4) - (7) принимают следующий вид:

βnN = ω n_з  - σ_зnU(ν - n_з)                               (4’)

 

dN/dt = -βnN                                        (5’)

 

dn_з/dt = dN/dt = -ω n_з + _зnU(ν - n_з)                      (6’)

 

N =n_з                                                 (7’)

 

Из (4’):

 

n = ωn_з/(βN - σ_зU(ν - n_з)

 

Используя (7’) можно записать

 

n = ωN/(βN - σ_зU(ν - n_з)

 

Подставив полученное выражение в (5), найдем:

т.к. β=σ_pU, полученное соотношение можно переписать, введя отношение эффективных сечений захвата и рекомбинации

                                        

(8)

 

Рассмотрим выражение в двух предельных случаях:

а) σ∼σ p, т.е. γ=1. Соотношение (8) примет вид:

                                                  

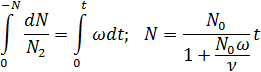
Интегрируя, получим:

 

 

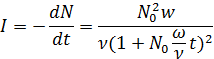
или

                                                   I=I₀/(1+αt)²

т.е., в случае равенства эффективных сечений захвата и рекомбинации закон затухания представляет гиперболу второго порядка

б) Эффективное сечение захвата гораздо меньше эффективного сечения рекомбинации электрона с центром свечения, т.е γ=0. Соотношение (8) примет вид

                                           -dN/dt=ωN; N=N₀e^-ωt

т.е. затухание рекомбинационной люминесценции в данном случае идет по экспоненте. Для произвольных значений γ, интегрируя соотношение (8), можно найти зависимость N от t лишь в неявном виде:

 

(9)

 

Соотношения (8) и (9) представляют собой запись закона затухания люминесценции кристаллофосфора в параметрическом виде. В эти соотношения входят параметры ω, γ, ν, N₀, определяемые условиями опыта- температурой и временем возбуждения.

Адирович [13] предложил сократить число параметров в уравнениях (8) и (9) проведением подходящей замены переменных:

µ=N / ν - безразмерная характеристика светосуммы;

β=(τ / ν)I — безразмерная интенсивность;

V=t/τ - время в единицах τ где τ - среднее время жизни электрона в ловушках;

Z=N₀ / ν - характеристика степени возбуждения фосфора;

L=N/N₀ - величина, характеризующая светосуммы в текущий момент и начальный момент времени.

Используя введенные обозначения, соотношения (8) и (9) можно переписать в следующем виде:

 

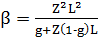 (8’)

 

 (9’)

 

Закон затухания, записанный в виде соотношений (8’) и (9’) включает два параметра Z и γ и носит название закона затухания в безразмерном виде. Параметры ω=1/τ и ν определяют масштаб единиц времени и интенсивности. Для кристаллофосфоров с одинаковыми γ, но различными ν и τ теоретические кривые в безразмерных осях V и β совпадают. Это облегчает анализ кривых затухания. Адирович провел численные расчеты затухания для кристаллофосфоров с различными γ в условиях “насыщения”, т.е. при таких условиях возбуждения, когда все ловушки оказываются заполненными

электронами. В условиях насыщения

 

Z=N₀/ν=1 и µ=N/ν=N/N₀=L

 

Соотношения (8’) и (9’) принимают вид:

                                                     

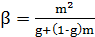 (8”)

                                              

 (9”)

Анализ кривых, построенных по расчетным данным, показал, что на основном

центральном участке они могут быть аппроксимированы дробной гиперболой:

 

β=C / (1+V)^α

 

т.к. β=I_τ/ν, а V=t/τ, можно записать

 

                                           I=I₀/(1+αt)^α       (3)

 

Этот участок кривой затухания был назван беккерелевским.

Область остаточных светосумм характеризуется малой интенсивностью и медленным высвечиванием. Для этой области µ=N/ν<<1 и поэтому β∼µ²/γ а V= γ / µ. Следовательно, β ≈ γ / V². Т.к. V>>1 на дальних стадиях затухания, то к V можно прибавить 1, не внося большой ошибки. Тогда

β∼1/(1+V)²

т.е. затухание люминесценции в конце высвечивания идет по гиперболе второго порядка. Этот вывод согласуется с экспериментом. Теория Адировича впервые объяснила экспериментальную формулу Беккереля для закона затухания кристаллофосфора, а также квадратичную зависимость интенсивности люминесценции от времени на дальних стадиях затухания для слабо возбужденных фосфоров. В дальнейшем в работах Антонова- Романовского [14], Фока [15] и других были предприняты попытки теоретического отыскания закона затухания люминесценции кристаллофосфоров с двумя различными сортами центров захвата, учетом эффекта тушения люминесценции и т.д.

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: