 |
Зависимость между координатами точки местности и снимка
|
|
|
|
Точка местности М и её изображение на снимке т находятся на одном проектирующем луче (рис.31). Положение точек S и М в системе координат местности X Y Z определяется векторами соответственно  , а положение точек т и М в системе координат S X' Y' Z' – векторами
, а положение точек т и М в системе координат S X' Y' Z' – векторами  .
.
Векторы  коллинеарны, поэтому
коллинеарны, поэтому
 , ,
| (24) |
 |
где λ – скаляр, а
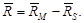
Спроектируем векторы  на координатные оси X, Y, Z, тогда:
на координатные оси X, Y, Z, тогда:

| (25) |
Из третьего равенства (25) найдем λ и подставим его выражение в первое и второе. Тогда:

| (26) |
Так как

то
 , ,
| (27) |
Или, с учётом равенства (15)

| ((28) |
Итак, если элементы ориентирования снимка даны, то два уравнения (27) имеют три неизвестных. Отсюда следует, что пространственные координаты точки местности по одиночному снимку не определить. Можно получить лишь ее плановое положение. Но надо знать высоту фотографирования H = - (Z – ZS).
В фотограмметрии часто используются обратные зависимости (между координатами точки снимка и координатами соответствующей точки местности). Для их получения, спроектируем векторы  равенства (24) на координатные оси системы координат S x y z (рис. 31), в результате получим:
равенства (24) на координатные оси системы координат S x y z (рис. 31), в результате получим:

| (29) |
Решим третье уравнение относительно λ и подставим его значение в первое и второе уравнения. Тогда:

| (30) |
Матрицы-столбцы равенств (29) можно представить в виде:
 ; ;
| ((31) |

| ((32) |
Подставив выражения проекций векторов r и R из (31) и (32) в (30), будем иметь:

| (33) |
Формулы (28) и (33) справедливы при любых значениях элементов ориентирования снимка.
Пусть x 0 = y 0 = 0, X S = Y S = 0, Z S – Z = H, тогда при условии расположения осей как на рис. 24 (снимок можно считать горизонтальным) формулы (28) и (33) будут выглядеть следующим образом:
|
|
|

| (34) |
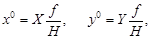
| (35) |
где x 0, y 0 – координаты точки горизонтального снимка.
Предположим теперь, что снимок наклонный, но при этом  Матрица преобразования координат A будет иметь вид:
Матрица преобразования координат A будет иметь вид:

| (36) |
И при указанных выше условиях (x 0 = y 0 = 0, X S = Y S = 0, Z S – Z = H), получим:
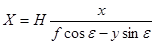 и
и  (37)
(37)
Уравнения (37) записаны для случая, когда начало координат на местности совмещено с точкой S или N, а на снимке - с главной точкой о. Если же начала координат перенести соответственно в точки C и c, то соотношения станут еще более простыми:
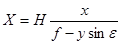 , ,
| 
| (38) |
При условии, что за начало координат на местности принята точка N, а на снимке – соответствующая ей точка надира n, справедливы следующие соотношения;
 , , 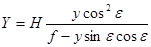
| (39) |
Уравнения (38) и (39) легко получить из соотношения 37 и переносом систем координат на снимке и в пространстве.
ЗАВИСИМОСТЬ МЕЖДУ КООРДИНАТАМИ ТОЧКИ ГОРИЗОНТАЛЬНОГО И НАКЛОННОГО СНИМКОВ.
В фотограмметрии часто применяются зависимости между координатами точек горизонтального и наклонного снимков. Их легко получить из уравнений (28) и (34), с учетом того, что Z S – Z = H и координаты главной точки равны нулю. Левые части этих уравнений выражают одни и те же величины – координаты X и Y точки местности. Поэтому справедливо:

Откуда

| (40) |
Таким образом, если даны его угловые элементы внешнего ориентирования, то по формулам (40) можно перейти от координат точек на наклонном снимке, к координатам соответствующих точек на горизонтальном снимке. Этот процесс называется трансформированием координат. Они справедливы при любых значениях угловых элементов внешнего ориентирования снимка.
Подставив в уравнения (40) выражения направляющих косинусов из (21), после преобразований с точностью до членов второго порядка малости получим:

| (41) |
Приведенные формулы проще, но они перестали быть строгими.
|
|
|
Строгие и простые соотношения можно написать, если начало координат на снимке и на местности совместить с точкой нулевых искажений с, тогда с учетом уравнений (34) и(38) получим:
 , , 
| (42) |
МАСШТАБ СНИМКА.
Масштабом снимка 1/ m в данной точке по данному направлению называется отношение бесконечно малого отрезка dl на снимке к соответствующему отрезку dL на местности. То есть:
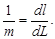
| (43) |
 |
Пусть местность равнинная, а начала координат в пространстве и на снимке расположены соответственно в точках S и o,(рис. 32).
Обозначив проекции отрезков dl и dL на соответствующие координатные оси через dx, dy и dX, dY, с учетом данного определения масштаба и рис. 32 напишем:
 , ,
| (44) |
где φ – угол между осью x снимка и заданным направлением отрезка dl.
При указанном выборе систем координат, и при условии, что оси ординат расположены в плоскости главного вертикала, справедливы уравнения (37) зависимости между координатами точек местности и снимка. Продифференцируем их по переменным x и y, в результате получим:
 .
.
Введём обозначение:
 .
.
и учтем, что dy=dxtgj, тогда

| (45) |
Подставив выражения dX и dY из соотношений (45) в формулу (44), будем иметь:
 . .
| (46) |
Полученное равенство показывает, что масштаб снимка зависит от фокусного расстояния АФА, высоты фотографирования, угла наклона снимка, положения точки на снимке (координат x и y), в которой взят элемент dl и от направления φ этого элемента относительно линии главного вертикала  .
.
Определим значение масштаба 1/ m для частных случаев.
1. Масштаб горизонтального снимка (ε = 0). Подставив это значение в формулу (46), с учетом принятых обозначений k и p получим:
 ,
,
т. е. масштаб горизонтального снимка плоской местности во всех точках постоянный.
2. Масштаб наклонного снимка по направлению главной вертикали (x = 0, φ = 90°):
 . .
| (47) |
На основании уравнения (47) запишем значение масштаба 1/ m в характерных точках, лежащих на линии главного вертикала:
В главной точке снимка o (y = 0)
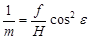 ;
;
В точке нулевых искажений с  , поэтому:
, поэтому:
 ;
;
В точке надира n 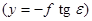 , после подстановки получаем:
, после подстановки получаем:
 ;
;
В главной точке схода 
 .
.
Таким образом, масштаб в точке нулевых искажений равен, в главной точке мельче, а в точке надира крупнее масштаба горизонтального снимка. Масштаб в точке нулевых искажений называется главным масштабом снимка.
|
|
|
3. Масштаб наклонного снимка по направлению горизонтали (φ = 0°)

| (48) |
Поскольку в уравнении абсцисса точки отсутствует, то вдоль горизонтали, если местность равнинная, мосштаб величина постоянная.
Запишем выражения 1/ m для горизонталей, проходящих через характерные точки снимка:
По линии действительного горизонта 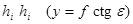 , поэтому:
, поэтому:
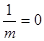 ;
;
Вдоль главной горизонтали  , после подстановки имеем:
, после подстановки имеем:
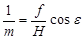 ;
;
На линии неискажённого масштаба  , значит
, значит
 ;
;
По горизонтали hnhn, проходящей через точку надира  , и:
, и:
 .
.
Выполненный анализ показал, что масштаб снимка в точке c по любому направлению равен масштабу горизонтального снимка.
|
|
|


