Определение элементов внешнего ориентирования снимка

Для решения ряда фотограмметрических задач необходимо знать элементы ориентирования снимка.

Его элементы внешнего ориентирования могут быть получены либо с помощью специальных приборов в процессе аэрофотосъёмки либо в камеральных условиях по геодезическим и фотокоординатам опорных точек. Второй вариант назвали обратной пространственной фотограмметрической засечкой. Математической основой ее решения являются прямые или обратные уравнения коллинеарности.

Рассмотрим один из возможных способов математического решения засечки, основанный на применении уравнений (33).

Пусть на снимке изобразились точки местности, геодезические координаты которых известны (такие точки называют опознаками), и координаты x, y этих точек определены по данным измерений снимка. Примем, что элементы внутреннего ориентирования снимка даны. Тогда неизвестными величинами в формулах (33) окажутся координаты X_S,, Y_S,, Z_S центра проекции снимка и три угла 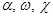. Указанные уравнения нелинейны по отношению к неизвестным, поэтому последние определяются способом приближений. То есть, вначале из каких-либо соображений принимают приближенные значения неизвестных, а затем определяют поправки к ним, используя технику уравнивания параметрическим способом. Таким образом, задачу решают следующим образом:

1. Определяют приближенные значения элементов внешнего ориентирования снимка. Например, угловые величины принимают равными нулю, а координаты центра проекции определяют по данным бортовых измерений или каким-либо другим способом.

2. Выполняют измерение с целью определения координат x и y опознаков на снимках.

3. Приближенные значения элементов внешнего ориентирования, а также элементы внутреннего ориентирования и заданные координаты опознаков подставляют в уравнения (33) и вычисляют координаты x¢ и y^¢ изображений опознаков на снимке. В силу погрешностей измерений, неточности приближенных величин, принятых в качестве неизвестных, и других причин вычисленные координаты не будут равны измеренным.

4. Составляют уравнения поправок, принимая разности l между измеренными и вычисленными координатами точек на снимке в качестве их свободных членов. Указанные уравнения будут иметь вид:

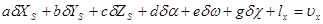
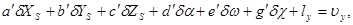
(56)

где 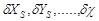- поправки в приближённые значения элементов внешнего ориентирования снимка; l_x=x - x¢; l_y=y - y^¢; , – поправки в измеренные координаты x, y. Численные значения коэффициентов a, b, …, g' уравнений (56) вычисляются как частные производные функций x, y (уравнения 33) по соответствующим переменным. Например:

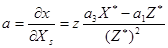и т.д.

Система уравнений (56) содержит шесть неизвестных. Один опознак позволяет составить два уравнения, поэтому для решения задачи их должно быть не менее трех.

5. При избыточном количестве опознаков система линейных уравнений решается при условии

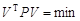
где Р – матрица весов измеренных координат точек снимка.

То есть составляют и решают нормальные уравнения. Для системы (56) они имеют вид:

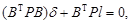
(57)

где В – матрица коэффициентов a, b, …, g' для опорных точек снимка; δ – вектор поправок 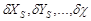; l – вектор свободных членов уравнений (56).

Решая уравнения (57), определяют вектор поправок

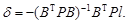
(58)

6. Вводят поправки δ к приближённым значениям элементов внешнего ориентирования, получают уточнённые значения неизвестных. Поскольку исходная система (35) нелинейная, а приближённые значения могут существенно отличаться от искомых величин, вычисления повторяют, начиная с пункта 3, и продолжают их до тех пор, пока разность векторов δ двух последних приближений не станет меньше установленного допуска. Такой путь решения называют методом итераций.

7. Выполняют оценку точности решения задачи. Для этого в последнем приближении вычисляют весовые коэффициенты Q и поправки V. Средние квадратические ошибки элементов вычисляют по формуле:

,

(59)

где i = 1, 2, 3,…,6 – номер поправки δ в уравнениях (56).

Ошибка единицы веса находят из соотношения

,

(60)

где п – число опорных точек.

Иногда, например, при калибровке камер, возникает задача определения и элементов внутреннего ориентирования снимка. В этом случае необходимо дополнить матрицу δ поправками 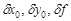, а матрицу В – коэффициентами h, m, n, h', m', n' при определяемых поправках. Поскольку количество неизвестных увеличивается до 9, число опознаков необходимых для решения задачи, должно быть не менее 5, а ошибка единицы веса должна определяться по формуле:

.

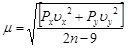(61)

Следует иметь в виду, что при аэрофотосъёмке равнинной местности включение дополнительных неизвестных в систему уравнений поправок приводит к ухудшению обусловленности матрицы системы нормальных уравнений. Это приводит к снижению точности определения искомых величин.

Теория пары снимков.