Основные положения нестрогой математики

Нестрогой математикой, или математикой здравого смысла (называемой еще теорией лингвистических переменных) будем называть совокупность приемов построения и использования моделей больших систем, основывающихся на неформальных суждениях и умозаключениях человека, формируемых им исходя из жизненного опыта и здравого смысла. Интерес к такой математике проявляется в последние годы в связи с все возрастающей актуальностью задач анализа и синтеза организационных систем, а также управления процессами их функционирования. Как известно, многие системы организационного типа характеризуются высоким уровнем неопределенности, в силу чего не удается построить адекватные им модели с помощью средств традиционных методов моделирования. Необходим аппарат с таким диапазоном представления и оперирования, который был бы адекватен уровню неопределенности моделируемых систем. Характерными примерами таких систем являются системы, основные цели функционирования которых определяются потребностями людей. Нестрогая математика и представляется как основа методологии моделирования таких систем. К сожалению, в имеющихся публикациях отсутствует системное изложение данной методологии.

Поскольку основной объект нашего изучения - системы защиты информации - относится к системам с весьма высоким уровнем неопределенности (нарушение статуса защищенности информации, как правило, обусловливается целями и действиями людей), то представляется целесообразным включить методологию нестрогой математики в арсенал средств, предназначаемых для использования при решении проблем защиты. Этим и обусловлено выделение данного вопроса в самостоятельный раздел методологических основ защиты информации.

Исходным базисом нестрогой математики служит совокупность трех посылок:

1)в качестве меры характеристик изучаемых систем вместо числовых переменных или в дополнение к ним используются лингвистические переменные. Если, например, нас интересует такая характеристика, как вероятность доступа нарушителя к защищаемой информации, то в лингвистическом измерении значениями этой характеристики могут быть: «крайне незначительная», «существенная», «достаточно высокая», «весьма высокая» и т.п.;

2)простые отношения между переменными в лингвистическом измерении описываются с помощью нечетких высказываний, которые имеют следующую структуру: «из А следует В», где А и В - переменные в лингвистическом измерении. Примером такого отношения может быть: «Если в системе охранной сигнализации вероятность отказов датчиков значительная, то для предупреждения проникновения на контролируемую территорию посторонних лиц интенсивность организационного контроля над этой территорией должна быть повышенной». Переменными здесь являются «вероятность отказов датчиков» и «интенсивность организационного контроля», а лингвистическими значениями - «значительная» и «повышенная» соответственно;

3)сложные отношения между переменными в лингвистическом измерении описываются нечеткими алгоритмами. В качестве примера рассмотрим нечеткий алгоритм сложного отношения между переменными: «надежность компонентов системы защиты информации» и «интенсивность контроля храни лища носителей защищаемой информации».

Совершенно очевидно, что интенсивность контроля хранилищ носителей должна быть тем больше, чем выше степень угрозы хищения носителей, находящихся в хранилище. Степень угрозы хищения в свою очередь зависит от надежности: защиты территории, на которой расположены хранилища (НТ); защиты помещений, в которых находятся хранилища (НП); замков на дверях хранилищ (НЗ); библиотекарей хранилищ (НБ). Если для интенсивности контроля хранилищ носителей и для каждого из названных четырех параметров, влияющих на эту интенсивность, принять три возможных значения (малая (М), средняя (С), большая (Б)), то нечеткий алгоритм решения рассматриваемой задачи может быть представлен так, как показано на рис. 2.1.

Нетрудно видеть, что аппарат нестрогой математики может быть рекомендован для использования в таких ситуациях, в которых строгое описание систем и процессов их функционирования или невозможно или нецелесообразно в силу самого характера решаемой задачи. Так, в настоящее время нет необходимых данных для строгого определения значений параметров, определяющих степень уязвимости информации в КИС, эффективность систем защиты информации и т.п.

Вполне реальными являются также такие условия, когда строго количественные алгоритмы оценки ситуации и принятия решений являются нецелесообразными и даже вредными. Например, вряд ли целесообразно (по крайней мере, в настоящее время) пытаться строить строгий алгоритм для обеспечения выработки общей стратегии защиты информации. Построение такого алгоритма сопряжено с трудностями, преодоление которых неизбежно требует таких допущений, что адекватность этих алгоритмов становится весьма сомнительной. В то же время на основе чисто интуитивных рассуждений квалифицированных и опытных специалистов можно построить нечеткие (в указанном выше смысле) алгоритмы, которые, с одной стороны, будут достаточно простыми и адекватными реальным процессам, а с другой - создавать хорошие предпосылки для эффективного решения важных задач.

Нецелесообразность построения строгих алгоритмов может иметь место, например, в следующих ситуациях: реализация строгого алгоритма является трудоемкой, а время на его реализацию крайне ограничено; множество возможных ситуаций слишком велико, а возможности для их рассмотрения ограничены; поступающая информация такого качества, что результаты реализации строгого алгоритма являются сомнительными и т.п. В таких ситуациях, очевидно, целесообразным будет построение некоторых обобщенных алгоритмов, которые создадут предпосылки для наиболее рационального принятия решений в потенциально возможных ситуациях.

Именно такие подходы будут здесь использованы при обосновании рациональной технологии управления защитой информации, организации работ по защите информации и др.

Необходимо, однако, обратить внимание на следующее обстоятельство. При изложении вопросов практического использования методов нестрогой математики каждый раз акцентировалось внимание на том, что эти методы лишь создают предпосылки, необходимые для эффективного решения сооветствующей задачи, но не гарантируют эффективного решения. Такая гарантия может быть обеспечена лишь рациональными действиями людей, использующих нечеткие алгоритмы. Отсюда следует, что организация функционирования систем с высоким уровнем неопределенности должна включать в себя (и притом в качестве важнейшего атрибута) подготовку людей (персонала) к решению соответствующих задач с использованием методов нестрогой математики.

Вход

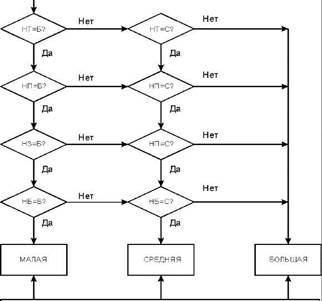
ИНТЕНСИВНОСТЬ КОНТРОЛЯ ХРАНИЛИЩ НОСИТЕЛЕЙ

Рис. 2.1. Структура нечеткого алгоритма определения интенсивности контроля хранилищ носителей

И, наконец, о соотношении методологии нестрогой математики и методологии теории нечетких множеств. При внимательном рассмотрении обеих названных методологий нетрудно усмотреть достаточно глубокую их аналогию. Объективным основанием для этого является то обстоятельство, что в основе обеих методологий лежит представление о неопределенности, размытости границ принадлежности элементов (представлений, суждений) определенному множеству. Однако существуют и принципиальные различия рассматриваемых методологий. В теории нечетких множеств, во-первых, предусматривается количественная оценка меры принадлежности рассматриваемых элементов тому или иному множеству, а во-вторых, предполагается разработка строгого алгоритма решения соответствующей задачи. В нестрогой математике нечеткость рассуждений последовательно проводится вплоть до алгоритма решения соответствующей задачи.