 |
Двухуровневое согласование линейных систем
|
|
|
|
Рассмотрим большую линейную стационарную систему:
(4.3.14)
Система может быть декомпозирована как:
(4.3.15)
где вектор взаимодействия (k x l), записанный как:
(4.3.16)
это линейная комбинация состояний N-1 подсистем, и Gij – это матрица ni x nj. Первоначальная задача оптимального управления системой сводится к оптимизации N подсистем, которые удовлетворяют (4.3.15)-(4.3.16) и минимизируют:
(4.3.17)
где Qi – это неотрицательно определенная матрица ni x ni, Ri и Vi – это положительно определенные матрицы mi x mi и ki x ki, где
(4.3.18)
Физическая интерпретация последнего слагаемого в интеграле (4.3.17) – это неточность в данной точке. Фактически, определяя это слагаемое, как будет видно дальше, мы избегаем выраженных управлений. «Согласование цели» и «баланс взаимодействия» использованные у Mesarvic и др. (1970), так же известны как задача «linear-quadratic» у Pearson (1971) и передача у Singh (1980) и Jamshidi (1983).
В этой декомпозиции большой взаимосвязанной линейной системы общие коэффициенты связи между ее N подсистемами – это переменная взаимосвязи zi(t), которые, вместе с (4.3.15)-(4.3.16), образуют ограничение связи. Эта формулировка называется глобальной и обозначается SG. Можно сделать следующее допущение. Глобальная проблема SG заменяется группой N подзадач, соединенных вместе через вектор параметров a=(a1,…,aN) и обозначенных si(a), i=1,…,N. Другими словами, глобальная системная задача SG включена в группу подсистемных проблем si(a) через внутренний параметр (Sandell и др., 1978) таким образом, что для определенного значения a*, подсистемы Si(a*), и i=1,…,N, дают желаемое решение для SG. Используя обозначения иерархического управления, эта внутренняя идея это и есть понятие согласования, но используя терминологию математического программирования задач, она называется основной проблемой (Geoffrion, 1970). На рисунке 4.6 изображена двухуровневая структура управления большой системой. Под этой стратегией, на i-й итерации каждый местный контроллер i получает 
от координатора (второй уровень иерархии), решает 
и передает (сообщает) некоторую функцию 
этого решения координатору.
|
|
|
Координатор, в свою очередь, оценивает следующее значение 
, т.е.:
(4.3.19)
где ei – это l-й размер шага итерации, и новый компонент dl, как мы вскоре увидим, часто берется за функцию ошибка взаимодействия:
(4.3.20)
Внутреннюю переменную взаимодействия zi(*) в (4.3.20) можно считать частью управляющей переменной доступной для контроллера i, в этом случае вектор параметра a(t) является набором двойных переменных или множителем Лагранжа, который соответствует ограничениям уравнения взаимодействия (4.3.16). Фундаментальная идея, которая стоит за этим подходом должна преобразовать задачу поиска минимума первоначальной системы в более легкую задачу поиска максимума, решение которой можно получить посредством двухуровневой итеративной схемы. Которая обсуждалась выше.
Введем двойную функцию
(4.3.21)
к объекту (4.3.15), где Лагранжиан L(*) определен как:
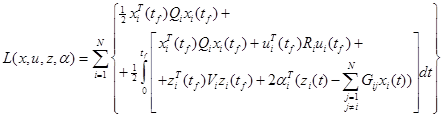(4.3.22)
где вектор параметра а состоит из k множителей Лагранжа. Таким образом, первоначально ограниченная (взаимодействием подсистем) оптимизационная задача превращается в неограниченную, другими словами ограничение (4.3.16) удовлетворяется через определение набора множителей Лагранжа ai, i=1,…,k. В таких случаях, когда функции ограничений выпуклые, теорема сильной двойственности Лагранжа (Geoffrion, 1971a, b; Singh, 1980) показывает, что
|
|
|
(4.3.23)
определяя, что минимизация J в (4.3.17) для объекта (4.3.15)-(4.3.16) эквивалентна максимуму двойной функции q(a) в (4.3.21) по параметру a. Чтобы облегчить решение этой задачи, замечено, что для определенного набора этих множителей Лагранжа а=а*, Лагранжиан можно переписать в виде:
(4.3.24)
который обнаруживает, что декомпозицию применяют к Лагранжиану таким образом, что, подлагранжиан Li существует для каждой подсистемы. Каждая подсистема будет стремиться минимизировать свой собственный подлагранжиан Li, как определенно в (4.3.24) для объекта (4.3.15) и используя множители Лагранжа a*, которые считаются известными функциями на первом уровне иерархии. Результат каждой такой минимизации позволит определить двойственную функцию q(a*) в (4.3.21). На втором уровне, на котором решение всех подсистем первого уровня известны, значение q(a*) будет изменено типичной неограниченной оптимизацией, например метод Ньютона, градиента или скоростного градиента. Градиентные методы используются потому, что градиент q(a) определяется:
(4.3.25)
это ошибки взаимодействия подсистем, которые известны из решений первого уровня и 
определяет градиент f по х. На втором уровне вектор a изменяется по формуле (4.3.19) и рисунку 4.6. Если применяется градиентный метод (с крутым склоном), вектор dl в (4.3.19) является просто l-й итеративной ошибкой взаимодействия el(t). Однако, для повышения точности вычислений определим скоростной градиент как:
(4.3.26)
где
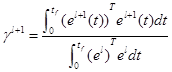(4.3.27)
и d0=e0. Как только вектор ошибки e(t) достигает нуля, появляется оптимальное иерархическое управление s. Ниже дана пошаговая процедура вычисления для метода согласования цели иерархического управления.
Алгоритм 4.1. Метод согласования цели.
Шаг 1. Для каждой подсистемы первого уровня, минимизируем каждый подлагранжиан Li, используя известный множитель Лагранжа a=a*, так как подсистемы линейные, может быть использовано уравнение Риккати. Сохраним решение. (Читатели не знакомые с уравнением Риккати могут прочитать раздел 4.3.2, метод прогнозирования взаимодействия).
|
|
|
Шаг 2. На втором уровне используется итеративный метод скоростного градиента, похожий на (4.3.26)-(4.3.27), чтобы изменить траектории a*(t) как в (4.3.19). Как только общая ошибка взаимодействия системы будет нормализована из
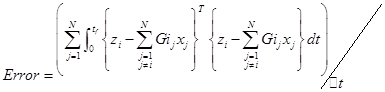(4.3.28)
и будет достаточно мала, будет достигнуто оптимальное решение для системы. Здесь 
– размер шага интегрирования.
Два примера ниже иллюстрируют метод согласования цели или баланса взаимодействия. Первый пример, который был предложен Pearson (1971), и позже рассмотрен Singh (1980) и Jamshidi (1983), использован в изменненой форме. Второй пример показывает модель многоколенной задачи загрязнения реки (Beck, 1974; Singh, 1975). Полная оценка многоуровневых методов дана в секции 4.6, а описание нелинейных многоуровневых нелинейных систем в главе 6. Две альтернативы решения этого иерархического управления основаны на расширенных рядах Тейлора и Чебышева в разделе 4.6.
Пример 4.3.1. Рассмотрим систему 12-го порядка введенную Pearson (1971) и показанную на рис 4.7 с уравнением состояния:
(4.3.29)
и квадратичной функцией оценки:
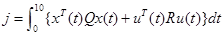(4.3.30)
с
где
Вектор выхода системы представлен как:
(4.3.31)
Необходимо найти стратегию иерархического управления по методу баланса взаимодействий (согласования цели).
Решение: Из схемы системы, показанной на рисунке 4.7 (пунктирные линии) и матрицы состояния (4.3.29) ясно, что есть четыре подсистемы третьего порядка соединенных через шесть ограничивающих уравнений (по числу пунктирных линий на рис. 4.7):
(4.3.32)
где ei, i=1,…,6 представляет ошибки взаимодействия между четырех подсистемами. Задачи подсистем первого уровня были решены через набор из четырех матричных уравнений Риккати третьего порядка:
(4.3.33)
где Ki(t) – это положительно определенная матрица Риккати ni x ni и 
. Методы «без взаимодействия» и «удвоения» решают дифференциальное матричное уравнение Риккати, предложены Davison и Maki в 1973 и рассмотрены Jamshidi в 1980,были использованы для компьютерного решения (4.3.33). Уравнения состояния подсистем были решены стандартным методом Рунге-Кутта четвертого порядка, а итерации второго уровня были выполнены по схеме скоростного градиента (4.3.19), (4.3.26)-(4.3.27), используя кубическую сплайн интерполяцию (Hewlett-Packard, 1979) для оценки подходящих численных интегралов. Размер шага был выбран 
=0.1, как и в более ранних рассмотрениях этого примера (Pearson, 1971; Singh, 1980). Алгоритм скоростного градиента позволил уменьшить ошибку с 1 до 
за шесть итераций, как показано на рисунке 4.8, который был в тесной связи с результатами предыдущих исследований модифицированной версии системы (4.3.29), полученными Singh (1980). Рассмотрим второй пример.
|
|
|
Пример 4.3.2. Рассмотрим двухколенную модель задачи управления загрязнением реки.
(4.3.34)
где каждое колено (подсистема) реки имеет два состояния – x1 – это концентрация биохимической потребности в кислороде (БПК) (биохимическая потребность в кислороде представляет собой уровень содержания кислорода полученного в результате распада органического вещества) и х2 – это концентрация растворенного кислорода (РК) – и управление u1 – это БПК вод втекающих в реку. Для квадратичной функции оценки
(4.3.35)
С Q=diag(2,4,2,4) и R=diag(2,2), необходимо найти оптимальное управление, которое оптимизирует (4.3.35) для объекта (4.3.34) при x(0)=(11 -11)T.
Решение: Как видно из (4.3.34)-(4.3.35), две задачи первого уровня идентичны, и матричное уравнение Риккати второго порядка решается интегрированием (4.3.33) используя метод Рунге-Кутта четвертого порядка при =0.1. Ошибка взаимодействия в этом примере снижена до 
за 15 итераций, как показано на рисунке 4.9. Оптимальные концентрации БПК и РК двух колен реки показаны на рисунке 4.10.
|
|
|
