 |
Согласование цели и однородность
|
|
|
|
Когда в (4.3.15) – (4.3.17) обсуждался метод согласования цели, было замечено, что положительно определенные матрицы Si были введены в функцию оценки (4.3.17) для того, чтобы избежать однородности. Чтобы убедится в этом, обратимся к задаче минимизации Li в (4.1.24) для объекта (4.3.15). Пусть i-й Гамильтониан подсистемы имеет вид:
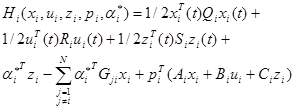(4.3.62)
Одно из необходимых уравнений для решения задачи i-й подсистемы на первом уровне
(4.3.63)
или
(4.3.64)
где однородное решение появляется, если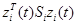 
не появляется в функции оценки. Чтобы избежать однородности на первом уровне возможны два альтернативных подхода. Следующий пример иллюстрирует два подхода.
Пример 4.3.5. Рассмотри следующую систему:
(4.3.65)
Необходимо найти (u1,u2), такие, чтобы они удовлетворяли (4.3.65), а квадратичная функция оценки
(4.3.66)
минимизировалась методом согласования цели.
Решение: Из (4.3.65) –(4.3.66) ясно, что систему можно разделить на две подсистемы первого порядка.
(4.3.67)
(4.3.68)
с ограничением взаимодействия
(4.3.69)
Задача в настоящий момент имеет следующий Гамильтониан:
(4.3.70)
в котором переменная взаимодействия появляется линейно. Применение метода согласования цели для данной формулировки приведет к однородности, так как z1 появляется линейно в (4.3.70). Следующая системная переформулировка задач поможет избежать однородности.
|
|
|
Часть а – подсистема 1, переменные состояния
Часть б – подсистема 1, переменные управления
Часть в – подсистема 2, переменные состояния
Часть г – подсистема 2, переменные управления
А. Переформулировка 1.
Bauman (1968) предложил переписать ограничения взаимодействия квадратичной формы
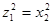(4.3.71)
которая даст следующее необходимое условие для оптимизации на первом уровне:
(4.3.72)
для первой подсистемы и
(4.3.73)
для второй подсистемы. После введения формулы Риккати (4.3.72) и (4.3.73) мы получим:
и
где ki(t) – i-я скалярная нестационарная матрица Риккати для подсистемы. Согласование на втором уровне достигается через следующие итерации:
Эта переформулировка помогает избежать однородности, но делает схождение итераций второго уровня очень медленным.
Б. Переформулировка 2.
Singh (1980) предложил альтернативную формулировку, которая не только позволит избежать однородности, но и даст хорошее схождение процедура основывается на том, чтобы найти х через вектор взаимодействия z и подставить его в функцию оценки, т.е. z можно представить как:
где G – считается неоднородной и переформулированный Гамильтониан представлен в виде:
В этом примере матрица G – однородна, но решение можно получить. Гамильтониан имеет вид:
А задача подсистемы первого уровня имеет вид
и
вторую подсистему можно решить сразу же, так как уравнение p2 – косостояние отделено от х2 и может быть решено в обратном порядке и подставлено в уравнение х2, что приведет к тому, что решение уравнения Риккати в данном примере не требуется. Но для первой подсистемы, исходя из формулировки задач первого уровня в прогнозировании взаимодействия (4.3.40) – (4.3.51), необходимо как уравнение Риккати, так и открытое сопряженное (компенсирующее) векторное уравнение. Для этого примера задача первой подсистемы имеет вид
|
|
|
где два дифференциальных уравнения для ki(t) и gi(t) нужно решить в обратном порядке. В то время как для второй подсистемы не нужно решать вспомогательное уравнение, надо решить два таких уравнения для первой подсистемы. В общем эта переформулировка требует решения
(4.3.74)
что означает, что уравнения вектора косостояния p отделено от х и может быть решено в обратном порядке (без решения уравнения Риккати) и подставлено в верхнее уравнение для нахождения х. Так как матрицы A, B, Q и R – блок-диагональные, задачу (4.3.74) можно разделить на N задач подсистем с условием, что 
отделяемо от z, где V=G-1.
|
|
|
