 |
Метод прогнозирования взаимодействия.
|
|
|
|
Альтернативный подход к оптимальному управлению иерархическими системами, который имеет как открытый, так и закрытый контур управления, - это метод прогнозирования взаимодействия, который основывается на работе Takahara (1965), который избегает упоминания о градиентных итерациях второго уровня. Рассмотрим большую линейную взаимосвязанную систему, которая декомпозирована на N подсистем, каждая из которых может быть описана
(4.3.36)
Где вектор взаимодействия zi:
(4.3.37)
Задача оптимального управления на первом уровне – найти управление ui(t), которое удовлетворяет (4.3.36)-(4.3.37), минимизируя обычную квадратичную функцию оценки:
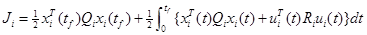(4.3.38)
Эту задачу можно решить введением множества множителей Лагранжа ai(t), и векторов косостояния pi(t), чтобы увеличить ограничение уравнения взаимодействия (4.3.37) и подсистем динамического ограничения (4.3.36) до подынтегральной функции оценки, т.е. Гамильтониан i-й подсистемы будет определен как:
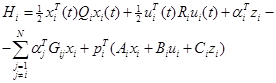(4.3.39)
Затем должно быть написано несколько необходимых условий:
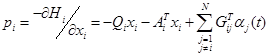(4.3.40)
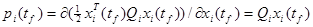(4.3.41)
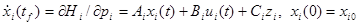(4.3.42)
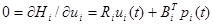(4.3.43)
где векторы ai(t) и zi(t) – уже не считаются неизвестными на первом уровне, и фактически ai(t) увеличивает zi(t), чтобы образовать широкоразмерный вектор согласования, который мы рассмотрим ниже. Для решения задачи первого уровня, надо принять 
как известную. Замете, что ui(t) можно выделить из (4.3.43):
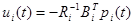(4.3.44)
|
|
|
и подставить в (4.3.40)-(4.3.42), получив:
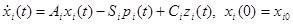(4.3.45)
(4.3.46)
который образует линейную двухточечную краевую (ДТК) задачу, и, как в (4.3.33)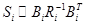 
. Можно увидеть, что ДТК задача может быть разложена введением матрицы Риккати. Это выглядит как:
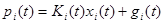(4.3.47)
где gi(t) – это разомкнутый сопряженный или компенсирующий вектор, размерностью ni. Если обе части уравнения (4.3.47) продифференцированы 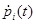и 
и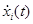 
из (4.3.46) и (4.3.45) подставлены в него, можно вновь использовать (4.3.47) и уравнительные коэффициенты для первого и нулевого порядка xi(t), получив следующие матричные и векторные дифференциальные уравнения:
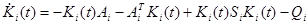(4.3.48)
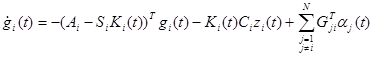(4.3.49)
где конечные условия Ki(tf) и gi(tf) вытекают из (4.3.41) и (4.3.47).
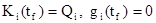(4.3.50)
В результате данного уравнения оптимальное уравнение первого уровня становится
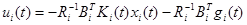(4.3.51)
который имеет частичную закрытую обратную связь и прямую (открытую) обратную связь. Можно сделать два вывода. Первый, решение дифференциального, симметричного матричного уравнения Риккати, в которое включены ni(ni+1)/2 нелинейных скалярных уравнений не зависит от первоначального состояния xi(0). Второй, в отличие от Ki(t), gi(t) в (4.3.49) посредством zi(t) зависит от xi(0). Это свойство будет использовано в разделе 4.4, чтобы получить абсолютно закрытое управление в иерархической структуре.
Задача второго уровня сильно изменяет новый вектор согласования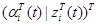 
. Для этой цели определите аддитивно отделяемый Лагранжиан:
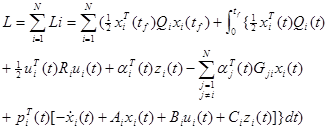(4.3.52)
Значение ai(t) и zi(t) можно получить из:
(4.3.53)
(4.3.54)
т.е.:
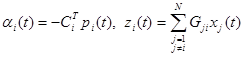(4.3.55)
Процедура согласования второго уровня на итерации (l+1) имеет вид:
|
|
|
(4.3.56)
Метод прогнозирования взаимодействия формулируется следующим алгоритмом:
Алгоритм 4.2 Метод прогнозирования взаимодействия для непрерывных систем:
Шаг 1. Решить N независимых дифференциальных матричных уравнений Риккати (4.3.48) с конечным условием (4.3.50) и сохраните Ki(t), i=1,2…,N. Инициализируйте ai(t) случайными числами и найдите соответствующее значение для zi(t).
Шаг 2. На l-й итерации используйте значения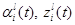 
чтобы решить сопряженное уравнение (4.3.49), с конечным условием (4.3.50). Сохраните gi(t), i=1,2,…,N.
Шаг 3. Решите уравнение состояния
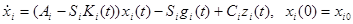(4.3.57)
И сохраните xi(t), i=1,2,…,N.
Шаг 4. На втором уровне используйте результаты шагов 2 и 3 и (4.3.56) чтобы изменить согласующий вектор:
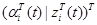
Шаг 5. Проверьте сходимость на втором уровне, оценив общую ошибку взаимодействия:
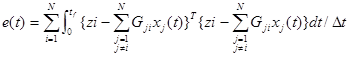(4.3.58)
Шаг 6. Если необходимая сходимость достигнута – остановитесь. Иначе, установите l=l+1 и перейдите к шагу 2.
Важно отметить, что в зависимости от типа цифрового компьютера, и его операционной системы, расчеты подсистем могут осуществляться параллельно, а также N-матричное уравнение Риккати на шаге 1 не зависит от xi(0), и значит их необходимо вычислить один раз, не зависимо от числа итераций второго уровня в алгоритме прогнозирования взаимодействия (4.3.56). В отличие от методов согласования цели, zi(t) не нужен в функции оценки, который был необходим, чтобы избежать однородности, о чем будет написано в следующем разделе.
Метод прогнозирования взаимодействия, введенный Tokahara (1965), был рассмотрен многими исследователями, которые внесли в него существенный вклад. Среди них Titli (1972) который назвал этот метод смешанным (Singh, 1980) и Cohen и др. (1974), который предоставил более убедительные доказательства сходимости чем предложенные ранее. Smith и Sage (1973) рассмотрели эту схему для нелинейных систем, которая будет рассмотрена в Главе 6. Сравнение методов прогнозирования взаимодействия, согласования цели и подходов без интеграции, рассмотренных в разделе 4.4, дано в разделе 4.5. Следующие два примера, а потом пример в САПР иллюстрирует метод прогнозирования взаимодействий.
Пример 4.3.3. Рассмотрим систему четвертого порядка
|
|
|
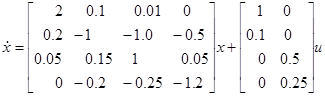(4.3.59)
Где x(0)=(-1,0.1,1.0,-0.5)T, квадратичная функция оценки Q=daig(2,1,1,2), R=diag(1,2) и нет граничного штрафа. Надо использовать метод прогнозирования взаимодействия и найти оптимальное управление для tf =1.
Решение: Систему разделили на две подсистемы второго порядка и применили методы, описанные в алгоритме 4.2. На первом шаге решили два независимых дифференциальных матричных уравнения Риккати используя как дублирующий алгоритм Davison и Maki (1973), так и стандартный метод Рунге-Кутта. Элементы матрицы Риккати были представлены в виде квадратичного полинома в ряде Чебышева (Newhouse,1962), для удобства вычислений:
(4.3.60)
На первом уровне были решены два сопряженных уравнения второго порядка в виде (4.3.49) и два уравнения состояния подсистем, как показано в алгоритме 4.2 в шаге 3, используя метод четвертого порядка Рунге-Кутта и первоначальные значения
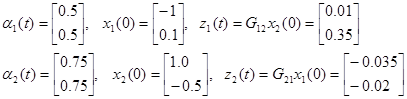(4.3.61)
На втором уровне векторы взаимодействия [a11(t),a12(t),z11(t),z12(t)] и [a21(t),a22(t),z21(t),z22(t)]T были спрогнозированы с использованием рекурсивных отношений (4.3.56), и на каждой итерации производился обмен информацией с подсчетом общей ошибки взаимодействия (4.3.58) для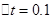 
и программы кубической сплайн интерполяции. Ошибку взаимодействия снизили до 
за шесть итераций, как показано на рисунке 4.11. Были получены оптимальные значения выхода для Ci =(1 1) и сигнала управления. Затем для сравнения первоначальную систему (4.3.59) оптимизировали, решив нестационарное матричное уравнение Риккати четвертого порядка обратным интегрированием, и для хi(t), i=1,2,3,4; yj(t) и uj(t), j=1,2. Значения выхода и сигналы управления как для случая иерархического управления, так и для централизованного, показаны на рисунке 4.12. Отметьте относительно точное соответствие между значениями выхода для первоначальной соединенной и иерархической разъединенной систем. Но как и ожидалось, эти два уравнения различны.
Теперь рассмотрим второй пример.
Пример 4.3.4. Рассмотрим систему восьмого порядка
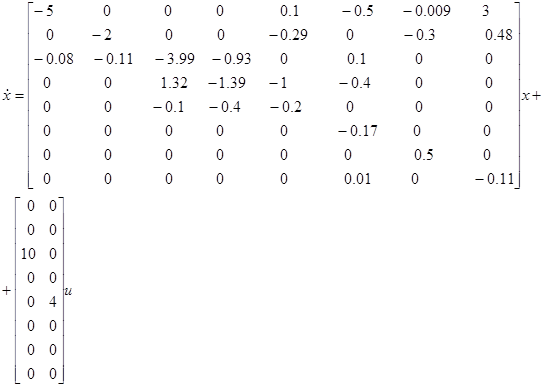
Необходимо использовать метод прогнозирования взаимодействия для нахождения u*.
|
|
|
Решение: Система была разложена на две подсистемы четвертого порядка и были выбраны tf=2, 
=0.1, Q1=Q2=I4, R1=R2=1. Первоначальные значения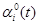 
, i=1,2 и состояние х0 были приняты за 
, 
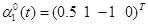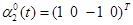и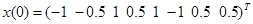 
. Сходимость была очень быстрой, как видно на рисунке 4.13. Всего за четыре итерации второго уровня ошибка взаимодействия была снижена до 
. Фактически была быстрая сходимость для различных x0 и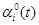 
.
САПР пример 4.3.1. Рассмотрим систему четвертого порядка в примере 4.3.1 в (4.3.59):
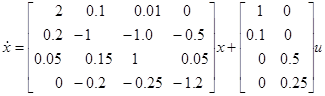
Где x(0)=(-1,0.1,1.0,-0.5)T, квадратичная функция оценки Q =diag(2,1,1,2), R=diag(1,2) и нет граничного штрафа. Необходимо использовать LSSPAK или подобное программное обеспечение и метод прогнозирования взаимодействия и найти оптимальное управление для tf=2.
Решение: Как и раньше, система делится на две подсистемы второго порядка, и уравнения Риккати для подсистем решаются с использованием RICRKUT от LSSPAK/PC, а их решения представлены в виде полинома четвертого порядка для удобства вычислений. Используя программу INTRPRD от LSSPAK/PC реализуют алгоритм прогнозирования взаимодействия и схождение достигается за пять итераций. Точные выборки из выполнения этого САПр примера приведены ниже. Инструкции для вычерчивания программы прогнозирования взаимодействия появляются, когда на экране появится чертеж; нажмите Enter, чтобы вернуться к меню.
Если вы хотите вывести чертежи через принтер откройте DOS файл GRAPHICS до запуска программы, когда вы захотите вывести чертеж, нажмите shift-PrtScr.
Optimization via the interaction prediction method.
Initial time (to): 0
Final time (tf): 2
Step size (Dt):.1
Total no. of 2nd level iterations = 6
Error tolerance for multi-level iterations -.00001
Order of overall large scale system = 4
Order of overall control vector (r) = 2
Number of subsystems in large scale system = 2
Matrix Subsystem state orders-n sub i 0.200D+01 0.200D+01
Matrix Subsystem input orders-r sub i 0.100D+01 0.100D+01
Polynomial approximation for the Ricatti matrices to be used.
Matrix Ricatti coefficients for SS# 1
| 0.453D+01 | -.259D+01 | 0.794D+01 | -762D+01 | O.186D+01 |
| 0.978D-01 | -.793D-01 | 0.252D+00 | .233D+00 | 0.571D-01 |
| 0.490D+00 | 0.759D-02 | -.109D+00 | 0.975D-01 | -.531D-01 |
Matrix Ricatti coefficients for SS# 2
| 0.112D+01 | -.815D+01 | 0.361D+01 | 0.455D+01 | 0.105D+01 |
| -0.149D+00 | -.322D-01 | 0.697D-01 | .284D-01 | 0.183D-01 |
| 0.815D+00 | 0.642D-01 | -.295D+00 | 0.305D+00 | -.138D+00 |
System Matrix A
| 0.200D+01 | 0.100D+00 | 0.100D-01 | 0.000D+00 |
| 0.200D+00 | 0.100D+01 | 0.100D+00 | 0.500D+00 |
| 0.500D-01 | 0.150D+00 | 0.100D+01 | 0.500D-01 |
| 0.000D+00 | -0.200D+00 | 0.250D+00 | -0.120D+01 |
Matrix Input Matrix B
| 0.100D+01 | O.OOOD+00 |
| 0.100D+00 | O.OOOD+00 |
| O.OOOD+00 | O.250D+O0 |
Matrix Input Cost Function R
| 0.100D+01 | O.OOOD+OO |
| 0.000D+O0 | 0.200D+01 |
Matrix Lagrange Multiplier Initial Values
| 0.100D+01 |
| O.IOOD+Ol |
| 0.100D+01 |
| 0.100D+01 |
Matrix Initial conditions vector xO
| -.100D+01 |
| 0.100D+00 |
| 0.100D+01 |
| -.500D+00 |
Subsystem no. 1 at 2nd level iteration no. 1
Subsystem no. 2 at 2nd level iteration no. 1
At second level iteration no. 1 interaction error = 0.347D+00
Subsystem no. 1 at 2nd level iteration no. 2
Subsystem no. 2 at 2nd level iteration no. 2
At second level iteration no. 2 interaction error = 0.771D - 03
Subsystem no. 1 at 2nd level iteration no. 3
Subsystem no. 2 at 2nd level iteration no. 3
|
|
|
At second level iteration no. 3 interaction error = 0.507D - 03
Subsystem no. 1 at 2nd level iteration no. 4
Subsystem no. 2 at 2nd level iteration no. 4
At second level iteration no. 4 interaction error = 0.323D - 04
Subsystem no. 1 at 2nd level iteration no. 5
Subsystem no. 2 at 2nd level iteration no. 5
At second level iteration no. 5 interaction error = 0.310D - 05
Оптимальные отклики показаны на рисунке 4.14, а схождение на рисунке 4.15.
Другие применения метода прогнозирования взаимодействия представлены в разделе задач.
|
|
|
