 |
Самостоятельные задания по теме
|
|
|
|
Для изучения вкладов населения в коммерческом банке города была проведена 5%-я случайная выборка лицевых счетов, в результате которой получено следующее распределение клиентов по размеру вкладов:
| Размер вклада, у.е. | Число вкладчиков, чел. | |||||||||
| Вариант | ||||||||||
| до 5000 | ||||||||||
| 5 000 – 15 000 | ||||||||||
| 15 000 – 30 000 | ||||||||||
| 30 000 – 50 000 | ||||||||||
| свыше 50 000 |
С вероятностью 0,954 определить:
1) средний размер вклада во всем банке;
2) долю вкладчиков во всем банке с размером вклада свыше 15000 у.е.;
3) необходимую численность выборки при определении среднего размера вклада, чтобы не ошибиться более чем на 500 у.е.;
4) необходимую численность выборки при определении доли вкладчиков во всем банке с размером вклада свыше 30 000 у.е., чтобы не ошибиться более чем на 10%.
Тема 4. Ряды динамики
Методические указания по теме
Задача 1. Смертность от болезней системы кровообращения в России за период гг. характеризуется следующим рядом динамики.
| Год | ||||||||||
| Умершие, тыс. чел. | 1163,5 | 1113,7 | 1100,3 | 1094,1 | 1187,8 | 1231,4 | 1253,1 | 1308,1 | 1330,5 | 1287,7 |
Вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Проверить ряд на наличие в нем линейного тренда, на основе которого рассчитать интервальный прогноз на год с вероятностью 95%.
Решение. Любое изменение уровней ряда динамики определяется базисным (сравнение с первым уровнем) и цепным (сравнение с предыдущим уровнем) способами. Оно может быть абсолютным (разность уровней ряда) и относительным (соотношение уровней).
|
|
|
Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда (47), а цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда (48).
 (47)
(47)  (48)
(48)
По знаку абсолютного изменения делается вывод о характере развития явления: при  > 0 — рост, при
> 0 — рост, при  < 0 — спад, при
< 0 — спад, при  = 0 — стабильность.
= 0 — стабильность.
В нашей задаче эти изменения определены в 3-м и 4-м столбцах таблицы 5. Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений равняется последнему базисному. В нашей задаче это правило выполняется:  = 124,2 и
= 124,2 и  = 124,2.
= 124,2.
Базисное относительное изменение представляет собой соотношение конкретного и первого уровней ряда (49), а цепное относительное изменение представляет собой соотношение конкретного и предыдущего уровней ряда (50).
 (49)
(49)  (50)
(50)
Относительные изменения уровней — это по существу индексы динамики, критериальным значением которых служит 1. Если они больше ее, имеет место рост явления, меньше ее — спад, а при равенстве единице наблюдается стабильность явления.
В нашей задаче эти изменения определены в 5-м и 6-м столбцах таблицы 5.
Вычитая единицу из относительных изменений, получают темп изменения уровней, критериальным значением которого служит 0. При положительном темпе изменения имеет место рост явления, при отрицательном — спад, а при нулевом темпе изменения наблюдается стабильность явления. В нашей задаче темпы изменения определены в 7-м и 9-м столбцах таблицы 5, а в 8-м и 10-м сделан вывод о характере развития изучаемого явления. Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему базисному. В нашей задаче это правило выполняется:  =1,107 и
=1,107 и  =1,107.
=1,107.
|
|
|
Таблица 5. Вспомогательные расчеты для решения задачи

Обобщенной характеристикой ряда динамики является средний уровень ряда  . Способ расчета
. Способ расчета  зависит от того, моментный ряд или интервальный (см. рис.3):
зависит от того, моментный ряд или интервальный (см. рис.3):

Рис.3. Методы расчета среднего уровня ряда динамики.
В нашей задаче ряд динамики интервальный, значит, применяем формулу средней арифметической простой (17):  = 12070,2 / 10 = 1207,02 (тыс. чел.). То есть за период 1995-2004 в России в среднем за год от болезней системы кровообращения умирало 1207,02 тыс. чел.
= 12070,2 / 10 = 1207,02 (тыс. чел.). То есть за период 1995-2004 в России в среднем за год от болезней системы кровообращения умирало 1207,02 тыс. чел.
Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.
Базисное среднее абсолютное изменение – это частное от деления последнего базисного абсолютного изменения на количество изменений уровней (51). Цепное среднее абсолютное изменение уровней ряда – это частное от деления суммы всех цепных абсолютных изменений наколичество изменений (52).
 Б =
Б =  (51)
(51)  Ц =
Ц =  (52)
(52)
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными. В нашей задаче  = 124,2/9 = 13,8, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 13,8 тыс. чел.
= 124,2/9 = 13,8, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 13,8 тыс. чел.
Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение определяется по формуле (53), а цепное среднее относительное изменение – по формуле (54):
 Б=
Б=  =
=  (53)
(53)  Ц=
Ц=  (54)
(54)
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашей задаче  =
=  = 1,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет в 1,0114 раза.
= 1,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет в 1,0114 раза.
Вычитанием 1 из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашей задаче  = 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%.
= 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%.
|
|
|
Проверка ряда динамики на наличие в нем тренда (тенденции развития ряда) возможна несколькими способами (метод средних, Фостера и Стюарта, Валлиса и Мура и пр.), но наиболее простым является графическая модель, где на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально. Тренд может представлять собой прямую линию, параболу, гиперболу и т.п. В итоге приходим к трендовой модели вида:
 , (55)
, (55)
где 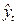 – математическая функция развития;
– математическая функция развития;  – случайное или циклическое отклонение от функции; t – время в виде номера периода (уровня ряда). Цель такого метода – выбор теоретической зависимости
– случайное или циклическое отклонение от функции; t – время в виде номера периода (уровня ряда). Цель такого метода – выбор теоретической зависимости  в качестве одной из функций:
в качестве одной из функций:
 – прямая линия;
– прямая линия;  – гипербола;
– гипербола;  – парабола;
– парабола;  – степенная;
– степенная;  – ряд Фурье.
– ряд Фурье.
.
Определение параметров  в этих функциях может вестись несколькими способами, но самые незначительные отклонения аналитических (теоретических) уровней (
в этих функциях может вестись несколькими способами, но самые незначительные отклонения аналитических (теоретических) уровней ( – читается как «игрек, выравненный по t») от фактических (
– читается как «игрек, выравненный по t») от фактических ( ) дает метод наименьших квадратов – МНК. При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней
) дает метод наименьших квадратов – МНК. При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней  от теоретических уровней
от теоретических уровней  :
:
 . (56)
. (56)
В нашей задаче при выравнивании по прямой вида  параметры
параметры  и
и  отыскиваются по МНК следующим образом. В формуле (55) вместо
отыскиваются по МНК следующим образом. В формуле (55) вместо  записываем его конкретное выражение
записываем его конкретное выражение  . Тогда
. Тогда  . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении
. Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении  и
и  функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по
функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по  и
и  , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным найдем частные производные:

Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:
|
|
|
 (57)
(57)
где n – количество уровней ряда; t – порядковый номер в условном обозначении периода или момента времени; y – уровни эмпирического ряда.
Эта система и, соответственно, расчет параметров  и
и  упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала:
упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала:  ,
,  ,
,  и т.д.
и т.д.
При таком порядке отсчета времени (от середины ряда)  = 0, поэтому, система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
= 0, поэтому, система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
 (58)
(58)
Как видим, при такой нумерации периодов параметр  представляет собой средний уровень ряда. Определим по формуле (58) параметры уравнения прямой, для чего исходные данные и все расчеты необходимых сумм представим в таблице 6.
представляет собой средний уровень ряда. Определим по формуле (58) параметры уравнения прямой, для чего исходные данные и все расчеты необходимых сумм представим в таблице 6.
Из таблицы получаем, что  = 12070,2/10 = 1207,02 и
= 12070,2/10 = 1207,02 и  = 4195/330 = 12,7121. Отсюда искомое уравнение тренда
= 4195/330 = 12,7121. Отсюда искомое уравнение тренда 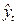 =1207,02+12,7121t. В 6-м столбце таблицы 6 приведены трендовые уровни, рассчитанные по этому уравнению
=1207,02+12,7121t. В 6-м столбце таблицы 6 приведены трендовые уровни, рассчитанные по этому уравнению
По полученной модели для каждого периода (каждой даты) определяются теоретические уровни тренда ( ) и оценивается надежность (адекватность) выбранной модели тренда. Оценку надежности проводят с помощью критерия Фишера, сравнивая его расчетное значение Fр с теоретическими значениями FТ (приложение 1). При этом расчетный критерий Фишера определяется по формуле:
) и оценивается надежность (адекватность) выбранной модели тренда. Оценку надежности проводят с помощью критерия Фишера, сравнивая его расчетное значение Fр с теоретическими значениями FТ (приложение 1). При этом расчетный критерий Фишера определяется по формуле:
 , (59)
, (59)
где k – число параметров (членов) выбранного уравнения тренда; ДА – аналитическая дисперсия, определяемая по формуле (61); До – остаточная дисперсия (62), определяемая как разность фактической дисперсии ДФ (60) и аналитической дисперсии:
 ; (60)
; (60)
 ; (61)
; (61)
 . (62)
. (62)
Сравнение расчетного и теоретического значений критерия Фишера ведется обычно при уровне значимости  с учетом степеней свободы
с учетом степеней свободы  и
и  . Уровень значимости
. Уровень значимости  связан с вероятностью
связан с вероятностью  следующей формулой
следующей формулой  . При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
. При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
Таблица 6. Вспомогательные расчеты для решения задачи
| Год | y | t | t2 | yt | 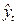
| (y – 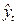 )2 )2
| (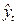 – –  )2 )2
| (y –  )2 )2
|
| 1163,5 | -9 | -10471,5 | 1092,611 | 5025,263 | 13089,44 | 1893,9904 | ||
| 1113,7 | -7 | -7795,9 | 1118,035 | 18,79354 | 7918,3033 | 8708,6224 | ||
| 1100,3 | -5 | -5501,5 | 1143,459 | 1862,733 | 4039,9506 | 11389,1584 | ||
| 1094,1 | -3 | -3282,3 | 1168,884 | 5592,592 | 1454,3822 | 12750,9264 | ||
| 1187,8 | -1 | -1187,8 | 1194,308 | 42,35249 | 161,59803 | 369,4084 | ||
| 1231,4 | 1231,4 | 1219,732 | 136,1394 | 161,59803 | 594,3844 | |||
| 1253,1 | 3759,3 | 1245,156 | 63,10136 | 1454,3822 | 2123,3664 | |||
| 1308,1 | 6540,5 | 1270,581 | 1407,705 | 4039,9506 | 10217,1664 | |||
| 1330,5 | 9313,5 | 1296,005 | 1189,915 | 7918,3033 | 15247,3104 | |||
| 1287,7 | 11589,3 | 1321,429 | 1137,652 | 13089,44 | 6509,2624 | |||
| Итого | 12070,2 | 12070,2 | 16476,25 | 53327,348 | 69803,596 |
Проверим тренд в нашей задаче на адекватность по формуле (59), для чего в 7-м столбце таблицы 6 рассчитан числитель остаточной дисперсии, а в 8-м столбце – числитель аналитической дисперсии. В формуле (59) можно использовать их числители, так как оба они делятся на число уровней n (n сократятся): FР = 53327,348*8/(16476,25*1) = 25,893 > FТ, значит, модель адекватна и ее можно использовать для прогнозирования (FТ = 5,32 находим по приложению 1 в 1-ом столбце [  = k – 1 = 1] и 8-й строке [
= k – 1 = 1] и 8-й строке [  = n – k = 8]).
= n – k = 8]).
|
|
|
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (63):
 , (63)
, (63)
где  – точечный прогноз, рассчитанный по модели тренда;
– точечный прогноз, рассчитанный по модели тренда;  – коэффициент доверия по распределению Стьюдента при уровне значимости
– коэффициент доверия по распределению Стьюдента при уровне значимости  и числе степеней свободы
и числе степеней свободы  =n–1 (приложение 2);
=n–1 (приложение 2); 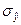 – ошибка аппроксимации, определяемая по формуле (64):
– ошибка аппроксимации, определяемая по формуле (64):
 , (64)
, (64)
где  и
и  – соответственно фактические и теоретические (трендовые) значения уровней ряда динамики; n – число уровней ряда; k – число параметров (членов) в уравнении тренда.
– соответственно фактические и теоретические (трендовые) значения уровней ряда динамики; n – число уровней ряда; k – число параметров (членов) в уравнении тренда.
Определим доверительный интервал в нашей задаче на 2005 год с уровнем значимости  = (1–0,95) = 0,05. Для этого найдем ошибку аппроксимации по формуле (64):
= (1–0,95) = 0,05. Для этого найдем ошибку аппроксимации по формуле (64): 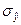 =
=  = 45,38. Коэффициент доверия по распределению Стьюдента
= 45,38. Коэффициент доверия по распределению Стьюдента  = 2,2622 при
= 2,2622 при  = 10 – 1=9.
= 10 – 1=9.
Прогноз на 2005 с вероятностью 95% осуществим по формуле (63):
Y2005 =(1207,02+12,7121*11) 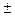 2,2622*45,38 или 1244,19< Y2005 <1449,51 (тыс.чел.).
2,2622*45,38 или 1244,19< Y2005 <1449,51 (тыс.чел.).
|
|
|


